2312-卖木头块
给你两个整数 m 和 n ,分别表示一块矩形木块的高和宽。同时给你一个二维整数数组 prices ,其中 prices[i] = [hi, wi, pricei] 表示你可以以 pricei 元的价格卖一块高为 hi 宽为 wi 的矩形木块。
每一次操作中,你必须按下述方式之一执行切割操作,以得到两块更小的矩形木块:
- 沿垂直方向按高度 完全 切割木块,或
- 沿水平方向按宽度 完全 切割木块
在将一块木块切成若干小木块后,你可以根据 prices 卖木块。你可以卖多块同样尺寸的木块。你不需要将所有小木块都卖出去。你 不能
旋转切好后木块的高和宽。
请你返回切割一块大小为 _ _m x n __ 的木块后,能得到的 最多 钱数。
注意你可以切割木块任意次。
示例 1:
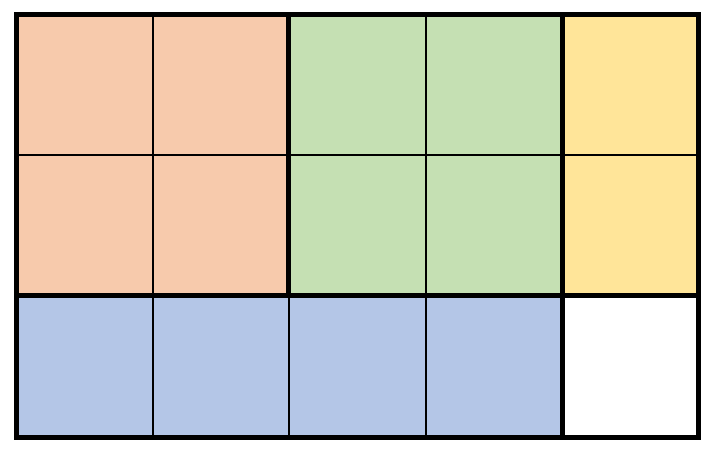
**输入:** m = 3, n = 5, prices = [[1,4,2],[2,2,7],[2,1,3]]
**输出:** 19
**解释:** 上图展示了一个可行的方案。包括:
- 2 块 2 x 2 的小木块,售出 2 * 7 = 14 元。
- 1 块 2 x 1 的小木块,售出 1 * 3 = 3 元。
- 1 块 1 x 4 的小木块,售出 1 * 2 = 2 元。
总共售出 14 + 3 + 2 = 19 元。
19 元是最多能得到的钱数。
示例 2:
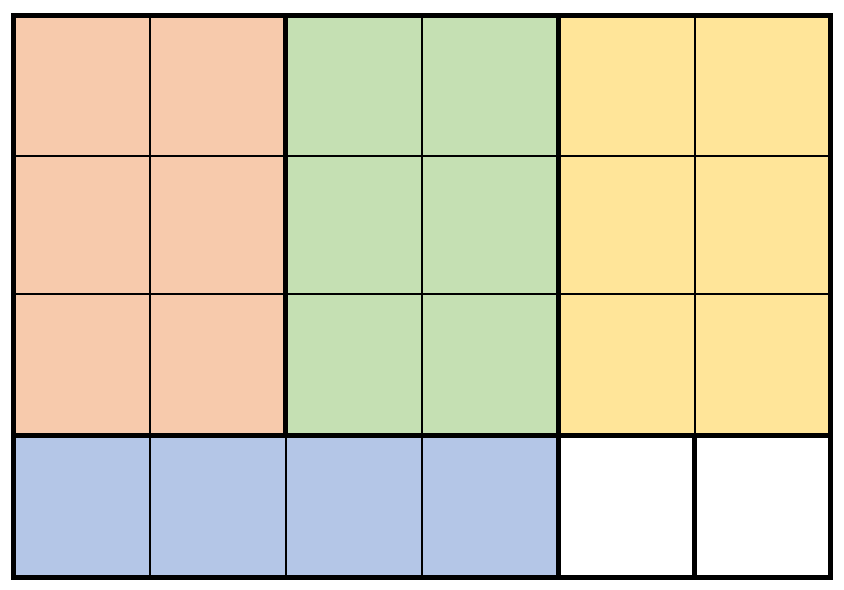
**输入:** m = 4, n = 6, prices = [[3,2,10],[1,4,2],[4,1,3]]
**输出:** 32
**解释:** 上图展示了一个可行的方案。包括:
- 3 块 3 x 2 的小木块,售出 3 * 10 = 30 元。
- 1 块 1 x 4 的小木块,售出 1 * 2 = 2 元。
总共售出 30 + 2 = 32 元。
32 元是最多能得到的钱数。
注意我们不能旋转 1 x 4 的木块来得到 4 x 1 的木块。
提示:
1 <= m, n <= 2001 <= prices.length <= 2 * 104prices[i].length == 31 <= hi <= m1 <= wi <= n1 <= pricei <= 106- 所有
(hi, wi)互不相同 。
方法一:动态规划 / 记忆化搜索
思路与算法
我们可以使用动态规划来解决本题。
我们用 f(x, y) 表示当木块的高和宽分别是 x 和 y 时,可以得到的最多钱数。我们需要考虑三种情况:
- 如果数组 prices 中存在 (x, y, \textit{price}) 这一三元组,那么我们可以将木块以 prices 的价格卖出。为了快速判断存在性,我们可以使用一个哈希映射来进行存储,即哈希映射的键为 (h_i, w_i),值为 price}_i,这样我们就可以根据木块的高和宽,在 O(1) 的时间得到对应的价格。这种情况的状态转移方程为:
f(x, y) = \textit{price}
- 如果 x>1,那么我们可以沿水平方向将木块切成两部分,它们的高分别是 i~(1 \leq i < x) 和 x-i,宽均为 y。因此我们可以得到状态转移方程:
f(x, y) = \max_{1 \leq i < x} \big{ f(i, y) + f(x-i, y) \big}
- 如果 y>1,那么我们可以沿垂直方向将木块切成两部分,它们的宽分别是 j~(1 \leq j < y) 和 y-j,高均为 x。因此我们可以得到状态转移方程:
f(x, y) = \max_{1 \leq j < y} \big{ f(x, j) + f(x, y-j) \big}
当有多种情况满足时,我们需要选择它们中的较大值。最终的答案即为 f(m, n)。
细节
本题使用记忆化搜索进行编码更加简洁方便。
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(mn(m+n)+p),其中 p 是数组 prices 的长度。
空间复杂度:O(mn+p),即为哈希映射和动态规划的数组需要使用的空间。
Comments