2320-统计放置房子的方式数

一条街道上共有 n * 2 个 地块 ，街道的两侧各有 n 个地块。每一边的地块都按从 1 到 n
编号。每个地块上都可以放置一所房子。

现要求街道同一侧不能存在两所房子相邻的情况，请你计算并返回放置房屋的方式数目。由于答案可能很大，需要对 109 + 7 取余后再返回。

注意，如果一所房子放置在这条街某一侧上的第 i 个地块，不影响在另一侧的第 i 个地块放置房子。

示例 1：

**输入：** n = 1
**输出：** 4
**解释：**
可能的放置方式：
1. 所有地块都不放置房子。
2. 一所房子放在街道的某一侧。
3. 一所房子放在街道的另一侧。
4. 放置两所房子，街道两侧各放置一所。

示例 2：

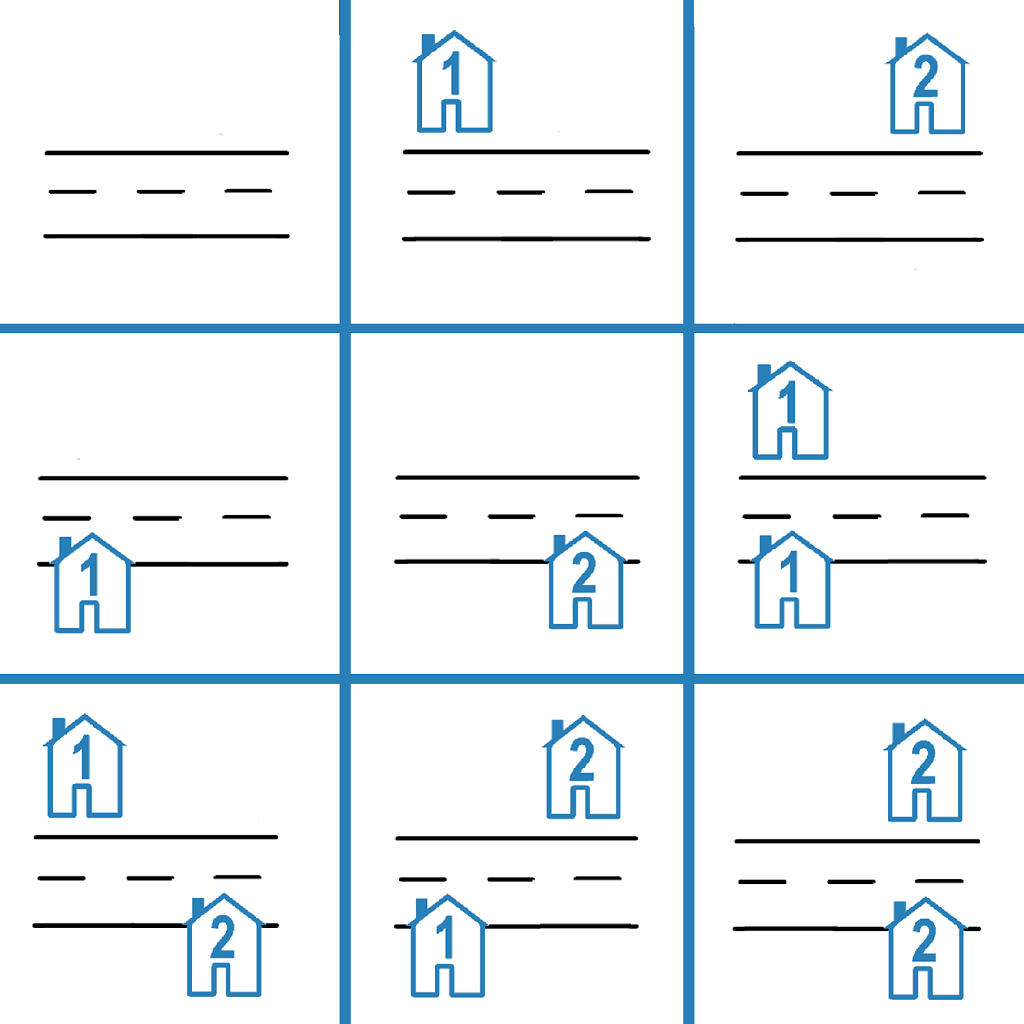
**输入：** n = 2
**输出：** 9
**解释：** 如上图所示，共有 9 种可能的放置方式。

提示：

• 1 <= n <= 104

本题 视频讲解 已出炉，欢迎点赞三连~

---

单独考虑一侧的房子，定义 f[i] 表示前 i 个地块的放置方案数，其中第 i 个地块可以放房子，也可以不放房子。

考虑第 i 个地块：

• 若不放房子，那么第 i-1 个地块可放可不放，则有 f[i] = f[i-1]；
• 若放房子，那么第 i-1 个地块无法放房子，第 i-2 个地块可放可不放，则有 f[i] = f[i-2]。

因此

f[i] = f[i-1] + f[i-2]

边界为

• f[0]=1，空也是一种方案；
• f[1]=2，放与不放两种方案。

由于两侧的房屋互相独立，根据乘法原理，答案为 f[n]^2。

[sol1-Python3]

MOD = 10 ** 9 + 7
f = [1, 2]
for _ in range(10 ** 4 - 1):
    f.append((f[-1] + f[-2]) % MOD)

class Solution:
    def countHousePlacements(self, n: int) -> int:
        return f[n] ** 2 % MOD

[sol1-Java]

class Solution {
    static final int MOD = (int) 1e9 + 7, MX = (int) 1e4 + 1;
    static final int[] f = new int[MX];

    static {
        f[0] = 1;
        f[1] = 2;
        for (var i = 2; i < MX; ++i)
            f[i] = (f[i - 1] + f[i - 2]) % MOD;
    }

    public int countHousePlacements(int n) {
        return (int) ((long) f[n] * f[n] % MOD);
    }
}

[sol1-C++]

const int MOD = 1e9 + 7, MX = 1e4 + 1;
int f[MX] = {1, 2};
int init = []() {
    for (int i = 2; i < MX; ++i)
        f[i] = (f[i - 1] + f[i - 2]) % MOD;
    return 0;
}();

class Solution {
public:
    int countHousePlacements(int n) {
        return (long) f[n] * f[n] % MOD;
    }
};

[sol1-Go]

const mod int = 1e9 + 7
var f = [1e4 + 1]int{1, 2}
func init() {
	for i := 2; i <= 1e4; i++ {
		f[i] = (f[i-1] + f[i-2]) % mod
	}
}

func countHousePlacements(n int) int {
	return f[n] * f[n] % mod
}