给你一棵 完整二叉树 的根,这棵树有以下特征:
- 叶子节点 要么值为
0 要么值为 1 ,其中 0 表示 False ,1 表示 True 。
- 非叶子节点 要么值为
2 要么值为 3 ,其中 2 表示逻辑或 OR ,3 表示逻辑与 AND 。
计算 一个节点的值方式如下:
- 如果节点是个叶子节点,那么节点的 值 为它本身,即
True 或者 False 。
- 否则, 计算 两个孩子的节点值,然后将该节点的运算符对两个孩子值进行 运算 。
返回根节点 _ _root 的布尔运算值。
完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。
叶子节点 是没有孩子的节点。
示例 1:

**输入:** root = [2,1,3,null,null,0,1]
**输出:** true
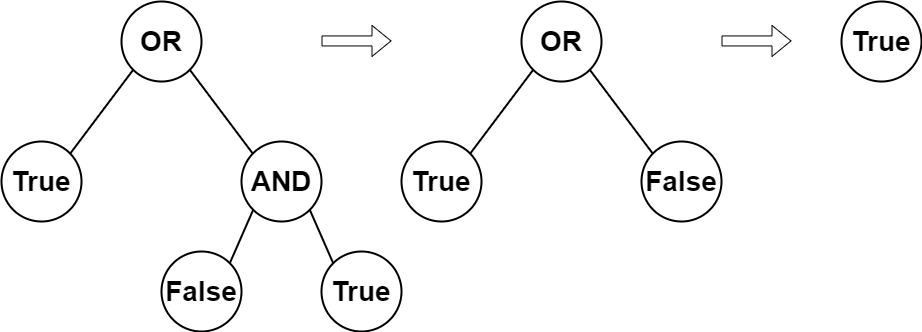
**解释:** 上图展示了计算过程。
AND 与运算节点的值为 False AND True = False 。
OR 运算节点的值为 True OR False = True 。
根节点的值为 True ,所以我们返回 true 。
示例 2:
**输入:** root = [0]
**输出:** false
**解释:** 根节点是叶子节点,且值为 false,所以我们返回 false 。
提示:
- 树中节点数目在
[1, 1000] 之间。
0 <= Node.val <= 3- 每个节点的孩子数为
0 或 2 。
- 叶子节点的值为
0 或 1 。
- 非叶子节点的值为
2 或 3 。
方法一:递归
思路与算法
根据题目要求,如果当前节点为叶子节点,那么节点的值为它本身;否则节点的值为两个孩子的节点值的逻辑运算结果。我们可以使用递归,如果要计算出当前节点 node 的值,我们需要先计算出两个叶子节点组成的子树的值分别为 lval 与 lval,然后再计算出当前节点组成的子树的值。计算过程如下:
- 如果当前节点 node 为叶子节点,则直接返回当前节点的值。根据题中完整二叉树的定义,树中每个节点有 0 个或者 2 个孩子的二叉树,只需检测该节点是否有左孩子或者右孩子即可。
- 如果当前节点 node 含有孩子节点,计算出其左右孩子节点的值为 lval 与 rval。如果 node 节点的值为 2,则返回 lval}
| \textit{rval;如果 node 节点的值为 3,则返回 lval} & \textit{rval。
代码
[sol1-Python3]1
2
3
4
5
6
7
| class Solution:
def evaluateTree(self, root: Optional[TreeNode]) -> bool:
if root.left is None:
return root.val == 1
if root.val == 2:
return self.evaluateTree(root.left) or self.evaluateTree(root.right)
return self.evaluateTree(root.left) and self.evaluateTree(root.right)
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public:
bool evaluateTree(TreeNode* root) {
if (root->left == nullptr) {
return root->val;
}
if (root->val == 2) {
return evaluateTree(root->left) || evaluateTree(root->right);
} else {
return evaluateTree(root->left) && evaluateTree(root->right);
}
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
| class Solution {
public boolean evaluateTree(TreeNode root) {
if (root.left == null) {
return root.val == 1;
}
if (root.val == 2) {
return evaluateTree(root.left) || evaluateTree(root.right);
} else {
return evaluateTree(root.left) && evaluateTree(root.right);
}
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
| public class Solution {
public bool EvaluateTree(TreeNode root) {
if (root.left == null) {
return root.val == 1;
}
if (root.val == 2) {
return EvaluateTree(root.left) || EvaluateTree(root.right);
} else {
return EvaluateTree(root.left) && EvaluateTree(root.right);
}
}
}
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
| bool evaluateTree(struct TreeNode* root) {
if (!root->left) {
return root->val;
}
if (root->val == 2) {
return evaluateTree(root->left) || evaluateTree(root->right);
} else {
return evaluateTree(root->left) && evaluateTree(root->right);
}
}
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
| var evaluateTree = function(root) {
if (!root.left) {
return root.val === 1;
}
if (root.val === 2) {
return evaluateTree(root.left) || evaluateTree(root.right);
} else {
return evaluateTree(root.left) && evaluateTree(root.right);
}
};
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
| func evaluateTree(root *TreeNode) bool {
if root.Left == nil {
return root.Val == 1
}
if root.Val == 2 {
return evaluateTree(root.Left) || evaluateTree(root.Right)
}
return evaluateTree(root.Left) && evaluateTree(root.Right)
}
|
复杂度分析