2368-受限条件下可到达节点的数目
现有一棵由 n 个节点组成的无向树,节点编号从 0 到 n - 1 ,共有 n - 1 条边。
给你一个二维整数数组 edges ,长度为 n - 1 ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi
之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。
在不访问受限节点的前提下,返回你可以从节点 __0 __ 到达的 最多 节点数目 。
注意,节点 0 不 会标记为受限节点。
示例 1:
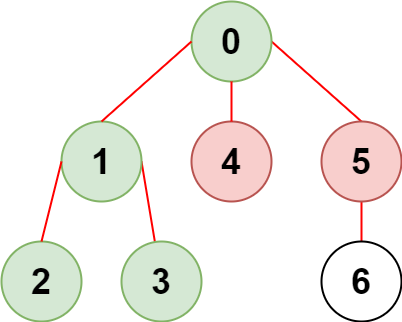
**输入:** n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
**输出:** 4
**解释:** 上图所示正是这棵树。
在不访问受限节点的前提下,只有节点 [0,1,2,3] 可以从节点 0 到达。
示例 2:
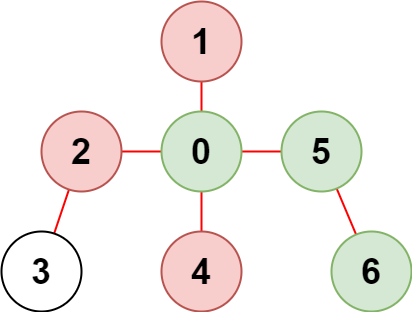
**输入:** n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
**输出:** 3
**解释:** 上图所示正是这棵树。
在不访问受限节点的前提下,只有节点 [0,5,6] 可以从节点 0 到达。
提示:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges表示一棵有效的树1 <= restricted.length < n1 <= restricted[i] < nrestricted中的所有值 互不相同
视频讲解 已出炉,欢迎点赞三连,在评论区分享你对这场周赛的看法~
用哈希表记录哪些节点是受限的,建图的时候只有当两个节点都不是受限的才连边。然后 DFS 这棵树,统计从 0 出发能访问到的节点数,即为答案。
1 | class Solution: |
1 | func reachableNodes(n int, edges [][]int, restricted []int) (ans int) { |
Comments