给你一个小写英文字母组成的字符串 s 和一个二维整数数组 shifts ，其中 shifts[i] = [starti, endi, directioni] 。对于每个 i ，将 s 中从下标 starti 到下标 endi （两者都包含）所有字符都进行移位运算，如果
directioni = 1 将字符向后移位，如果 directioni = 0 将字符向前移位。

将一个字符向后移位的意思是将这个字符用字母表中 下一个 字母替换（字母表视为环绕的，所以 'z' 变成
'a'）。类似的，将一个字符向前移位的意思是将这个字符用字母表中 前一个 字母替换（字母表是环绕的，所以 'a' 变成
'z' ）。

请你返回对 s 进行所有移位操作以后得到的最终字符串。

示例 1：

**输入：** s = "abc", shifts = [[0,1,0],[1,2,1],[0,2,1]]
**输出：** "ace"
**解释：** 首先，将下标从 0 到 1 的字母向前移位，得到 s = "zac" 。
然后，将下标从 1 到 2 的字母向后移位，得到 s = "zbd" 。
最后，将下标从 0 到 2 的字符向后移位，得到 s = "ace" 。

示例 2:

**输入：** s = "dztz", shifts = [[0,0,0],[1,1,1]]
**输出：** "catz"
**解释：** 首先，将下标从 0 到 0 的字母向前移位，得到 s = "cztz" 。
最后，将下标从 1 到 1 的字符向后移位，得到 s = "catz" 。

提示：

1 <= s.length, shifts.length <= 5 * 104
shifts[i].length == 3
0 <= starti <= endi < s.length
0 <= directioni <= 1
s 只包含小写英文字母。

如果想要查看作者更多文章，可以点击此处！！！🔥🔥🔥

为了本篇文章更好的观感，可以点击此处！！！

6158. 字母移位 II

1109. 航班预订统计

1094. 拼车

在介绍差分数组之前，先回顾一下「前缀和数组」详情可见前缀和数组

前缀和主要适用的场景是原始数组不会被修改的情况下，频繁查询某个区间的累加和

差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减

使用场景：对于一个数组 nums[]

要求一：对 num[2...4] 全部 + 1
要求二：对 num[1...3] 全部 - 3
要求三：对 num[0...4] 全部 + 9

看到上述情景，首先想到的肯定是遍历（bao li）。直接对数组循环 3 遍，每次在规定的区间上按要求进行操作，此时时间复杂度 O(3n)

但是当这样的操作变得频繁后，时间复杂度也呈线性递增

所以针对这种场景，提出了「差分数组」的概念，举个简单的例子

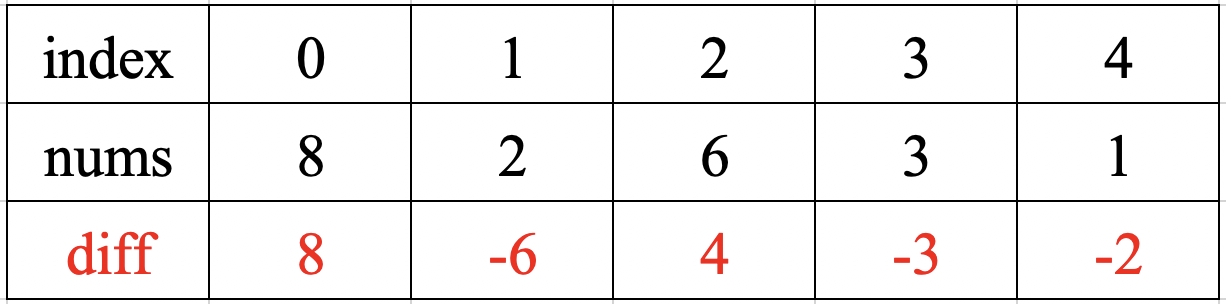
diff[] 和 nums[] 的关系：diff[i] = nums[i] - nums[i - 1]，diff[0] 除外

问题一：这样处理的好处是什么呢？？？？？

当我们需要对 nums[] 进行上述三个要求时，不需要一次一次的遍历整个数组了，而只需要对 diff[] 进行一次 O(1) 的操作即可

要求一：diff[2] += 1;
要求二：diff[1] += (-3); diff[3 + 1] -= (-3);
要求三：diff[0] += 9;

总结：对于改变区间 [i, j] 的值，只需要进行如下操作 diff[i] += val; diff[j + 1] -= val

注：当 j + 1 >= diff.length 时，不需要进行 diff[j + 1] -= val 操作

问题二：怎么通过 diff[] 得到更新后的数组呢？？？？？

// 复原操作
int[] res = new int[n];
// 下标为 0 的元素相等
res[0] = diff[0];
for (int i = 1; i < n; i++) {
    res[i] = diff[i] + res[i - 1];
}

问题三：diff[] 原理

当我们需要对区间 [i, j] 进行 + val 操作时，我们对 diff[i] += val; diff[j + 1] -= val;

在复原操作时，当我们求 res[i] 时，res[i - 1] 没有变，而 diff[i] 增加了 3，所以 res[i] 增加 3

当我们求 res[i + 1] 时，res[i] 增加了 3，而 diff[i + 1] 没有变，故 res[i + 1] = diff[i + 1] + res[i] 增加 3。即：虽然 diff[i + 1] 没有变，但是 res[i] 对后面的 res[i + 1] 有一个累积作用

当我们求 res[j + 1] 时，res[j] 增加了 3，而 diff[j + 1] 减少了 3，故 res[j + 1] = diff[j + 1] + res[j] 增加没有变。即：我们在 j + 1 的时候，把上述的累积作用去除了，所以 j + 1 后面的元素不受影响

完整模版

public class Difference {

    /**
     * 差分数组
     */
    private final int[] diff;

    /**
     * 初始化差分数组
     * @param nums nums
     */
    public Difference(int[] nums) {
        assert nums.length > 0;
        diff = new int[nums.length];
        diff[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            diff[i] = nums[i] - nums[i - 1];
        }
    }

    /**
     * 对区间 [i, j] 增加 val（val 可为负数）
     * @param i i
     * @param j j
     * @param val val
     */
    public void increment(int i, int j, int val) {
        diff[i] += val;
        if (j + 1 < diff.length) {
            diff[j + 1] -= val;
        }
    }

    /**
     * 复原操作
     * @return res
     */
    public int[] result() {
        int[] res = new int[diff.length];
        res[0] = diff[0];
        for (int i = 1; i < diff.length; i++) {
            res[i] = res[i - 1] + diff[i];
        }
        return res;
    }
}

字母移位 II

题目详情可见字母移位 II

public String shiftingLetters(String s, int[][] shifts) {
    Difference diff = new Difference(new int[s.length()]);
    for (int[] shift : shifts) {
        diff.increment(shift[0], shift[1], shift[2] == 1 ? 1 : -1);
    }
    int[] res = diff.result();
    char[] cur = s.toCharArray();
    for (int i = 0; i < s.length(); i++) {
        int c = cur[i] - 'a';
        c = ((c + res[i]) % 26 + 26) % 26;
        cur[i] = (char) (c + 'a');
    }
    return new String(cur);
}

2381-字母移位 II

如果想要查看作者更多文章，可以点击此处！！！🔥🔥🔥

为了本篇文章更好的观感，可以点击此处！！！

字母移位 II