2385-感染二叉树需要的总时间
给你一棵二叉树的根节点 root ,二叉树中节点的值 互不相同 。另给你一个整数 start 。在第 0 分钟, 感染
将会从值为 start 的节点开始爆发。
每分钟,如果节点满足以下全部条件,就会被感染:
- 节点此前还没有感染。
- 节点与一个已感染节点相邻。
返回感染整棵树需要的分钟数 。
示例 1:
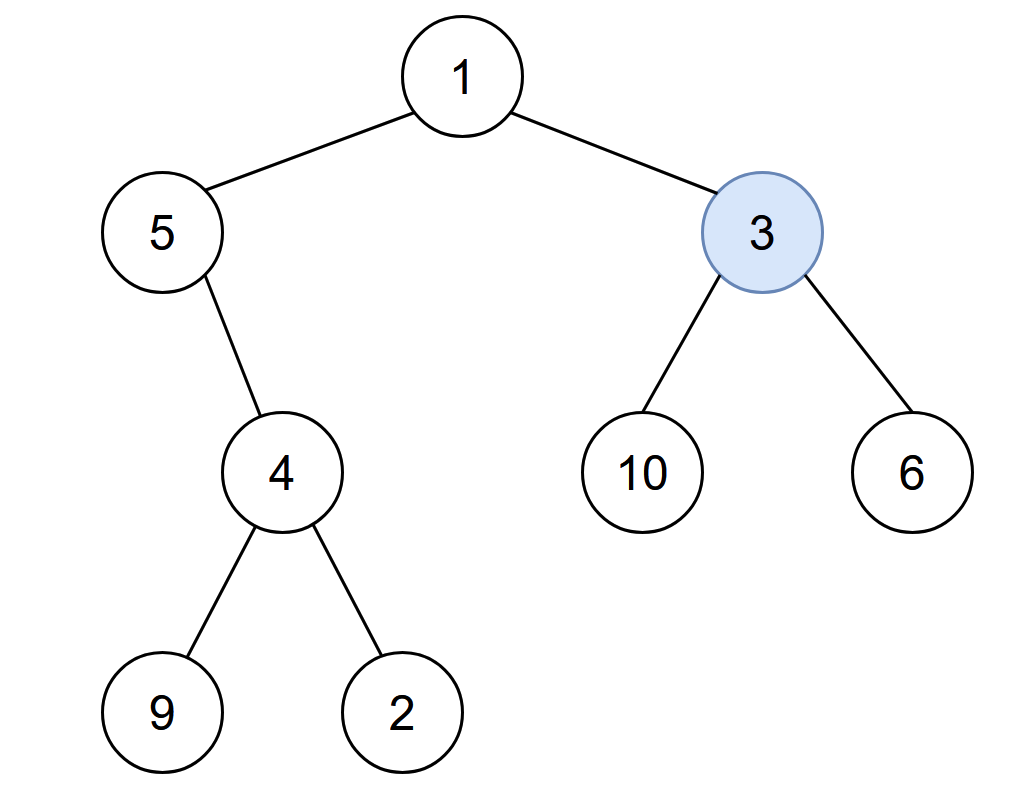
**输入:** root = [1,5,3,null,4,10,6,9,2], start = 3
**输出:** 4
**解释:** 节点按以下过程被感染:
- 第 0 分钟:节点 3
- 第 1 分钟:节点 1、10、6
- 第 2 分钟:节点5
- 第 3 分钟:节点 4
- 第 4 分钟:节点 9 和 2
感染整棵树需要 4 分钟,所以返回 4 。
示例 2:

**输入:** root = [1], start = 1
**输出:** 0
**解释:** 第 0 分钟,树中唯一一个节点处于感染状态,返回 0 。
提示:
- 树中节点的数目在范围
[1, 105]内 1 <= Node.val <= 105- 每个节点的值 互不相同
- 树中必定存在值为
start的节点
解题思路

- 对于起始结点,若该结点是一棵树的根结点,那么该结点感染整棵树所需时间为树的高度。如图中的
3->10,6。 - 若起始节点存在父结点,则该结点还可以沿着父结点去感染父结点其其他子树。如图中的
3->1->5->4->9,2。假设该起始结点在某结点的左子树上,那么它感染整棵树的时间为从起始节点到树的根结点的距离 + 根结点另一颗子树的高度。即根结点与起始节点的高度差 + 根结点另一颗子树的高度。 - 以上两种情况是同时进行的,所以最短时间为两者的最大值。
代码
1 | class Solution { |
Comments