2471-逐层排序二叉树所需的最少操作数目

给你一个 值互不相同 的二叉树的根节点 root 。

在一步操作中，你可以选择 同一层 上任意两个节点，交换这两个节点的值。

返回每一层按 严格递增顺序 排序所需的最少操作数目。

节点的 层数 是该节点和根节点之间的路径的边数。

示例 1 ：

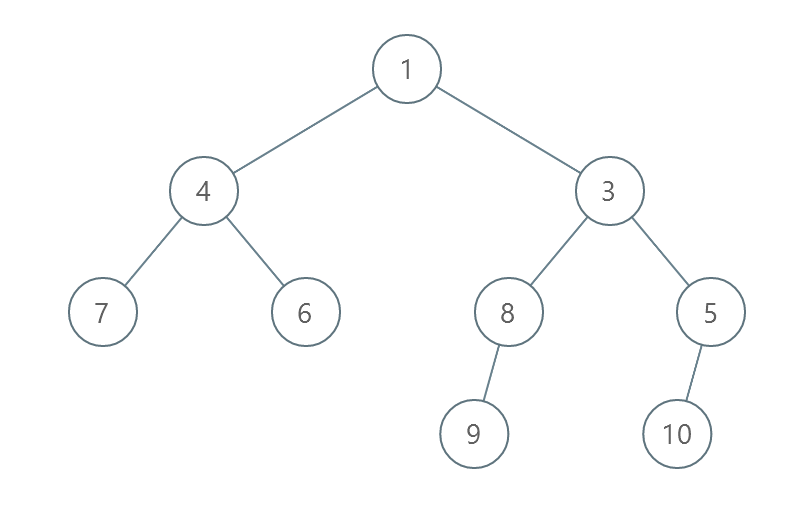
**输入：** root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
**输出：** 3
**解释：**
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
共计用了 3 步操作，所以返回 3 。
可以证明 3 是需要的最少操作数目。

示例 2 ：

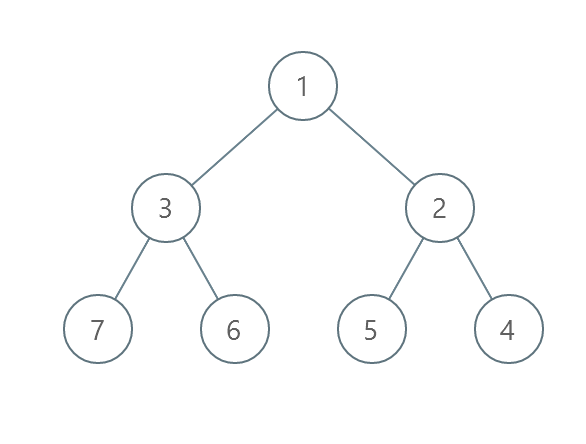
**输入：** root = [1,3,2,7,6,5,4]
**输出：** 3
**解释：** - 交换 3 和 2 。第 2 层变为 [2,3] 。 
- 交换 7 和 4 。第 3 层变为 [4,6,5,7] 。 
- 交换 6 和 5 。第 3 层变为 [4,5,6,7] 。
共计用了 3 步操作，所以返回 3 。 
可以证明 3 是需要的最少操作数目。

示例 3 ：

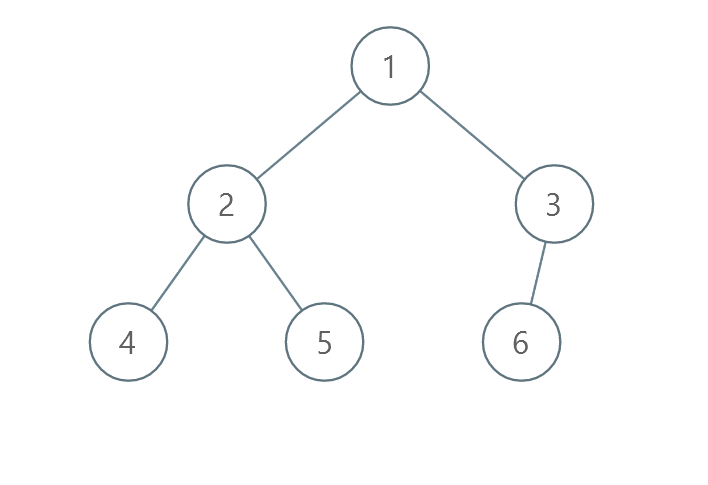
**输入：** root = [1,2,3,4,5,6]
**输出：** 0
**解释：** 每一层已经按递增顺序排序，所以返回 0 。

提示：

• 树中节点的数目在范围 [1, 105] 。
• 1 <= Node.val <= 105
• 树中的所有值 互不相同 。

视频讲解 已出炉，欢迎点赞三连，在评论区分享你对这场周赛的看法~

---

这是一个经典问题，做法是置换环。

例如在数组 [2,0,1,4,3] 中，[2,0,1] 和 [4,3] 分别是两个置换环，环与环之间是数字是不需要发生交换的，只会在环内发生交换。

怎么找到环呢？从第一个数开始，把这个数字当成下标去访问数组，不断循环直到回到这个数本身。

我们只需要计算每个环内需要多少次交换。对于每个环，交换次数为环的大小减一。

代码实现时需要离散化。

[sol1-Python3]

class Solution:
    def minimumOperations(self, root: Optional[TreeNode]) -> int:
        ans, q = 0, [root]
        while q:
            a = []
            tmp = q
            q = []
            for node in tmp:
                a.append(node.val)
                if node.left: q.append(node.left)
                if node.right: q.append(node.right)

            n = len(a)
            a = sorted(range(n), key=lambda i: a[i])  # 离散化

            ans += n
            vis = [False] * n
            for v in a:
                if vis[v]: continue
                while not vis[v]:
                    vis[v] = True
                    v = a[v]
                ans -= 1
        return ans

[sol1-Go]

func minimumOperations(root *TreeNode) (ans int) {
	q := []*TreeNode{root}
	for len(q) > 0 {
		n := len(q)
		a := make([]int, n)
		tmp := q
		q = nil
		for i, node := range tmp {
			a[i] = node.Val
			if node.Left != nil {
				q = append(q, node.Left)
			}
			if node.Right != nil {
				q = append(q, node.Right)
			}
		}

		id := make([]int, n) // 离散化后的数组
		for i := range id {
			id[i] = i
		}
		sort.Slice(id, func(i, j int) bool { return a[id[i]] < a[id[j]] })

		ans += n
		vis := make([]bool, n)
		for _, v := range id {
			if !vis[v] {
				for ; !vis[v]; v = id[v] {
					vis[v] = true
				}
				ans--
			}
		}
	}
	return
}

复杂度分析

• 时间复杂度：O(n\log n)，其中 n 为二叉树的节点个数。瓶颈在排序上，对于完全二叉树而言，最后一层的节点个数可以达到 O(n)。
• 空间复杂度：O(n)。

相似题目

• 765. 情侣牵手