2476-二叉搜索树最近节点查询

给你一个 二叉搜索树 的根节点 root ，和一个由正整数组成、长度为 n 的数组 queries 。

请你找出一个长度为 n 的 二维 答案数组 answer ，其中 answer[i] = [mini, maxi] ：

• mini 是树中小于等于 queries[i] 的 最大值 。如果不存在这样的值，则使用 -1 代替。
• maxi 是树中大于等于 queries[i] 的 最小值 。如果不存在这样的值，则使用 -1 代替。

返回数组 answer 。

示例 1 ：

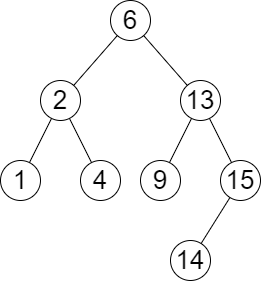
**输入：** root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16]
**输出：** [[2,2],[4,6],[15,-1]]
**解释：** 按下面的描述找出并返回查询的答案：
- 树中小于等于 2 的最大值是 2 ，且大于等于 2 的最小值也是 2 。所以第一个查询的答案是 [2,2] 。
- 树中小于等于 5 的最大值是 4 ，且大于等于 5 的最小值是 6 。所以第二个查询的答案是 [4,6] 。
- 树中小于等于 16 的最大值是 15 ，且大于等于 16 的最小值不存在。所以第三个查询的答案是 [15,-1] 。

示例 2 ：

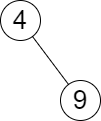
**输入：** root = [4,null,9], queries = [3]
**输出：** [[-1,4]]
**解释：** 树中不存在小于等于 3 的最大值，且大于等于 3 的最小值是 4 。所以查询的答案是 [-1,4] 。

提示：

• 树中节点的数目在范围 [2, 105] 内
• 1 <= Node.val <= 106
• n == queries.length
• 1 <= n <= 105
• 1 <= queries[i] <= 106

视频讲解 已出炉，欢迎点赞三连，在评论区分享你对这场周赛的看法~

---

首先，题目没说二叉搜索树是平衡的，最坏情况下二叉搜索树是一条链。

因此需要通过一次 94. 二叉树的中序遍历 得到有一个有序数组，再在数组上做二分查找。

在有序数组中求大于等于和小于等于，和 34. 在排序数组中查找元素的第一个和最后一个位置 是一样的。

我在 二分查找又死循环了？一个视频讲透二分本质！【基础算法精讲 04】 这期视频中详细讲解了二分查找，欢迎观看。

[sol1-Python3]

class Solution:
    def closestNodes(self, root: Optional[TreeNode], queries: List[int]) -> List[List[int]]:
        a = []
        def dfs(o: Optional[TreeNode]) -> None:
            if o is None: return
            dfs(o.left)
            a.append(o.val)
            dfs(o.right)
        dfs(root)

        ans = []
        for q in queries:
            j = bisect_right(a, q)
            min = a[j - 1] if j else -1
            j = bisect_left(a, q)
            max = a[j] if j < len(a) else -1
            ans.append([min, max])
        return ans

[sol1-Go]

func closestNodes(root *TreeNode, queries []int) [][]int {
	a := []int{}
	var dfs func(*TreeNode)
	dfs = func(o *TreeNode) {
		if o == nil {
			return
		}
		dfs(o.Left)
		a = append(a, o.Val)
		dfs(o.Right)
	}
	dfs(root)

	ans := make([][]int, len(queries))
	for i, q := range queries {
		min, max := -1, -1
		// 这是怎么转换的，可以看我上面贴的视频链接
		j := sort.SearchInts(a, q+1) - 1
		if j >= 0 {
			min = a[j]
		}
		j = sort.SearchInts(a, q)
		if j < len(a) {
			max = a[j]
		}
		ans[i] = []int{min, max}
	}
	return ans
}

复杂度分析

• 时间复杂度：O(n + q\log n)，其中 q 为 queries 的长度，n 为二叉搜索树的节点个数。
• 空间复杂度：O(n)。