2498-青蛙过河 II

给你一个下标从 0 开始的整数数组 stones ，数组中的元素 严格递增 ，表示一条河中石头的位置。

一只青蛙一开始在第一块石头上，它想到达最后一块石头，然后回到第一块石头。同时每块石头 至多 到达 一次。

一次跳跃的 长度 是青蛙跳跃前和跳跃后所在两块石头之间的距离。

• 更正式的，如果青蛙从 stones[i] 跳到 stones[j] ，跳跃的长度为 |stones[i] - stones[j]| 。

一条路径的 代价 是这条路径里的 最大跳跃长度 。

请你返回这只青蛙的 最小代价 。

示例 1：

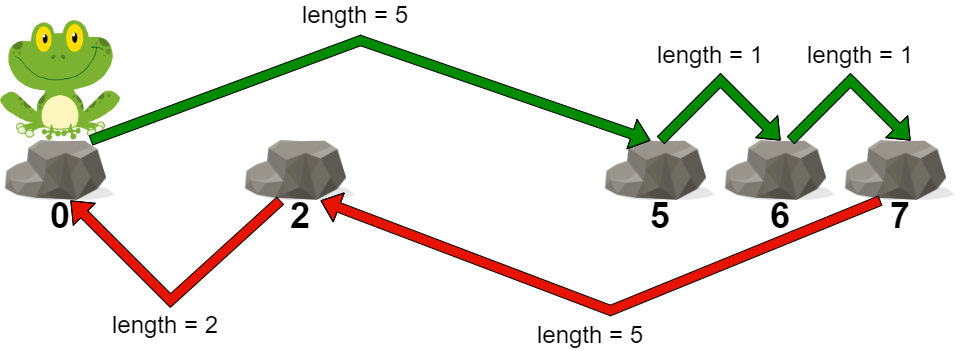
**输入：** stones = [0,2,5,6,7]
**输出：** 5
**解释：** 上图展示了一条最优路径。
这条路径的代价是 5 ，是这条路径中的最大跳跃长度。
无法得到一条代价小于 5 的路径，我们返回 5 。

示例 2：

**输入：** stones = [0,3,9]
**输出：** 9
**解释：**
青蛙可以直接跳到最后一块石头，然后跳回第一块石头。
在这条路径中，每次跳跃长度都是 9 。所以路径代价是 max(9, 9) = 9 。
这是可行路径中的最小代价。

提示：

• 2 <= stones.length <= 105
• 0 <= stones[i] <= 109
• stones[0] == 0
• stones 中的元素严格递增。

视频讲解 已出炉，欢迎点赞三连，在评论区分享你对这场双周赛的看法~

---

首先每个石头都需要选，这样可以尽量让最大距离最小。

如何跳呢？比如四块石头 a-b-c-d：

• 不采用间隔跳，路径为 a-d-c-b-a；
• 采用间隔跳，路径为 a-c-d-b-a；

由于 a-d 必然比 a-c 和 b-d 大，从这点可以看出，间隔跳是最优的。

该结论可以推广至更多的石头的情况。

[sol1-Python3]

class Solution:
    def maxJump(self, stones: List[int]) -> int:
        ans = stones[1] - stones[0]
        for i in range(2, len(stones)):
            ans = max(ans, stones[i] - stones[i - 2])
        return ans

[sol1-Go]

func maxJump(stones []int) int {
	ans := stones[1] - stones[0]
	for i := 2; i < len(stones); i++ {
		ans = max(ans, stones[i]-stones[i-2])
	}
	return ans
}

func max(a, b int) int { if b > a { return b }; return a }

复杂度分析

• 时间复杂度：O(n)，其中 n 为 stones 的长度。
• 空间复杂度：O(1)，仅用到若干额外变量。