给你一个大小为 m x n 的整数矩阵 grid 和一个大小为 k 的数组 queries 。
找出一个大小为 k 的数组 answer ,且满足对于每个整数 queries[i] ,你从矩阵 左上角 单元格开始,重复以下过程:
- 如果
queries[i] 严格 大于你当前所处位置单元格,如果该单元格是第一次访问,则获得 1 分,并且你可以移动到所有 4 个方向(上、下、左、右)上任一 相邻 单元格。
- 否则,你不能获得任何分,并且结束这一过程。
在过程结束后,answer[i] 是你可以获得的最大分数。注意,对于每个查询,你可以访问同一个单元格 多次 。
返回结果数组 answer 。
示例 1:

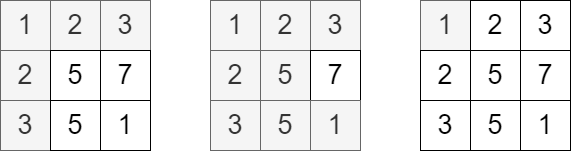
**输入:** grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2]
**输出:** [5,8,1]
**解释:** 上图展示了每个查询中访问并获得分数的单元格。
示例 2:

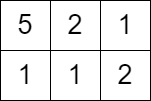
**输入:** grid = [[5,2,1],[1,1,2]], queries = [3]
**输出:** [0]
**解释:** 无法获得分数,因为左上角单元格的值大于等于 3 。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 105k == queries.length1 <= k <= 1041 <= grid[i][j], queries[i] <= 106
前言
根据查询规则,如果一次查询的值是 q,则查询结果为从矩阵左上角单元格开始可以移动到的值小于 q 的单元格的数目。
朴素的做法是对于每个查询分别遍历矩阵 grid 计算可以获得的最大分数。由于矩阵的大小是 m \times n,因此朴素的做法对于每次查询需要 O(mn) 的时间,查询次数是 k,则时间复杂度是 O(mnk),该时间复杂度过高,需要优化。
如果两次查询的值分别是 q_1 和 q_2,其中 q_1 \le q_2,则 q_1 对应可以移动到的所有单元格都是 q_2 对应可以移动到的单元格,即 q_2 的查询结果中的单元格包含 q_1 的查询结果中的所有单元格。因此可以按照查询值递增的顺序依次计算每个查询的结果,对于每个查询只需要考虑新增加的可以移动到的单元格的数目,达到优化时间复杂度的目的。
为了优化时间复杂度,需要将查询数组 queries 按查询值递增顺序排序,然后遍历排序后的查询数组,计算每个查询的结果。由于结果数组需要按照原始查询数组的顺序返回,因此将查询数组排序时需要维护原始下标信息,为了实现这一点,需要新建一个数组存储每个查询的值和下标,然后将新数组按查询值递增顺序排序。遍历排序后的新数组时,对于每个查询,可以得到该查询在原始查询数组中的下标,将查询结果填到相应下标处。
有两种优化时间复杂度的做法,分别是基于优先队列的广度优先搜索和并查集。
解法一
思路和算法
使用基于优先队列的广度优先搜索实现时,需要使用与矩阵相同大小的二维数组记录每个单元格是否被访问过,使用优先队列存储已访问的单元格的行列下标和单元格的值,优先队列的队首元素是值最小的单元格。一个单元格的状态是已访问表示在已经遍历的查询中该单元格可以到达,但是不一定包含在查询结果中,只有当一个可以到达的单元格的值小于查询值时才包含在查询结果中。初始时,只有左上角单元格的状态是已访问,优先队列只包含左上角单元格,其余单元格的状态都是未访问。
按查询值递增顺序遍历每个查询,遍历过程中维护查询的分数,则遍历过程中的查询的分数总是递增的。初始时查询的分数是 0。
对于每个查询,执行如下操作。
当优先队列不为空且优先队列的队首单元格的值小于查询值时,优先队列的队首单元格为可以移动到的值小于查询值的单元格,因此将查询的分数加 1,将队首单元格取出,将该单元格的所有相邻且未访问的单元格加入优先队列。重复该操作直到优先队列为空或优先队列的队首单元格的值大于等于查询值。
将查询的分数作为当前查询的结果,填到结果数组的相应下标处。
遍历所有的查询之后,即可得到结果数组。
代码
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
static int[][] dirs = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };
public int[] maxPoints(int[][] grid, int[] queries) {
int k = queries.length;
int[][] queriesIndices = new int[k][2];
for (int i = 0; i < k; i++) {
queriesIndices[i][0] = queries[i];
queriesIndices[i][1] = i;
}
Arrays.sort(queriesIndices, (a, b) -> a[0] - b[0]);
int[] answer = new int[k];
int points = 0;
int m = grid.length, n = grid[0].length;
boolean[][] visited = new boolean[m][n];
visited[0][0] = true;
PriorityQueue<int[]> pq = new PriorityQueue<int[]>((a, b) -> a[2] - b[2]);
pq.offer(new int[]{0, 0, grid[0][0]});
for (int i = 0; i < k; i++) {
int threshold = queriesIndices[i][0], index = queriesIndices[i][1];
while (!pq.isEmpty() && pq.peek()[2] < threshold) {
points++;
int[] arr = pq.poll();
int row = arr[0], col = arr[1];
for (int[] dir : dirs) {
int newRow = row + dir[0], newCol = col + dir[1];
if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && !visited[newRow][newCol]) {
visited[newRow][newCol] = true;
pq.offer(new int[]{newRow, newCol, grid[newRow][newCol]});
}
}
}
answer[index] = points;
}
return answer;
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| public class Solution {
static int[][] dirs = {new int[]{-1, 0}, new int[]{1, 0}, new int[]{0, -1}, new int[]{0, 1} };
public int[] MaxPoints(int[][] grid, int[] queries) {
int k = queries.Length;
int[][] queriesIndices = new int[k][];
for (int i = 0; i < k; i++) {
queriesIndices[i] = new int[2];
queriesIndices[i][0] = queries[i];
queriesIndices[i][1] = i;
}
Array.Sort(queriesIndices, (a, b) => a[0] - b[0]);
int[] answer = new int[k];
int points = 0;
int m = grid.Length, n = grid[0].Length;
bool[][] visited = new bool[m][];
for (int i = 0; i < m; i++) {
visited[i] = new bool[n];
}
visited[0][0] = true;
PriorityQueue<int[], int> pq = new PriorityQueue<int[], int>();
pq.Enqueue(new int[]{0, 0, grid[0][0]}, grid[0][0]);
for (int i = 0; i < k; i++) {
int threshold = queriesIndices[i][0], index = queriesIndices[i][1];
while (pq.Count > 0 && pq.Peek()[2] < threshold) {
points++;
int[] arr = pq.Dequeue();
int row = arr[0], col = arr[1];
foreach (int[] dir in dirs) {
int newRow = row + dir[0], newCol = col + dir[1];
if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && !visited[newRow][newCol]) {
visited[newRow][newCol] = true;
pq.Enqueue(new int[]{newRow, newCol, grid[newRow][newCol]}, grid[newRow][newCol]);
}
}
}
answer[index] = points;
}
return answer;
}
}
|
复杂度分析
时间复杂度:O(mn \log (mn) + k \log k),其中 m 和 n 分别是矩阵的行数和列数,k 是数组 queries 的长度。创建查询的新数组并排序的时间是 O(k \log k),广度优先搜索的状态数是 O(mn),每个状态最多加入优先队列和从优先队列取出各一次,每次优先队列操作的时间是 O(\log (mn)),因此广度优先搜索的时间是 O(mn \log (mn)),时间复杂度是 O(mn \log (mn) + k \log k)。
空间复杂度:O(mn + k),其中 m 和 n 分别是矩阵的行数和列数,k 是数组 queries 的长度。创建查询的新数组并排序的空间是 O(k),广度优先搜索的记录每个状态是否访问的二维数组和优先队列的空间是 O(mn),因此空间复杂度是 O(mn + k)。
解法二
思路和算法
使用并查集实现时,需要维护并查集的每个集合的大小,对于每个查询将相应集合的大小作为查询结果。
为了按查询值递增顺序计算每个查询的分数,需要按单元格值递增的顺序遍历每个单元格。需要新建一个单元格数组存储每个单元格的行列下标和单元格值,将单元格数组按单元格值升序排序。
将查询数组和单元格数组排序之后,同时遍历查询数组和单元格数组,计算每个查询的结果。以下描述中,查询数组和单元格数组均为排序后的数组,查询数组的下标为 i,单元格数组的下标为 j,初始时 i = j = 0。
对于第 i 个查询 q_i,应首先将矩阵中的每一对值都小于 q_i 的单元格合并,然后计算从左上角单元格开始可以移动到的值小于 q_i 的单元格的数目。具体做法如下。
当单元格数组的第 j 个元素的单元格值小于 q_i 时,判断单元格数组的第 j 个元素的单元格的所有相邻单元格,如果相邻单元格的单元格值小于 q_i 则将相邻单元格与当前单元格合并,然后将 j 加 1,重复该操作直到 j 超出单元格数组的下标范围或单元格数组的第 j 个元素的单元格值大于等于 q_i。
如果 grid}[0][0] < q_i,则将左上角单元格所属集合的大小作为第 i 个查询的结果;如果 grid}[0][0] \ge q_i,则从左上角单元格开始无法移动到任何单元格,第 i 个查询的结果是 0。将第 i 个查询的结果填到结果数组的相应下标处。
将查询数组和单元格数组排序之后,当遍历到第 i 个查询 q_i 时,可以确保每一对值都小于 q_i 的相邻单元格都合并且其余每一对相邻单元格都未合并,因此查询结果即为从左上角单元格开始可以移动到的值小于 q_i 的单元格的数目。
代码
[sol2-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
| class Solution {
static int[][] dirs = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };
public int[] maxPoints(int[][] grid, int[] queries) {
int k = queries.length;
int[][] queriesIndices = new int[k][2];
for (int i = 0; i < k; i++) {
queriesIndices[i][0] = queries[i];
queriesIndices[i][1] = i;
}
Arrays.sort(queriesIndices, (a, b) -> a[0] - b[0]);
int[] answer = new int[k];
int m = grid.length, n = grid[0].length;
int total = m * n;
int[][] gridArr = new int[total][3];
for (int i = 0; i < total; i++) {
int row = i / n, col = i % n;
gridArr[i][0] = row;
gridArr[i][1] = col;
gridArr[i][2] = grid[row][col];
}
Arrays.sort(gridArr, (a, b) -> a[2] - b[2]);
UnionFind uf = new UnionFind(total);
for (int i = 0, j = 0; i < k; i++) {
int threshold = queriesIndices[i][0], index = queriesIndices[i][1];
while (j < total && gridArr[j][2] < threshold) {
int row = gridArr[j][0], col = gridArr[j][1];
for (int[] dir : dirs) {
int newRow = row + dir[0], newCol = col + dir[1];
if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && grid[newRow][newCol] < threshold) {
uf.union(row * n + col, newRow * n + newCol);
}
}
j++;
}
if (grid[0][0] < threshold) {
answer[index] = uf.getArea(0);
}
}
return answer;
}
}
class UnionFind {
private int[] parent;
private int[] rank;
private int[] area;
public UnionFind(int n) {
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
rank = new int[n];
area = new int[n];
Arrays.fill(area, 1);
}
public void union(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty) {
if (rank[rootx] > rank[rooty]) {
parent[rooty] = rootx;
area[rootx] += area[rooty];
} else if (rank[rootx] < rank[rooty]) {
parent[rootx] = rooty;
area[rooty] += area[rootx];
} else {
parent[rooty] = rootx;
rank[rootx]++;
area[rootx] += area[rooty];
}
}
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
public int getArea(int x) {
return area[find(x)];
}
}
|
[sol2-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
| public class Solution {
static int[][] dirs = {new int[]{-1, 0}, new int[]{1, 0}, new int[]{0, -1}, new int[]{0, 1} };
public int[] MaxPoints(int[][] grid, int[] queries) {
int k = queries.Length;
int[][] queriesIndices = new int[k][];
for (int i = 0; i < k; i++) {
queriesIndices[i] = new int[2];
queriesIndices[i][0] = queries[i];
queriesIndices[i][1] = i;
}
Array.Sort(queriesIndices, (a, b) => a[0] - b[0]);
int[] answer = new int[k];
int m = grid.Length, n = grid[0].Length;
int total = m * n;
int[][] gridArr = new int[total][];
for (int i = 0; i < total; i++) {
gridArr[i] = new int[3];
int row = i / n, col = i % n;
gridArr[i][0] = row;
gridArr[i][1] = col;
gridArr[i][2] = grid[row][col];
}
Array.Sort(gridArr, (a, b) => a[2] - b[2]);
UnionFind uf = new UnionFind(total);
for (int i = 0, j = 0; i < k; i++) {
int threshold = queriesIndices[i][0], index = queriesIndices[i][1];
while (j < total && gridArr[j][2] < threshold) {
int row = gridArr[j][0], col = gridArr[j][1];
foreach (int[] dir in dirs) {
int newRow = row + dir[0], newCol = col + dir[1];
if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && grid[newRow][newCol] < threshold) {
uf.Union(row * n + col, newRow * n + newCol);
}
}
j++;
}
if (grid[0][0] < threshold) {
answer[index] = uf.GetArea(0);
}
}
return answer;
}
}
class UnionFind {
private int[] parent;
private int[] rank;
private int[] area;
public UnionFind(int n) {
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
rank = new int[n];
area = new int[n];
Array.Fill(area, 1);
}
public void Union(int x, int y) {
int rootx = Find(x);
int rooty = Find(y);
if (rootx != rooty) {
if (rank[rootx] > rank[rooty]) {
parent[rooty] = rootx;
area[rootx] += area[rooty];
} else if (rank[rootx] < rank[rooty]) {
parent[rootx] = rooty;
area[rooty] += area[rootx];
} else {
parent[rooty] = rootx;
rank[rootx]++;
area[rootx] += area[rooty];
}
}
}
public int Find(int x) {
if (parent[x] != x) {
parent[x] = Find(parent[x]);
}
return parent[x];
}
public int GetArea(int x) {
return area[Find(x)];
}
}
|
复杂度分析
时间复杂度:O(mn \log (mn) + k \log k + (mn + k) \times \alpha(mn)),其中 m 和 n 分别是矩阵的行数和列数,k 是数组 queries 的长度,\alpha 是反阿克曼函数。创建查询的新数组并排序的时间是 O(k \log k),创建单元格数组并排序的时间是 O(mn \log (mn)),并查集的初始化的时间是 O(mn),计算查询结果的过程中需要执行 mn 次合并操作和 k 次查找操作,这里的并查集使用了路径压缩和按秩合并,单次操作的时间复杂度是 O(\alpha(mn)),因此时间复杂度是 O(mn \log (mn) + k \log k + (mn + k) \times \alpha(mn))。
空间复杂度:O(mn + k),其中 m 和 n 分别是矩阵的行数和列数,k 是数组 queries 的长度。创建查询的新数组并排序的空间是 O(k),创建单元格数组并排序的空间是 O(mn),并查集的空间是 O(mn),因此空间复杂度是 O(mn + k)。