2536-子矩阵元素加 1
给你一个正整数 n ,表示最初有一个 n x n 、下标从 0 开始的整数矩阵 mat ,矩阵中填满了 0 。
另给你一个二维整数数组 query 。针对每个查询 query[i] = [row1i, col1i, row2i, col2i]
,请你执行下述操作:
- 找出 左上角 为
(row1i, col1i)且 右下角 为(row2i, col2i)的子矩阵,将子矩阵中的 每个元素 加1。也就是给所有满足row1i <= x <= row2i和col1i <= y <= col2i的mat[x][y]加1。
返回执行完所有操作后得到的矩阵 mat 。
示例 1:
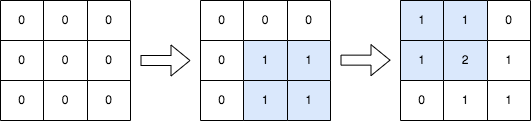
**输入:** n = 3, queries = [[1,1,2,2],[0,0,1,1]]
**输出:** [[1,1,0],[1,2,1],[0,1,1]]
**解释:** 上图所展示的分别是:初始矩阵、执行完第一个操作后的矩阵、执行完第二个操作后的矩阵。
- 第一个操作:将左上角为 (1, 1) 且右下角为 (2, 2) 的子矩阵中的每个元素加 1 。
- 第二个操作:将左上角为 (0, 0) 且右下角为 (1, 1) 的子矩阵中的每个元素加 1 。
示例 2:

**输入:** n = 2, queries = [[0,0,1,1]]
**输出:** [[1,1],[1,1]]
**解释:** 上图所展示的分别是:初始矩阵、执行完第一个操作后的矩阵。
- 第一个操作:将矩阵中的每个元素加 1 。
提示:
1 <= n <= 5001 <= queries.length <= 1040 <= row1i <= row2i < n0 <= col1i <= col2i < n
这个题可以用标准的二维差分来做:
对所有的查询,首先维护二维差分数组;然后对差分数组求前缀和即为答案。
如果不熟悉二维差分,可以参考我的这篇 题解 。下面的说明摘自我之前的题解。
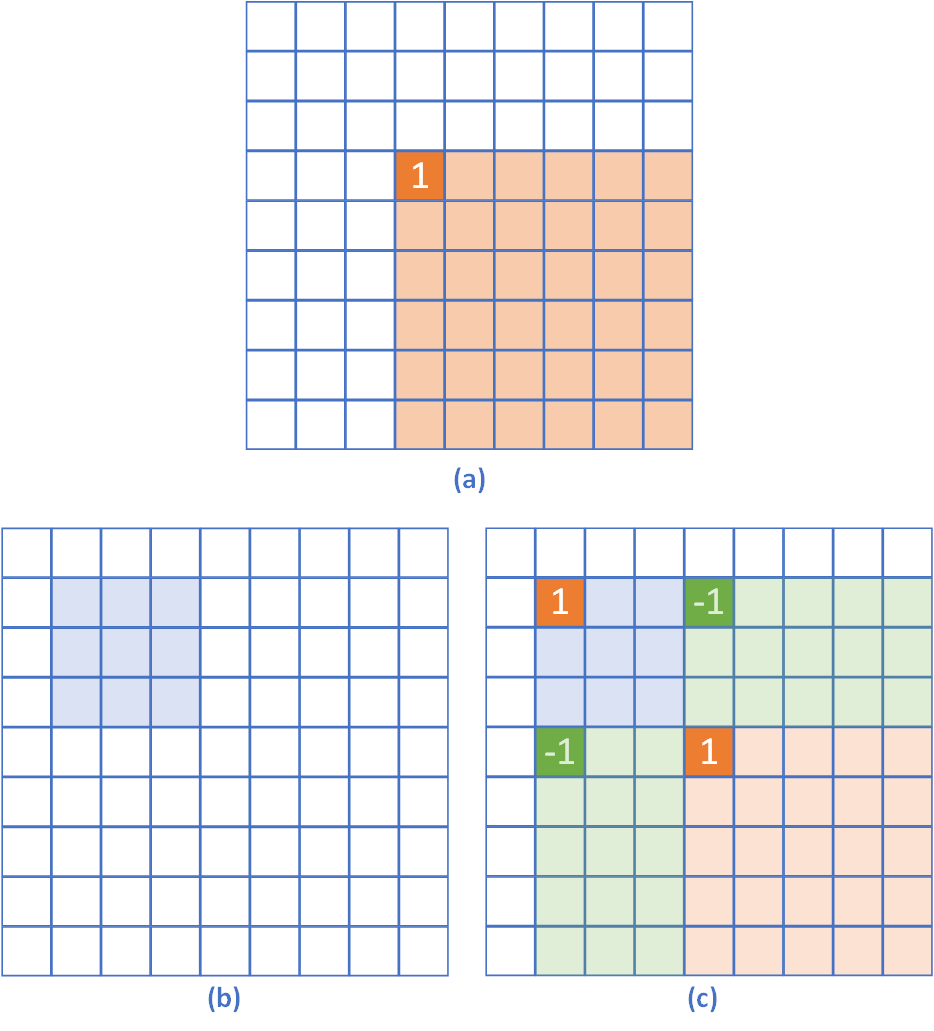
如果将矩阵的第 (i,j) 个单元格中的值增加 1,那么,若对矩阵求二维前缀和,那么下图 (a) 中的黄色区域的值都会增加 1。
如果要将矩阵中的 任意 矩形区域(如下图中 (b) 的蓝色区域)的值增加 1 呢?只需按照下图 (c) 来修改矩阵即可。修改后,若对矩阵求前缀和,那么,只会有蓝色的区域的值 +1,其它区域的值都不变。
1 | class Solution { |
Comments