2538-最大价值和与最小价值和的差值

给你一个 n 个节点的无向无根图，节点编号为 0 到 n - 1 。给你一个整数 n 和一个长度为 n - 1 的二维整数数组
edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。

每个节点都有一个价值。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价值。

一条路径的 价值和 是这条路径上所有节点的价值之和。

你可以选择树中任意一个节点作为根节点 root 。选择 root 为根的 开销 是以 root 为起点的所有路径中， 价值和
最大的一条路径与最小的一条路径的差值。

请你返回所有节点作为根节点的选择中， 最大 的 开销 为多少。

示例 1：

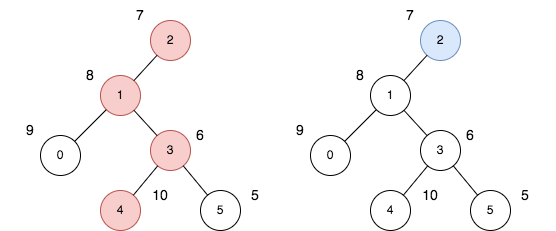
**输入：** n = 6, edges = [[0,1],[1,2],[1,3],[3,4],[3,5]], price = [9,8,7,6,10,5]
**输出：** 24
**解释：** 上图展示了以节点 2 为根的树。左图（红色的节点）是最大价值和路径，右图（蓝色的节点）是最小价值和路径。
- 第一条路径节点为 [2,1,3,4]：价值为 [7,8,6,10] ，价值和为 31 。
- 第二条路径节点为 [2] ，价值为 [7] 。
最大路径和与最小路径和的差值为 24 。24 是所有方案中的最大开销。

示例 2：

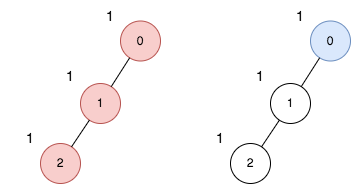
**输入：** n = 3, edges = [[0,1],[1,2]], price = [1,1,1]
**输出：** 2
**解释：** 上图展示了以节点 0 为根的树。左图（红色的节点）是最大价值和路径，右图（蓝色的节点）是最小价值和路径。
- 第一条路径包含节点 [0,1,2]：价值为 [1,1,1] ，价值和为 3 。
- 第二条路径节点为 [0] ，价值为 [1] 。
最大路径和与最小路径和的差值为 2 。2 是所有方案中的最大开销。

提示：

• 1 <= n <= 105
• edges.length == n - 1
• 0 <= ai, bi <= n - 1
• edges 表示一棵符合题面要求的树。
• price.length == n
• 1 <= price[i] <= 105

提示 1

由于价值都是正数，因此价值和最小的一条路径一定只有一个点。

提示 2

根据提示 1，「价值和最大的一条路径与最小的一条路径的差值」等价于「去掉路径的一个端点」。

提示 3

由于价值都是正数，一条路径能延长就尽量延长，这样路径和就越大，那么最优是延长到叶子。

根据提示 2，问题转换成去掉一个叶子后的最大路径和（这里的叶子严格来说是度为 1 的点，因为根的度数也可能是 1）。

提示 4

最大路径和是一个经典树形 DP 问题，类似「树的直径」。由于我们需要去掉一个叶子，那么可以让子树返回两个值：

• 带叶子的最大路径和；
• 不带叶子的最大路径和。

对于当前节点，它有多颗子树，我们一颗颗 DFS，假设当前 DFS 完了其中一颗子树，它返回了「当前带叶子的路径和」和「当前不带叶子的路径和」，那么答案有两种情况：

• 前面最大带叶子的路径和 + 当前不带叶子的路径和；
• 前面最大不带叶子的路径和 + 当前带叶子的路径和；

然后更新「最大带叶子的路径和」和「最大不带叶子的路径和」。

最后返回「最大带叶子的路径和」和「最大不带叶子的路径和」，用来供父节点计算。

附：视频讲解 。

[sol1-Python3]

class Solution:
    def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:
        g = [[] for _ in range(n)]
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)  # 建树

        ans = 0
        # 返回带叶子的最大路径和，不带叶子的最大路径和
        def dfs(x: int, fa: int) -> (int, int):
            nonlocal ans
            max_s1 = p = price[x]
            max_s2 = 0
            for y in g[x]:
                if y == fa: continue
                s1, s2 = dfs(y, x)
                # 前面最大带叶子的路径和 + 当前不带叶子的路径和
                # 前面最大不带叶子的路径和 + 当前带叶子的路径和
                ans = max(ans, max_s1 + s2, max_s2 + s1)
                max_s1 = max(max_s1, s1 + p)
                max_s2 = max(max_s2, s2 + p)  # 这里加上 p 是因为 x 必然不是叶子
            return max_s1, max_s2
        dfs(0, -1)
        return ans

[sol1-Java]

class Solution {
    private List<Integer>[] g;
    private int[] price;
    private long ans;

    public long maxOutput(int n, int[][] edges, int[] price) {
        this.price = price;
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (var e : edges) {
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x); // 建树
        }
        dfs(0, -1);
        return ans;
    }

    // 返回带叶子的最大路径和，不带叶子的最大路径和
    private long[] dfs(int x, int fa) {
        long p = price[x], maxS1 = p, maxS2 = 0;
        for (var y : g[x])
            if (y != fa) {
                var res = dfs(y, x);
                long s1 = res[0], s2 = res[1];
                // 前面最大带叶子的路径和 + 当前不带叶子的路径和
                // 前面最大不带叶子的路径和 + 当前带叶子的路径和
                ans = Math.max(ans, Math.max(maxS1 + s2, maxS2 + s1));
                maxS1 = Math.max(maxS1, s1 + p);
                maxS2 = Math.max(maxS2, s2 + p); // 这里加上 p 是因为 x 必然不是叶子
            }
        return new long[]{maxS1, maxS2};
    }
}

[sol1-C++]

class Solution {
public:
    long long maxOutput(int n, vector<vector<int>> &edges, vector<int> &price) {
        vector<vector<int>> g(n);
        for (auto &e : edges) {
            int x = e[0], y = e[1];
            g[x].push_back(y);
            g[y].push_back(x); // 建树
        }

        long ans = 0;
        // 返回带叶子的最大路径和，不带叶子的最大路径和
        function<pair<long, long>(int, int)> dfs = [&](int x, int fa) -> pair<long, long> {
            long p = price[x], max_s1 = p, max_s2 = 0;
            for (int y : g[x])
                if (y != fa) {
                    auto[s1, s2] = dfs(y, x);
                    // 前面最大带叶子的路径和 + 当前不带叶子的路径和
                    // 前面最大不带叶子的路径和 + 当前带叶子的路径和
                    ans = max(ans, max(max_s1 + s2, max_s2 + s1));
                    max_s1 = max(max_s1, s1 + p);
                    max_s2 = max(max_s2, s2 + p); // 这里加上 p 是因为 x 必然不是叶子
                }
            return {max_s1, max_s2};
        };
        dfs(0, -1);
        return ans;
    }
};

[sol1-Go]

func maxOutput(n int, edges [][]int, price []int) int64 {
	ans := 0
	g := make([][]int, n)
	for _, e := range edges {
		x, y := e[0], e[1]
		g[x] = append(g[x], y)
		g[y] = append(g[y], x) // 建树
	}
	// 返回带叶子的最大路径和，不带叶子的最大路径和
	var dfs func(int, int) (int, int)
	dfs = func(x, fa int) (int, int) {
		p := price[x]
		maxS1, maxS2 := p, 0
		for _, y := range g[x] {
			if y != fa {
				s1, s2 := dfs(y, x)
				// 前面最大带叶子的路径和 + 当前不带叶子的路径和
				// 前面最大不带叶子的路径和 + 当前带叶子的路径和
				ans = max(ans, max(maxS1+s2, maxS2+s1))
				maxS1 = max(maxS1, s1+p)
				maxS2 = max(maxS2, s2+p) // 这里加上 p 是因为 x 必然不是叶子
			}
		}
		return maxS1, maxS2
	}
	dfs(0, -1)
	return int64(ans)
}

func max(a, b int) int { if b > a { return b }; return a }

复杂度分析

• 时间复杂度：O(n)。
• 空间复杂度：O(n)。

相似题目

• 124. 二叉树中的最大路径和
• 1245. 树的直径
• 2246. 相邻字符不同的最长路径