2556-二进制矩阵中翻转最多一次使路径不连通
给你一个下标从 0 开始的 m x n 二进制 矩阵 grid 。你可以从一个格子 (row, col) 移动到格子(row + 1, col) 或者 (row, col + 1) ,前提是前往的格子值为 1 。如果从 (0, 0) 到 (m - 1, n - 1) 没有任何路径,我们称该矩阵是 不连通 的。
你可以翻转 最多一个 格子的值(也可以不翻转)。你 不能翻转 格子 (0, 0) 和 (m - 1, n - 1) 。
如果可以使矩阵不连通,请你返回 true ,否则返回 _ _false _ _ 。
注意 ,翻转一个格子的值,可以使它的值从 0 变 1 ,或从 1 变 0 。
示例 1:
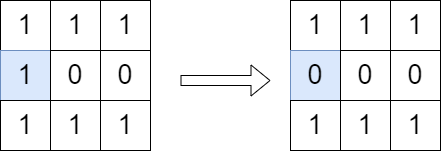
**输入:** grid = [[1,1,1],[1,0,0],[1,1,1]]
**输出:** true
**解释:** 按照上图所示我们翻转蓝色格子里的值,翻转后从 (0, 0) 到 (2, 2) 没有路径。
示例 2:
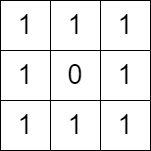
**输入:** grid = [[1,1,1],[1,0,1],[1,1,1]]
**输出:** false
**解释:** 无法翻转至多一个格子,使 (0, 0) 到 (2, 2) 没有路径。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10001 <= m * n <= 105grid[0][0] == grid[m - 1][n - 1] == 1
提示 1
如果让你把所有从起点到终点的路径上的格子都做个标记,这些标记的「轮廓」会是什么样的?
如果可以使矩阵不连通,「轮廓」应该有什么特点?
提示 2
如果可以使矩阵不连通,那么你翻转的那个格子必然会使「轮廓」也不连通(断开)。
如何找到「轮廓」?
提示 3
从 (0,0) 出发,优先向下走,其次向右走,得到下轮廓。
从 (0,0) 出发,优先向右走,其次向下走,得到上轮廓。
如果两个轮廓有交集(除了起点终点),那么翻转交集中的任意一个格子,都可以使矩阵不连通。
代码实现时,可以直接把下轮廓的格子值修改成 0,如果再从 (0,0) 出发,无法到达终点,则说明可以使矩阵不连通。也就是说,得到下轮廓后,无需求上轮廓,只需要看 (0,0) 和终点之间是否有通路即可。
附:视频讲解
1 | class Solution: |
1 | class Solution { |
1 | class Solution { |
1 | func isPossibleToCutPath(g [][]int) bool { |
复杂度分析
- 时间复杂度:O(mn),其中 m 为 grid 的长度,n 为 grid}[i] 的长度。
- 空间复杂度:O(m+n)。递归需要 O(m+n) 的栈空间。
思考题
如果题目还允许向上和向左,要如何做呢?
欢迎在评论区发表你的做法。
如果你觉得自己的思维能力有些薄弱,可以做做 从周赛中学算法 - 2022 年周赛题目总结(下篇) 中的「思维题」这节,所有题目我都写了题解。
Comments