2602-使数组元素全部相等的最少操作次数
给你一个正整数数组 nums 。
同时给你一个长度为 m 的整数数组 queries 。第 i 个查询中,你需要将 nums 中所有元素变成 queries[i]
。你可以执行以下操作 任意 次:
- 将数组里一个元素 增大 或者 减小
1。
请你返回一个长度为 m 的数组 _ _answer ,其中 _ _answer[i]是将 nums 中所有元素变成 queries[i]
的 最少 操作次数。
注意 ,每次查询后,数组变回最开始的值。
示例 1:
**输入:** nums = [3,1,6,8], queries = [1,5]
**输出:** [14,10]
**解释:** 第一个查询,我们可以执行以下操作:
- 将 nums[0] 减小 2 次,nums = [1,1,6,8] 。
- 将 nums[2] 减小 5 次,nums = [1,1,1,8] 。
- 将 nums[3] 减小 7 次,nums = [1,1,1,1] 。
第一个查询的总操作次数为 2 + 5 + 7 = 14 。
第二个查询,我们可以执行以下操作:
- 将 nums[0] 增大 2 次,nums = [5,1,6,8] 。
- 将 nums[1] 增大 4 次,nums = [5,5,6,8] 。
- 将 nums[2] 减小 1 次,nums = [5,5,5,8] 。
- 将 nums[3] 减小 3 次,nums = [5,5,5,5] 。
第二个查询的总操作次数为 2 + 4 + 1 + 3 = 10 。
示例 2:
**输入:** nums = [2,9,6,3], queries = [10]
**输出:** [20]
**解释:** 我们可以将数组中所有元素都增大到 10 ,总操作次数为 8 + 1 + 4 + 7 = 20 。
提示:
n == nums.lengthm == queries.length1 <= n, m <= 1051 <= nums[i], queries[i] <= 109
本题视频讲解
见【周赛 338】 。
前置知识:前缀和
对于数组 nums,定义它的前缀和 s}[0]=0,s}[i+1] = \sum\limits_{j=0}^{i}\textit{nums}[j]。
根据这个定义,有 s[i+1]=s[i]+\textit{nums}[i]。
例如 nums}=[1,2,-1,2],对应的前缀和数组为 s=[0,1,3,2,4]。
通过前缀和,我们可以把子数组的元素和转换成两个前缀和的差,即
\sum_{j=\textit{left} }^{\textit{right} }\textit{nums}[j] = \sum\limits_{j=0}^{\textit{right} }\textit{nums}[j] - \sum\limits_{j=0}^{\textit{left}-1}\textit{nums}[j] = \textit{s}[\textit{right}+1] - \textit{s}[\textit{left}]
例如 nums 的子数组 [2,-1,2] 的和就可以用 s[4]-s[1]=4-1=3 算出来。
注:为方便计算,常用左闭右开区间 [\textit{left},\textit{right}) 来表示从 nums}[\textit{left}] 到 nums}[\textit{right}-1] 的子数组,此时子数组的和为 s}[\textit{right}] - \textit{s}[\textit{left}],子数组的长度为 right}-\textit{left。
注 2:s[0]=0 表示一个空数组的元素和。为什么要额外定义它?想一想,如果要计算的子数组恰好是一个前缀(从 nums}[0] 开始),你要用 s[\textit{right}] 减去谁呢?通过定义 s[0]=0,任意子数组(包括前缀)都可以表示为两个前缀和的差。
前置知识:二分查找
见【基础算法精讲 04】 。
思路
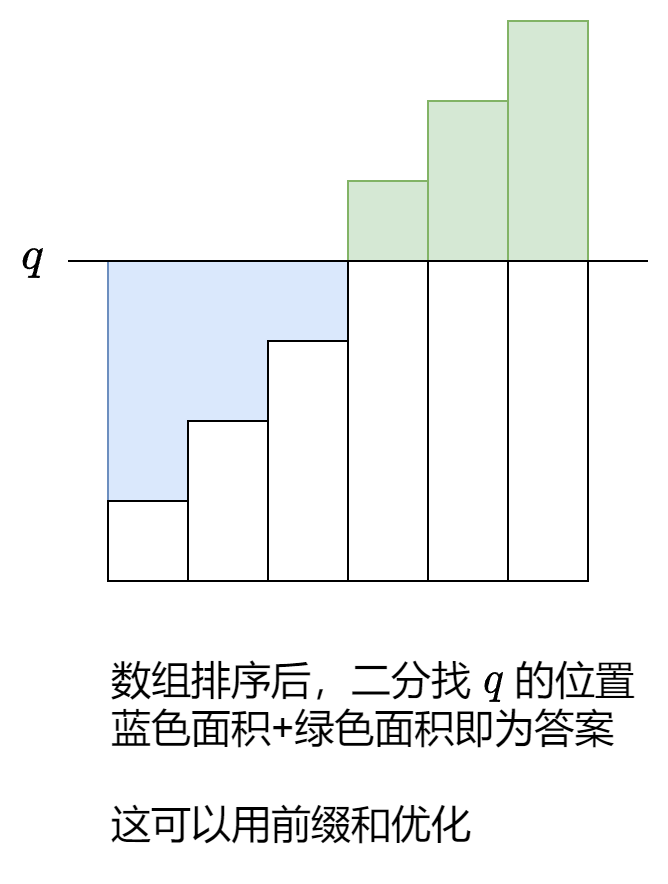
1 | class Solution: |
1 | class Solution { |
1 | class Solution { |
1 | func minOperations(nums, queries []int) []int64 { |
复杂度分析
- 时间复杂度:O((n+q)\log n),其中 n 为 nums 的长度,q 为 queries 的长度。
- 空间复杂度:O(n)。返回值不计入。