2603-收集树中金币

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:27 2023-09-13 16:06:27 Updated    

给你一个 n 个节点的无向无根树，节点编号从 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组
edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。再给你一个长度为 n 的数组
coins ，其中 coins[i] 可能为 0 也可能为 1 ，1 表示节点 i 处有一个金币。

一开始，你需要选择树中任意一个节点出发。你可以执行下述操作任意次：

  • 收集距离当前节点距离为 2 以内的所有金币，或者
  • 移动到树中一个相邻节点。

你需要收集树中所有的金币，并且回到出发节点，请你返回最少经过的边数。

如果你多次经过一条边，每一次经过都会给答案加一。

示例 1：

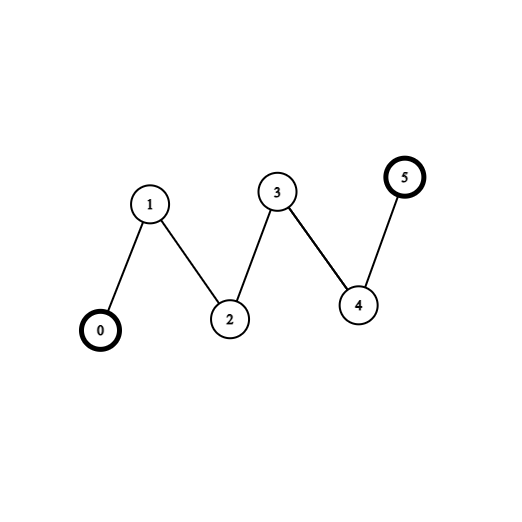
**输入：** coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]]
**输出：** 2
**解释：** 从节点 2 出发，收集节点 0 处的金币，移动到节点 3 ，收集节点 5 处的金币，然后移动回节点 2 。

示例 2：

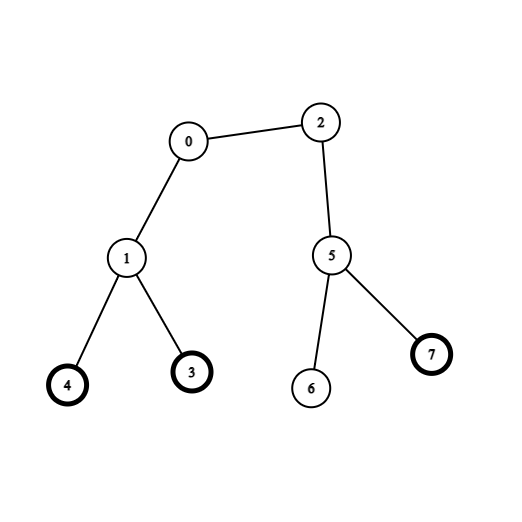
**输入：** coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]]
**输出：** 2
**解释：** 从节点 0 出发，收集节点 4 和 3 处的金币，移动到节点 2 处，收集节点 7 处的金币，移动回节点 0 。

提示：

  • n == coins.length
  • 1 <= n <= 3 * 104
  • 0 <= coins[i] <= 1
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • edges 表示一棵合法的树。

本题视频讲解

见【周赛 338】 25:04。

前置知识：拓扑排序

见【周赛 308】 21:55。

提示 1

去掉不包含金币的子树，访问其中任何一个点都毫无意义。

做法：从没有金币的叶子出发，跑拓扑排序。

注意，去掉这些子树后，某些原来不是叶子的节点会变成叶子。

提示 2

只需要考虑有金币的的叶子，因为不在叶子上的金币顺路就能收集到。

提示 3

从有金币的的叶子出发，再次跑拓扑排序。在拓扑排序的同时，标记每个点入队的时间 time。

注意是入队的时间，不是访问到这个节点的时间。

  • 叶子入队的时间为 0；
  • 去掉这些叶子后，又产生了新的叶子，这些叶子入队的时间为 1；
  • 去掉这些叶子后，又产生了新的叶子，这些叶子入队的时间为 2；
  • ……

示例 2 如下图，数字表示节点入队的时间：

t4.png

那么只要走到 time}[x]=2 的节点 x，就能收集到在叶子上的金币。

遍历所有边 x-y，如果满足 time}[x]\ge 2 且 time}[y]\ge 2（上图蓝色边），那么这条边需要恰好经过 2 次（因为需要回到出发点），答案加 2；如果不满足，则无需经过。

注：从任意被蓝色边连接的点出发，算出来的答案都是一样的。

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution:
    def collectTheCoins(self, coins: List[int], edges: List[List[int]]) -> int:
        n = len(coins)
        g = [[] for _ in range(n)]
        deg = [0] * n
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)  # 建图
            deg[x] += 1
            deg[y] += 1

        # 用拓扑排序「剪枝」：去掉没有金币的子树
        q = deque()
        for i, (d, c) in enumerate(zip(deg, coins)):
            if d == 1 and c == 0:  # 无金币叶子
                q.append(i)
        while q:
            for y in g[q.popleft()]:
                deg[y] -= 1
                if deg[y] == 1 and coins[y] == 0:
                    q.append(y)

        # 再次拓扑排序
        for i, (d, c) in enumerate(zip(deg, coins)):
            if d == 1 and c:  # 有金币叶子
                q.append(i)
        if len(q) <= 1:  # 至多一个有金币的叶子，直接收集
            return 0
        time = [0] * n
        while q:
            x = q.popleft()
            for y in g[x]:
                deg[y] -= 1
                if deg[y] == 1:
                    time[y] = time[x] + 1  # 记录入队时间
                    q.append(y)

        # 统计答案
        return sum(time[x] >= 2 and time[y] >= 2 for x, y in edges) * 2
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {
    public int collectTheCoins(int[] coins, int[][] edges) {
        int n = coins.length;
        List<Integer> g[] = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        var deg = new int[n];
        for (var e : edges) {
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x); // 建图
            ++deg[x];
            ++deg[y];
        }

        // 用拓扑排序「剪枝」：去掉没有金币的子树
        var q = new ArrayDeque<Integer>();
        for (int i = 0; i < n; ++i)
            if (deg[i] == 1 && coins[i] == 0) // 无金币叶子
                q.add(i);
        while (!q.isEmpty()) {
            int x = q.peek();
            q.pop();
            for (int y : g[x])
                if (--deg[y] == 1 && coins[y] == 0)
                    q.add(y);
        }

        // 再次拓扑排序
        for (int i = 0; i < n; ++i)
            if (deg[i] == 1 && coins[i] == 1) // 有金币叶子
                q.add(i);
        if (q.size() <= 1) return 0; // 至多一个有金币的叶子，直接收集
        var time = new int[n];
        while (!q.isEmpty()) {
            int x = q.peek();
            q.pop();
            for (int y : g[x])
                if (--deg[y] == 1) {
                    time[y] = time[x] + 1; // 记录入队时间
                    q.add(y);
                }
        }

        // 统计答案
        int ans = 0;
        for (var e : edges)
            if (time[e[0]] >= 2 && time[e[1]] >= 2)
                ans += 2;
        return ans;
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {
public:
    int collectTheCoins(vector<int> &coins, vector<vector<int>> &edges) {
        int n = coins.size();
        vector<vector<int>> g(n);
        int deg[n]; memset(deg, 0, sizeof(deg));
        for (auto &e: edges) {
            int x = e[0], y = e[1];
            g[x].push_back(y);
            g[y].push_back(x); // 建图
            ++deg[x];
            ++deg[y];
        }

        // 用拓扑排序「剪枝」：去掉没有金币的子树
        queue<int> q;
        for (int i = 0; i < n; ++i)
            if (deg[i] == 1 && coins[i] == 0) // 无金币叶子
                q.push(i);
        while (!q.empty()) {
            int x = q.front();
            q.pop();
            for (int y: g[x])
                if (--deg[y] == 1 && coins[y] == 0)
                    q.push(y);
        }

        // 再次拓扑排序
        for (int i = 0; i < n; ++i)
            if (deg[i] == 1 && coins[i]) // 有金币叶子
                q.push(i);
        if (q.size() <= 1) return 0; // 至多一个有金币的叶子，直接收集
        int time[n]; memset(time, 0, sizeof(time));
        while (!q.empty()) {
            int x = q.front();
            q.pop();
            for (int y: g[x])
                if (--deg[y] == 1) {
                    time[y] = time[x] + 1; // 记录入队时间
                    q.push(y);
                }
        }

        // 统计答案
        int ans = 0;
        for (auto &e: edges)
            if (time[e[0]] >= 2 && time[e[1]] >= 2)
                ans += 2;
        return ans;
    }
};
[sol1-Go]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
func collectTheCoins(coins []int, edges [][]int) (ans int) {
	n := len(coins)
	g := make([][]int, n)
	deg := make([]int, n)
	for _, e := range edges {
		x, y := e[0], e[1]
		g[x] = append(g[x], y)
		g[y] = append(g[y], x) // 建图
		deg[x]++
		deg[y]++
	}

	// 用拓扑排序「剪枝」：去掉没有金币的子树
	q := make([]int, 0, n)
	for i, d := range deg {
		if d == 1 && coins[i] == 0 { // 无金币叶子
			q = append(q, i)
		}
	}
	for len(q) > 0 {
		x := q[0]
		q = q[1:]
		for _, y := range g[x] {
			deg[y]--
			if deg[y] == 1 && coins[y] == 0 {
				q = append(q, y)
			}
		}
	}

	// 再次拓扑排序
	for i, d := range deg {
		if d == 1 && coins[i] == 1 { // 有金币叶子
			q = append(q, i)
		}
	}
	if len(q) <= 1 { // 至多一个有金币的叶子，直接收集
		return
	}
	time := make([]int, n)
	for len(q) > 0 {
		x := q[0]
		q = q[1:]
		for _, y := range g[x] {
			deg[y]--
			if deg[y] == 1 {
				time[y] = time[x] + 1 // 记录入队时间
				q = append(q, y)
			}
		}
	}

	// 统计答案
	for _, e := range edges {
		if time[e[0]] >= 2 && time[e[1]] >= 2 {
			ans += 2
		}
	}
	return
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 为 coins 的长度。
  • 空间复杂度：O(n)。

思考题

如果把题目中的 2 换成 0,1,2,3,\cdots, n-1，你能把这些情况对应的答案全部算出来吗？

见本题视频讲解。

相似题目

 Comments
On this page
2603-收集树中金币
  1. 本题视频讲解
  2. 前置知识：拓扑排序
  3. 提示 1
  4. 提示 2
  5. 提示 3
  6. 复杂度分析
  7. 思考题
  8. 相似题目