2608-图中的最短环

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 17:01:07 2023-09-13 17:01:07 Updated    

现有一个含 n 个顶点的 双向 图，每个顶点按从 0 到 n - 1 标记。图中的边由二维整数数组 edges 表示，其中
edges[i] = [ui, vi] 表示顶点 ui 和 vi 之间存在一条边。每对顶点最多通过一条边连接，并且不存在与自身相连的顶点。

返回图中 最短 环的长度。如果不存在环，则返回 -1 。

环 是指以同一节点开始和结束，并且路径中的每条边仅使用一次。

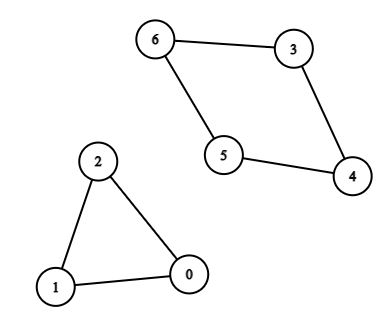
示例 1：

**输入：** n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]]
**输出：** 3
**解释：** 长度最小的循环是：0 -> 1 -> 2 -> 0

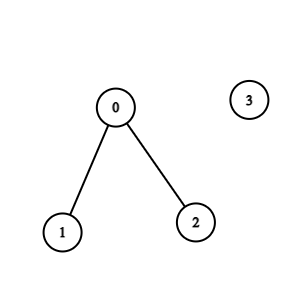
示例 2：

**输入：** n = 4, edges = [[0,1],[0,2]]
**输出：** -1
**解释：** 图中不存在循环

提示：

  • 2 <= n <= 1000
  • 1 <= edges.length <= 1000
  • edges[i].length == 2
  • 0 <= ui, vi < n
  • ui != vi
  • 不存在重复的边

本题视频讲解

见【双周赛 101】 。

思路

b101_t4_cut.png

答疑

问：为什么说发现一个已经入队的点，就说明有环？

答：这说明到同一个点有两条不同的路径，这两条路径组成了一个环。

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:
        g = [[] for _ in range(n)]
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)  # 建图

        def bfs(start: int) -> int:
            ans = inf
            dis = [-1] * n  # dis[i] 表示从 start 到 i 的最短路长度
            dis[start] = 0
            q = deque([(start, -1)])
            while q:
                x, fa = q.popleft()
                for y in g[x]:
                    if dis[y] < 0:  # 第一次遇到
                        dis[y] = dis[x] + 1
                        q.append((y, x))
                    elif y != fa:  # 第二次遇到
                        ans = min(ans, dis[x] + dis[y] + 1)
            return ans

        ans = min(bfs(i) for i in range(n))
        return ans if ans < inf else -1
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    private List<Integer>[] g;
    private int[] dis; // dis[i] 表示从 start 到 i 的最短路长度

    public int findShortestCycle(int n, int[][] edges) {
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (var e : edges) {
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x); // 建图
        }
        dis = new int[n];

        int ans = Integer.MAX_VALUE;
        for (int i = 0; i < n; ++i) // 枚举每个起点跑 BFS
            ans = Math.min(ans, bfs(i));
        return ans < Integer.MAX_VALUE ? ans : -1;
    }

    private int bfs(int start) {
        int ans = Integer.MAX_VALUE;
        Arrays.fill(dis, -1);
        dis[start] = 0;
        var q = new ArrayDeque<int[]>();
        q.add(new int[]{start, -1});
        while (!q.isEmpty()) {
            var p = q.poll();
            int x = p[0], fa = p[1];
            for (int y : g[x])
                if (dis[y] < 0) { // 第一次遇到
                    dis[y] = dis[x] + 1;
                    q.add(new int[]{y, x});
                } else if (y != fa) // 第二次遇到
                    ans = Math.min(ans, dis[x] + dis[y] + 1);
        }
        return ans;
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    int findShortestCycle(int n, vector<vector<int>> &edges) {
        vector<vector<int>> g(n);
        for (auto &e: edges) {
            int x = e[0], y = e[1];
            g[x].push_back(y);
            g[y].push_back(x); // 建图
        }

        int dis[n]; // dis[i] 表示从 start 到 i 的最短路长度
        auto bfs = [&](int start) -> int {
            int ans = INT_MAX;
            memset(dis, -1, sizeof(dis));
            dis[start] = 0;
            queue<pair<int, int>> q;
            q.emplace(start, -1);
            while (!q.empty()) {
                auto [x, fa] = q.front();
                q.pop();
                for (int y: g[x])
                    if (dis[y] < 0) { // 第一次遇到
                        dis[y] = dis[x] + 1;
                        q.emplace(y, x);
                    } else if (y != fa) // 第二次遇到
                        ans = min(ans, dis[x] + dis[y] + 1);
            }
            return ans;
        };
        int ans = INT_MAX;
        for (int i = 0; i < n; ++i) // 枚举每个起点跑 BFS
            ans = min(ans, bfs(i));
        return ans < INT_MAX ? ans : -1;
    }
};
[sol1-Go]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
func findShortestCycle(n int, edges [][]int) int {
	g := make([][]int, n)
	for _, e := range edges {
		x, y := e[0], e[1]
		g[x] = append(g[x], y)
		g[y] = append(g[y], x) // 建图
	}

	ans := math.MaxInt
	dis := make([]int, n) // dis[i] 表示从 start 到 i 的最短路长度
	for start := 0; start < n; start++ { // 枚举每个起点跑 BFS
		for j := range dis {
			dis[j] = -1
		}
		dis[start] = 0
		type pair struct{ x, fa int }
		q := []pair{ {start, -1} }
		for len(q) > 0 {
			p := q[0]
			q = q[1:]
			x, fa := p.x, p.fa
			for _, y := range g[x] {
				if dis[y] < 0 { // 第一次遇到
					dis[y] = dis[x] + 1
					q = append(q, pair{y, x})
				} else if y != fa { // 第二次遇到
					ans = min(ans, dis[x]+dis[y]+1)
				}
			}
		}
	}
	if ans == math.MaxInt { // 无环图
		return -1
	}
	return ans
}

func min(a, b int) int { if b < a { return b }; return a }

复杂度分析

  • 时间复杂度：O(nm)，其中 m 为 edges 的长度。每次 BFS 需要 O(m) 的时间。
  • 空间复杂度：O(n+m)。

思考题

如果改成求最大环要怎么做？

极端情况下，这会算出一个哈密顿回路，而它是 NP 完全问题，只能通过爆搜得到。

 Comments
On this page
2608-图中的最短环
  1. 本题视频讲解
  2. 思路
  3. 答疑
  4. 复杂度分析
  5. 思考题