给你一个下标从 0 开始的 m x n 整数矩阵 grid 。你一开始的位置在 左上角 格子 (0, 0) 。
当你在格子 (i, j) 的时候,你可以移动到以下格子之一:
满足 j < k <= grid[i][j] + j 的格子 (i, k) (向右移动),或者
满足 i < k <= grid[i][j] + i 的格子 (k, j) (向下移动)。
请你返回到达 右下角 格子 (m - 1, n - 1) 需要经过的最少移动格子数,如果无法到达右下角格子,请你返回 -1 。
示例 1:
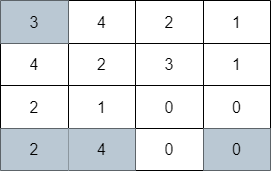
**输入:** grid = [[3,4,2,1],[4,2,3,1],[2,1,0,0],[2,4,0,0]]
**输出:** 4
**解释:** 上图展示了到达右下角格子经过的 4 个格子。
示例 2:
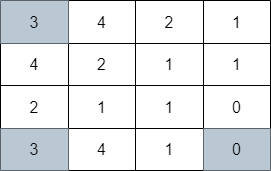
**输入:** grid = [[3,4,2,1],[4,2,1,1],[2,1,1,0],[3,4,1,0]]
**输出:** 3
**解释:** 上图展示了到达右下角格子经过的 3 个格子。
示例 3:
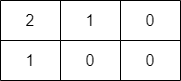
**输入:** grid = [[2,1,0],[1,0,0]]
**输出:** -1
**解释:** 无法到达右下角格子。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 1051 <= m * n <= 1050 <= grid[i][j] < m * ngrid[m - 1][n - 1] == 0
算法
首先这道题只能向下或者向右走,所以我们可以直接用二重循环来算答案,省去例如 bfs 之类的框架。
当我们在位置 (i, j) 时,如何计算到达该位置的最少移动次数呢?我们可以考虑上一步是向下还是向右走的。例如是「向下走」的,那么上一个位置应该是 (i’, j),其中 i’ < i。除此之外,i’ 还需要满足什么要求呢?可以想到有下面两个要求:
(i’, j) 要能走到 (i, j);
到达 (i’, j) 的移动次数要最小。
根据第二个要求,我们可以想到使用「优先队列」来维护所有的 i’,堆顶为移动次数最少的位置;同时根据第一个要求,我们可以在获取堆顶时进行判断,如果堆顶的 i’ 不满足要求,就可以将它永久从优先队列中移除,因为之后共享同一列 j 的位置 i 只会更大,更不可能走到。
因此,我们对于每一列都维护一个优先队列。第 j 个优先队列存储的是所有位于第 j 列的位置,优先队列中存储两个值,第一个值为到达 (i’, j) 最少的移动次数,作为比较的关键字;第二个值为 i’。
同理,我们对于每一行也维护一个优先队列,这样就可以处理「向右走」的情况了。
代码
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 class Solution {private : using PII = pair<int , int >; using ChatGPT = priority_queue<PII, vector<PII>, greater<PII>>; public : int minimumVisitedCells (vector<vector<int >>& grid) int m = grid.size (), n = grid[0 ].size (); vector<vector<int >> dist (m, vector <int >(n, -1 )); dist[0 ][0 ] = 1 ; vector<ChatGPT> row (m) , col (n) ; auto update = [](int & x, int y) { if (x == -1 || x > y) { x = y; } }; for (int i = 0 ; i < m; ++i) { for (int j = 0 ; j < n; ++j) { while (!row[i].empty () && row[i].top ().second + grid[i][row[i].top ().second] < j) { row[i].pop (); } if (!row[i].empty ()) { update (dist[i][j], dist[i][row[i].top ().second] + 1 ); } while (!col[j].empty () && col[j].top ().second + grid[col[j].top ().second][j] < i) { col[j].pop (); } if (!col[j].empty ()) { update (dist[i][j], dist[col[j].top ().second][j] + 1 ); } if (dist[i][j] != -1 ) { row[i].emplace (dist[i][j], j); col[j].emplace (dist[i][j], i); } } } return dist[m - 1 ][n - 1 ]; } };
[sol1-Python] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution : def minimumVisitedCells (self, grid: List [List [int ]] ) -> int : m, n = len (grid), len (grid[0 ]) dist = [[-1 ] * n for _ in range (m)] dist[0 ][0 ] = 1 row, col = [[] for _ in range (m)], [[] for _ in range (n)] def update (x: int , y: int ) -> int : return y if x == -1 or x > y else x for i in range (m): for j in range (n): while row[i] and row[i][0 ][1 ] + grid[i][row[i][0 ][1 ]] < j: heapq.heappop(row[i]) if row[i]: dist[i][j] = update(dist[i][j], dist[i][row[i][0 ][1 ]] + 1 ) while col[j] and col[j][0 ][1 ] + grid[col[j][0 ][1 ]][j] < i: heapq.heappop(col[j]) if col[j]: dist[i][j] = update(dist[i][j], dist[col[j][0 ][1 ]][j] + 1 ) if dist[i][j] != -1 : heapq.heappush(row[i], (dist[i][j], j)) heapq.heappush(col[j], (dist[i][j], i)) return dist[m - 1 ][n - 1 ]
复杂度分析
时间复杂度:O(mn \cdot (\log m + \log n))。
空间复杂度:O(mn)。