给你一棵二叉树的根 root ,请你将每个节点的值替换成该节点的所有 **堂兄弟节点值的和 **。
如果两个节点在树中有相同的深度且它们的父节点不同,那么它们互为 堂兄弟 。
请你返回修改值之后,树的根 _ _root _ _ 。
注意 ,一个节点的深度指的是从树根节点到这个节点经过的边数。
示例 1:

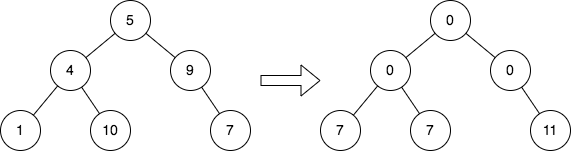
**输入:** root = [5,4,9,1,10,null,7]
**输出:** [0,0,0,7,7,null,11]
**解释:** 上图展示了初始的二叉树和修改每个节点的值之后的二叉树。
- 值为 5 的节点没有堂兄弟,所以值修改为 0 。
- 值为 4 的节点没有堂兄弟,所以值修改为 0 。
- 值为 9 的节点没有堂兄弟,所以值修改为 0 。
- 值为 1 的节点有一个堂兄弟,值为 7 ,所以值修改为 7 。
- 值为 10 的节点有一个堂兄弟,值为 7 ,所以值修改为 7 。
- 值为 7 的节点有两个堂兄弟,值分别为 1 和 10 ,所以值修改为 11 。
示例 2:

**输入:** root = [3,1,2]
**输出:** [0,0,0]
**解释:** 上图展示了初始的二叉树和修改每个节点的值之后的二叉树。
- 值为 3 的节点没有堂兄弟,所以值修改为 0 。
- 值为 1 的节点没有堂兄弟,所以值修改为 0 。
- 值为 2 的节点没有堂兄弟,所以值修改为 0 。
提示:
- 树中节点数目的范围是
[1, 105] 。
1 <= Node.val <= 104
本题视频讲解
见【双周赛 102】 第三题。
前置知识:二叉树的 BFS(层序遍历)
见【基础算法精讲 13】 。
提示 1
下文将具有相同父节点的节点互称为兄弟节点。
对于一个节点 x 来说,它的所有堂兄弟节点值的和,等价于 x 这一层的所有节点值之和,减去 x 及其兄弟节点的值之和。
例如样例 1:
- 4 的左右儿子的节点值,都被更新成了 7,也就是左右儿子这一层的节点值之和 1+10+7=18,减去 4 的左右儿子的节点值之和 1+10=11,得到 7。
- 9 的右儿子的节点值,被更新成了 11,也就是右儿子这一层的节点值之和 1+10+7=18,减去 9 的右儿子的节点值 7,得到 11。
提示 2
怎么实现呢?
用 BFS 遍历二叉树,对于每一层:
- 首先,遍历当前层的每个节点,通过节点的左右儿子,计算下一层的节点值之和 nextLevelSum;
- 然后,再次遍历当前层的每个节点 x,计算 x 的左右儿子的节点值之和 childrenSum,更新 x 的左右儿子的节点值为 nextLevelSum}-\textit{childrenSum。
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution:
def replaceValueInTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
root.val = 0
q = [root]
while q:
tmp = q
q = []
next_level_sum = 0
for node in tmp:
if node.left:
q.append(node.left)
next_level_sum += node.left.val
if node.right:
q.append(node.right)
next_level_sum += node.right.val
for node in tmp:
children_sum = (node.left.val if node.left else 0) + \
(node.right.val if node.right else 0)
if node.left: node.left.val = next_level_sum - children_sum
if node.right: node.right.val = next_level_sum - children_sum
return root
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public TreeNode replaceValueInTree(TreeNode root) {
root.val = 0;
var q = new ArrayList<TreeNode>();
q.add(root);
while (!q.isEmpty()) {
var tmp = q;
q = new ArrayList<>();
int nextLevelSum = 0;
for (var node : tmp) {
if (node.left != null) {
q.add(node.left);
nextLevelSum += node.left.val;
}
if (node.right != null) {
q.add(node.right);
nextLevelSum += node.right.val;
}
}
for (var node : tmp) {
int childrenSum = (node.left != null ? node.left.val : 0) +
(node.right != null ? node.right.val : 0);
if (node.left != null) node.left.val = nextLevelSum - childrenSum;
if (node.right != null) node.right.val = nextLevelSum - childrenSum;
}
}
return root;
}
}
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public:
TreeNode *replaceValueInTree(TreeNode *root) {
root->val = 0;
vector<TreeNode*> q = {root};
while (!q.empty()) {
vector<TreeNode*> nxt;
int next_level_sum = 0;
for (auto node: q) {
if (node->left) {
nxt.push_back(node->left);
next_level_sum += node->left->val;
}
if (node->right) {
nxt.push_back(node->right);
next_level_sum += node->right->val;
}
}
for (auto node: q) {
int children_sum = (node->left ? node->left->val : 0) +
(node->right ? node->right->val : 0);
if (node->left) node->left->val = next_level_sum - children_sum;
if (node->right) node->right->val = next_level_sum - children_sum;
}
q = move(nxt);
}
return root;
}
};
|
[sol1-Go]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| func replaceValueInTree(root *TreeNode) *TreeNode {
root.Val = 0
q := []*TreeNode{root}
for len(q) > 0 {
tmp := q
q = nil
nextLevelSum := 0
for _, node := range tmp {
if node.Left != nil {
q = append(q, node.Left)
nextLevelSum += node.Left.Val
}
if node.Right != nil {
q = append(q, node.Right)
nextLevelSum += node.Right.Val
}
}
for _, node := range tmp {
childrenSum := 0
if node.Left != nil {
childrenSum += node.Left.Val
}
if node.Right != nil {
childrenSum += node.Right.Val
}
if node.Left != nil {
node.Left.Val = nextLevelSum - childrenSum
}
if node.Right != nil {
node.Right.Val = nextLevelSum - childrenSum
}
}
}
return root
}
|
复杂度分析
- 时间复杂度:O(n),其中 n 为二叉树的节点个数。
- 空间复杂度:O(n)。