2673-使二叉树所有路径值相等的最小代价

给你一个整数 n 表示一棵 满二叉树 里面节点的数目，节点编号从 1 到 n 。根节点编号为 1 ，树中每个非叶子节点 i
都有两个孩子，分别是左孩子 2 * i 和右孩子 2 * i + 1 。

树中每个节点都有一个值，用下标从 ** 0** 开始、长度为 n 的整数数组 cost 表示，其中 cost[i] 是第 i + 1
个节点的值。每次操作，你可以将树中任意节点的值增加 1 。你可以执行操作任意次。

你的目标是让根到每一个 叶子结点 的路径值相等。请你返回最少需要执行增加操作多少次。

注意：

满二叉树 指的是一棵树，它满足树中除了叶子节点外每个节点都恰好有 2 个节点，且所有叶子节点距离根节点距离相同。
路径值 指的是路径上所有节点的值之和。

示例 1：

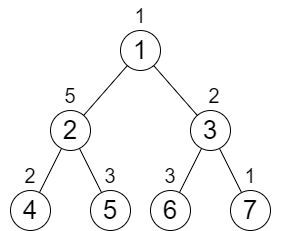
**输入：** n = 7, cost = [1,5,2,2,3,3,1]
**输出：** 6
**解释：** 我们执行以下的增加操作：
- 将节点 4 的值增加一次。
- 将节点 3 的值增加三次。
- 将节点 7 的值增加两次。
从根到叶子的每一条路径值都为 9 。
总共增加次数为 1 + 3 + 2 = 6 。
这是最小的答案。

示例 2：

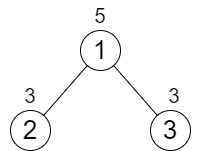
**输入：** n = 3, cost = [5,3,3]
**输出：** 0
**解释：** 两条路径已经有相等的路径值，所以不需要执行任何增加操作。

提示：

3 <= n <= 105
n + 1 是 2 的幂
cost.length == n
1 <= cost[i] <= 104

本题视频讲解

见【周赛 344】第四题，欢迎点赞投币！

提示 1

考虑根到两个互为兄弟节点的叶子的两条路径。

由于这两条路径除了叶子节点不一样，其余节点都一样，所以为了让这两条路径的路径和相等，必须修改叶子节点的值。

设叶子节点的值分别为 x 和 y，假设 x\le y，是否需要同时增加 x 和 y 呢？

这是不需要的，把 x 增加 y-x 就行，因为我们可以增加它们的祖先节点的值，使得它们俩的路径和与其它的路径和相等，这样可以节省操作次数。

提示 2

对于不是叶子的兄弟节点，又要如何比较和计算呢？

和上面的分析一样，从根到当前节点的路径，除了这两个兄弟节点不一样，其余节点都一样。所以把路径和从叶子往上传，这样就可以按照提示 1 那样比较了。

示例 1 如下图，节点 2 的路径和视作 x+5+3=x+8，节点 3 的路径和视作 x+2+3=x+5（其中 x 是上面的路径和），这样可以知道需要把节点 3 的值增加 (x+8)-(x+5)=8-5=3。

代码实现时，可以直接在 cost 上累加路径和。由于 cost 的下标是从 0 开始的，所以代码中的节点编号转成 cost 下标，都需要减一。

[sol1-Python3]class Solution:
    def minIncrements(self, n: int, cost: List[int]) -> int:
        ans = 0
        for i in range(n // 2, 0, -1):  # 从最后一个非叶节点开始算
            ans += abs(cost[i * 2 - 1] - cost[i * 2])  # 两个子节点变成一样的
            cost[i - 1] += max(cost[i * 2 - 1], cost[i * 2])  # 累加路径和
        return ans

[sol1-Java]class Solution {
    public int minIncrements(int n, int[] cost) {
        int ans = 0;
        for (int i = n / 2; i > 0; i--) { // 从最后一个非叶节点开始算
            ans += Math.abs(cost[i * 2 - 1] - cost[i * 2]); // 两个子节点变成一样的
            cost[i - 1] += Math.max(cost[i * 2 - 1], cost[i * 2]); // 累加路径和
        }
        return ans;
    }
}

[sol1-C++]class Solution {
public:
    int minIncrements(int n, vector<int> &cost) {
        int ans = 0;
        for (int i = n / 2; i; i--) { // 从最后一个非叶节点开始算
            ans += abs(cost[i * 2 - 1] - cost[i * 2]); // 两个子节点变成一样的
            cost[i - 1] += max(cost[i * 2 - 1], cost[i * 2]); // 累加路径和
        }
        return ans;
    }
};

[sol1-Go]func minIncrements(n int, cost []int) (ans int) {
	for i := n / 2; i > 0; i-- { // 从最后一个非叶节点开始算
		left, right := cost[i*2-1], cost[i*2]
		if left > right { // 保证 left <= right
			left, right = right, left
		}
		ans += right - left // 两个子节点变成一样的
		cost[i-1] += right // 累加路径和
	}
	return
}

复杂度分析

时间复杂度：\mathcal{O}(n)，其中 n 为 cost 的长度。
空间复杂度：\mathcal{O}(1)。仅用到若干额外变量。

思考题

如果可以对节点值减一要怎么做？