2718-查询后矩阵的和

给你一个整数 n 和一个下标从 0 开始的 二维数组 queries ，其中 queries[i] = [typei, indexi, vali] 。

一开始，给你一个下标从 0 开始的 n x n 矩阵，所有元素均为 0 。每一个查询，你需要执行以下操作之一：

• 如果 typei == 0 ，将第 indexi 行的元素全部修改为 vali ，覆盖任何之前的值。
• 如果 typei == 1 ，将第 indexi 列的元素全部修改为 vali ，覆盖任何之前的值。

请你执行完所有查询以后，返回矩阵中所有整数的和。

示例 1：

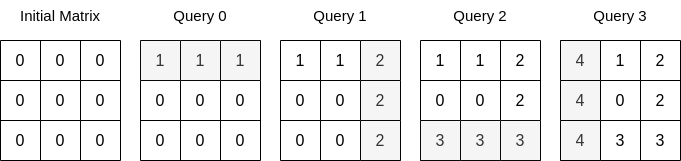
**输入：** n = 3, queries = [[0,0,1],[1,2,2],[0,2,3],[1,0,4]]
**输出：** 23
**解释：** 上图展示了每个查询以后矩阵的值。所有操作执行完以后，矩阵元素之和为 23 。

示例 2：

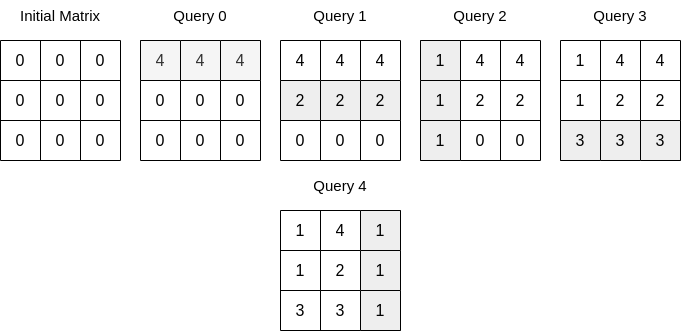
**输入：** n = 3, queries = [[0,0,4],[0,1,2],[1,0,1],[0,2,3],[1,2,1]]
**输出：** 17
**解释：** 上图展示了每一个查询操作之后的矩阵。所有操作执行完以后，矩阵元素之和为 17 。

提示：

• 1 <= n <= 104
• 1 <= queries.length <= 5 * 104
• queries[i].length == 3
• 0 <= typei <= 1
• 0 <= indexi < n
• 0 <= vali <= 105

视频讲解

见【周赛 348】 第三题，欢迎点赞投币！

提示 1

如果对同一行反复操作，那么只有最后一次对这行的操作会计入答案。列同理。

提示 2

正难则反，倒序操作 queries。

提示 3

以行为例。如果 queries}[i] 操作的是行，那么需要知道：

1. 这一行之前有没有操作过（这里「之前」指大于 i 的操作）。对此可以用哈希表 visRow 记录被操作过的行号，哈希表 visCol 记录被操作过的列号。
2. 这一行有多少列之前操作过，这就是 visCol 的长度 m。那么剩余可以填入的格子为 n-m，答案增加了 (n-m)\cdot \textit{val}_i。

这样可以做到 \mathcal{O}(q) 的时间复杂度（与 n 无关）。

代码实现时，可以把 visRow 和 visCol 放到一个长为 2 的数组中，简化代码逻辑。

[sol-Python3]

class Solution:
    def matrixSumQueries(self, n: int, queries: List[List[int]]) -> int:
        ans = 0
        vis = [set(), set()]
        for type, index, val in reversed(queries):
            if index not in vis[type]:  # 后面（>i）没有对这一行/列的操作
                # 这一行/列还剩下 n-len(vis[type^1]) 个可以填入的格子
                ans += (n - len(vis[type ^ 1])) * val
                vis[type].add(index)  # 标记操作过
        return ans

[sol-Java]

class Solution {
    public long matrixSumQueries(int n, int[][] queries) {
        long ans = 0;
        Set<Integer>[] vis = new Set[]{new HashSet<>(), new HashSet<>()};
        for (int i = queries.length - 1; i >= 0; i--) {
            var q = queries[i];
            int type = q[0], index = q[1], val = q[2];
            if (!vis[type].contains(index)) { // 后面（>i）没有对这一行/列的操作
                // 这一行/列还剩下 n-vis[type^1].size() 个可以填入的格子
                ans += (long) (n - vis[type ^ 1].size()) * val;
                vis[type].add(index);
            }
        }
        return ans;
    }
}

[sol-C++]

class Solution {
public:
    long long matrixSumQueries(int n, vector<vector<int>> &queries) {
        long long ans = 0;
        unordered_set<int> vis[2];
        for (int i = queries.size() - 1; i >= 0; i--) {
            auto &q = queries[i];
            int type = q[0], index = q[1], val = q[2];
            if (!vis[type].count(index)) { // 后面（>i）没有对这一行/列的操作
                // 这一行/列还剩下 n-vis[type^1].size() 个可以填入的格子
                ans += (long long) (n - vis[type ^ 1].size()) * val;
                vis[type].insert(index);
            }
        }
        return ans;
    }
};

[sol-Go]

func matrixSumQueries(n int, queries [][]int) (ans int64) {
	vis := [2]map[int]bool{ {}, {} }
	for i := len(queries) - 1; i >= 0; i-- {
		q := queries[i]
		tp, index, val := q[0], q[1], q[2]
		if !vis[tp][index] { // 后面（>i）没有对这一行/列的操作
			// 这一行/列还剩下 n-len(vis[tp^1]) 个可以填入的格子
			ans += int64(n-len(vis[tp^1])) * int64(val)
			vis[tp][index] = true // 标记操作过
		}
	}
	return
}

复杂度分析

• 时间复杂度：\mathcal{O}(q)，其中 q 为 queries 的长度。
• 空间复杂度：\mathcal{O}(\min{q,n})。哈希表中至多有 \mathcal{O}(n) 个数。

相似题目

• 2382. 删除操作后的最大子段和