2791-树中可以形成回文的路径数
给你一棵 树 (即,一个连通、无向且无环的图), 根 节点为 0 ,由编号从 0 到 n - 1 的 n
个节点组成。这棵树用一个长度为 n 、下标从 0 开始的数组 parent 表示,其中 parent[i] 为节点 i
的父节点,由于节点 0 为根节点,所以 parent[0] == -1 。
另给你一个长度为 n 的字符串 s ,其中 s[i] 是分配给 i 和 parent[i] 之间的边的字符。s[0] 可以忽略。
找出满足 u < v ,且从 u 到 v 的路径上分配的字符可以 重新排列 形成 回文 的所有节点对 (u, v)
,并返回节点对的数目。
如果一个字符串正着读和反着读都相同,那么这个字符串就是一个 回文 。
示例 1:
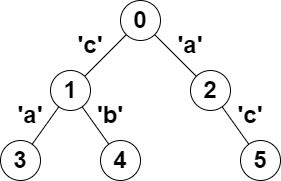
**输入:** parent = [-1,0,0,1,1,2], s = "acaabc"
**输出:** 8
**解释:** 符合题目要求的节点对分别是:
- (0,1)、(0,2)、(1,3)、(1,4) 和 (2,5) ,路径上只有一个字符,满足回文定义。
- (2,3),路径上字符形成的字符串是 "aca" ,满足回文定义。
- (1,5),路径上字符形成的字符串是 "cac" ,满足回文定义。
- (3,5),路径上字符形成的字符串是 "acac" ,可以重排形成回文 "acca" 。
示例 2:
**输入:** parent = [-1,0,0,0,0], s = "aaaaa"
**输出:** 10
**解释:** 任何满足 u < v 的节点对 (u,v) 都符合题目要求。
提示:
n == parent.length == s.length1 <= n <= 105- 对于所有
i >= 1,0 <= parent[i] <= n - 1均成立 parent[0] == -1parent表示一棵有效的树s仅由小写英文字母组成
下午两点【b站@灵茶山艾府】 直播讲题,欢迎关注!
前置知识:位运算
提示 1
回文串等价于至多一个字母出现奇数次,其余字母出现偶数次。
提示 2
用一个长为 26 的二进制数来压缩存储每个字母的奇偶性。
一条边可以看成是 1<<(s[i]-'a')。
那么路径所对应的二进制数,就是路径上的所有边的异或和(因为异或就是模 2 剩余系中的加法,刚好可以表示奇偶性)。
只有 27 个二进制数符合要求:
- 0,表示每个字母都出现偶数次。
- 2^0,2^1,\cdots,2^{25,表示第 i 个字母出现奇数次,其余字母出现偶数次。
提示 3
设 v 和 w 的最近公共祖先为 lca,设从根到 i 的路径异或和为 XOR}_{i。
v 到 w 的路径可以看成是 v-\textit{lca}-w,其中 lca 到 v 的路径异或和,等于根到 v 的异或和,再异或上根到 lca 的异或和(从根到 lca 的边异或了两次,等于 0 抵消掉)。lca 到 w 的路径异或和也同理。
所以 v-\textit{lca}-w 的异或和为
(\textit{XOR}{v} \oplus \textit{XOR}{lca}) \oplus (\textit{XOR}{w} \oplus \textit{XOR}{lca})
XOR}_{lca 异或了两次,抵消掉,所以上式为
\textit{XOR}{v} \oplus \textit{XOR}{w}
把所有 XOR}_i 求出来,就变成判断这 n-1 个数当中:
- 两数异或和是否为 0?这意味着路径上的每个字母都出现偶数次。
- 两数异或和是否为 2 的幂?这意味着路径上恰好有个字母出现奇数次,其余字母出现偶数次。
- 特殊情况:XOR}{i}=0 或者 XOR}{i 为 2 的幂,表示从根到 i 的路径符合要求,我们可以异或上一条「空路径」对应的异或值,即 0,就转换成了上面两数异或和的情况。
这可以用类似两数之和的思路解决,用哈希表记录 XOR}_{i 的个数,设当前算出的异或和为 x,去哈希表中找 x 的出现次数以及 x\oplus 2^k 的出现次数。
1 | class Solution: |
1 | func countPalindromePaths(parent []int, s string) int64 { |
复杂度分析
- 时间复杂度:\mathcal{O}(n),其中 n 为 s 的长度。
- 空间复杂度:\mathcal{O}(n)。