LCP 10-二叉树任务调度

任务调度优化是计算机性能优化的关键任务之一。在任务众多时，不同的调度策略可能会得到不同的总体执行时间，因此寻求一个最优的调度方案是非常有必要的。

通常任务之间是存在依赖关系的，即对于某个任务，你需要先完成他的前导任务（如果非空），才能开始执行该任务。
我们保证任务的依赖关系是一棵二叉树， 其中 root 为根任务，root.left 和 root.right
为他的两个前导任务（可能为空），root.val 为其自身的执行时间。

在一个 CPU
核执行某个任务时，我们可以在任何时刻暂停当前任务的执行，并保留当前执行进度。在下次继续执行该任务时，会从之前停留的进度开始继续执行。暂停的时间可以不是整数。

现在，系统有两个 CPU 核，即我们可以同时执行两个任务，但是同一个任务不能同时在两个核上执行。给定这颗任务树，请求出所有任务执行完毕的最小时间。

示例 1：

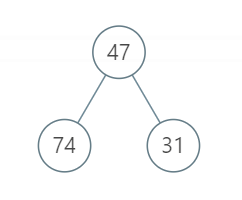![image.png](https://pic.leetcode-
cn.com/3522fbf8ce4ebb20b79019124eb9870109fdfe97fe9da99f6c20c07ceb1c60b3-image.png)

输入：root = [47, 74, 31]

输出：121

解释：根节点的左右节点可以并行执行31分钟，剩下的43+47分钟只能串行执行，因此总体执行时间是121分钟。

示例 2：

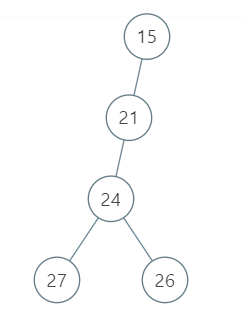![image.png](https://pic.leetcode-
cn.com/13accf172ee4a660d241e25901595d55b759380b090890a17e6e7bd51a143e3f-image.png)

输入：root = [15, 21, null, 24, null, 27, 26]

输出：87

示例 3：

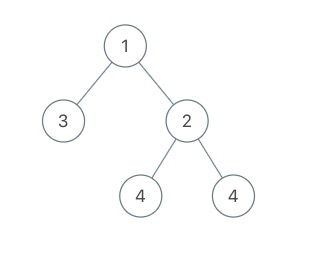![image.png](https://pic.leetcode-
cn.com/bef743a12591aafb9047dd95d335b8083dfa66e8fdedc63f50fd406b4a9d163a-image.png)

输入：root = [1,3,2,null,null,4,4]

输出：7.5

限制：

1 <= 节点数量 <= 1000
1 <= 单节点执行时间 <= 1000

题意概述

有一个二叉树形式的任务依赖结构，我们有两个 CPU 核，这两个核可以同时执行不同的任务，问执行完所有任务的最小时间，也即是希望两个 CPU 核的并行时间尽可能大。

题目解析

这道题虽然代码量很少，但思维难度较高。

在通过对示例的观察后，我们可以得出以下重要结论：

对于任何一颗任务树，它一定有一个先并行后串行的最优策略。树的根结点只能串行。 这个结论的正确性是因为只有在这颗任务树退化成一个链以后，它才不能被并行，所以把串行延后执行不会导致执行时间变长。
设一颗任务树的所有任务时间之和为 x ，最大并行时间为 y ，那么这个任务最少需要 x - y 的时间完成。其中前 y 秒用于并行，后 x - 2y 秒用于串行。注意由于上一条结论，在区间 [x - 2y, x] 内的所有剩余时间都是可以 只通过 并行取到的。对于叶子节点 node 来说，它的任务总时间即为 node.val ，最大并行时间为 0 。

所有任务时间之和很容易求，下面我们求最大并行时间。

解法一

设一颗任务树的左子树所有任务时间和为 a ，最大并行时间为 b ，右子树分别为 c, d 。那么这颗任务树最大并行时间为 a + c}{2，但不一定能取到。

不失一般性，假设 a \geq c 。如果 a - 2b \leq c ，那么最优策略是左树先并行 a - c 的任务，剩余 c 的任务量，然后再两树并行，就达成了一直并行。并行时间取到了 a + c}{2 。

如果 a - 2b > c ，那么剩余 a - 2b - c 的任务无法被并行。并行时间最大为 b + c 。

题解代码

[sol1-Python]# Definition for a binary tree node.
# class ceeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def minimalExecTime(self, root):
        """
        :type root: TreeNode
        :rtype: float
        """
        def dfs(root):
            if root is None:
                return 0., 0.
            tc = root.val
			
            # 先递归左右子树
            a, b = dfs(root.left)
            c, d = dfs(root.right)
            
            tc = tc + a + c
            # 只考虑 a >= c 的情况，不满足就交换
            if a < c:
                a, c = c, a
                b, d = d, b
            
            if a - 2 * b <= c:
                pc = (a + c) / 2
            else:
                pc = c + b

            return tc, pc

        tc, pc = dfs(root)
        return tc - pc

[sol1-C++]/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    pair<int, double> DFS(TreeNode* root) {
        if (!root) return {0, 0.0};
        auto l = DFS(root->left);
        auto r = DFS(root->right);

        int a = l.first, c = r.first;
        double b = l.second, d = r.second;
        int tot = a + c + root->val;
        if ((c - 2 * d <= a && a <= c) || (a - 2 * b <= c && c <= a)) {
            return {tot, (a + c) / 2.0};
        }
        if (a - 2 * b > c) {
            return {tot, b + c};
        } else {
            // c - 2 * d > a
            return {tot, a + d};
        }
    }
    double minimalExecTime(TreeNode* root) {
        auto p = DFS(root);
        return p.first - p.second;
    }
};

复杂度分析

时间复杂度：O(n)。每个节点只被访问一次。
空间复杂度：O(n)。

解法二

虽然解法一已经很清晰了，解法二比解法一更简洁。它的思路是从解法一的基础上得来的。

我们沿用解法一的记号，设一颗任务树的左子树所有任务时间和为 a ，最大并行时间为 b ，右子树分别为 c, d 。不失一般性，假设 a \geq c 。

记这颗任务树的根任务的运行时间为 val 。如果 a - 2b \leq c ，则所有子树上的任务都被并行执行了，所以这颗任务树的最短执行时间为 a + c}{2} + val 。否则，这颗任务树的最短执行时间为 a - b + val 。

通过对以上两种情况的合并，以及考虑到 a < c 的情况，最终我们可以用一个公式直接算出这颗任务树的最短执行时间为

\max(a - b, c - d, a + c}{2}) + val

又由于 a - b, c - d 正好是左右子树的最短执行时间（记为函数 ans ），我们可以进一步简化这个公式：

ans(root) = \max(ans(root.left), ans(root.right), a + c}{2}) + val

使用 DFS 就可以轻松求解了。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    pair<int, double> DFS(TreeNode* root) {
        if (!root) return {0, 0.0};
        auto l = DFS(root->left);
        auto r = DFS(root->right);

        return {l.first + r.first + root->val, root->val + max(max(l.second, r.second), (l.first + r.first) / 2.0)};
    }
    double minimalExecTime(TreeNode* root) {
        auto p = DFS(root);
        return p.second;
    }
};

复杂度分析

时间复杂度：O(n)。每个节点只被访问一次。
空间复杂度：O(n)。