LCP 15-游乐园的迷宫

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:29 2023-09-13 16:06:29 Updated    

小王来到了游乐园，她玩的第一个项目是模拟推销员。有一个二维平面地图，其中散布着 N 个推销点，编号 0 到
N-1，不存在三点共线的情况。每两点之间有一条直线相连。游戏没有规定起点和终点，但限定了每次转角的方向。首先，小王需要先选择两个点分别作为起点和终点，然后从起点开始访问剩余
N-2 个点恰好一次并回到终点。访问的顺序需要满足一串给定的长度为 N-2 由 L 和 R 组成的字符串
direction，表示从起点出发之后在每个顶点上转角的方向。根据这个提示，小王希望你能够帮她找到一个可行的遍历顺序，输出顺序下标（若有多个方案，输出任意一种）。可以证明这样的遍历顺序一定是存在的。

![Screenshot 2020-03-20 at 17.04.58.png](https://pic.leetcode-
cn.com/595b60797d4a461287864a8cd05bba1d3b8760104ff83f43b902fd68477be9c3-Screenshot%202020-03-20%20at%2017.04.58.png)

（上图：A->B->C 右转； 下图：D->E->F 左转）

示例 1：

输入：points = [[1,1],[1,4],[3,2],[2,1]], direction = "LL"

输入：[0,2,1,3]

解释：[0,2,1,3] 是符合”LL”的方案之一。在 [0,2,1,3] 方案中，0->2->1 是左转方向， 2->1->3 也是左转方向
![图片.gif](https://pic.leetcode-
cn.com/c01c1efc423b916267c2a3a170266c925c368d62afa047c267cc1020970e55d9-%E5%9B%BE%E7%89%87.gif)

示例 2：

输入：points = [[1,3],[2,4],[3,3],[2,1]], direction = "LR"

输入：[0,3,1,2]

解释：[0,3,1,2] 是符合”LR”的方案之一。在 [0,3,1,2] 方案中，0->3->1 是左转方向， 3->1->2 是右转方向

限制：

  • 3 <= points.length <= 1000 且 points[i].length == 2
  • 1 <= points[i][0],points[i][1] <= 10000
  • direction.length == points.length - 2
  • direction 只包含 "L","R"

题意概述

平面上有 N 个点，找到一条访问 N 个点的路径，使得路径的转角满足给定的转角序列。

题解

我们保持一个理想的状态：转向时，剩余的点都位于要求方向的一侧（即剩余点都符合当前这次的转向要求）。那么当前这次转向选择什么点，可以使下一次转向依旧满足这个理想的状态，从而可以不断的递归找下去。

若下一次转向的要求方向是 L (R)，则这次转向的点中选择相对方向最右（最左）的点即可。

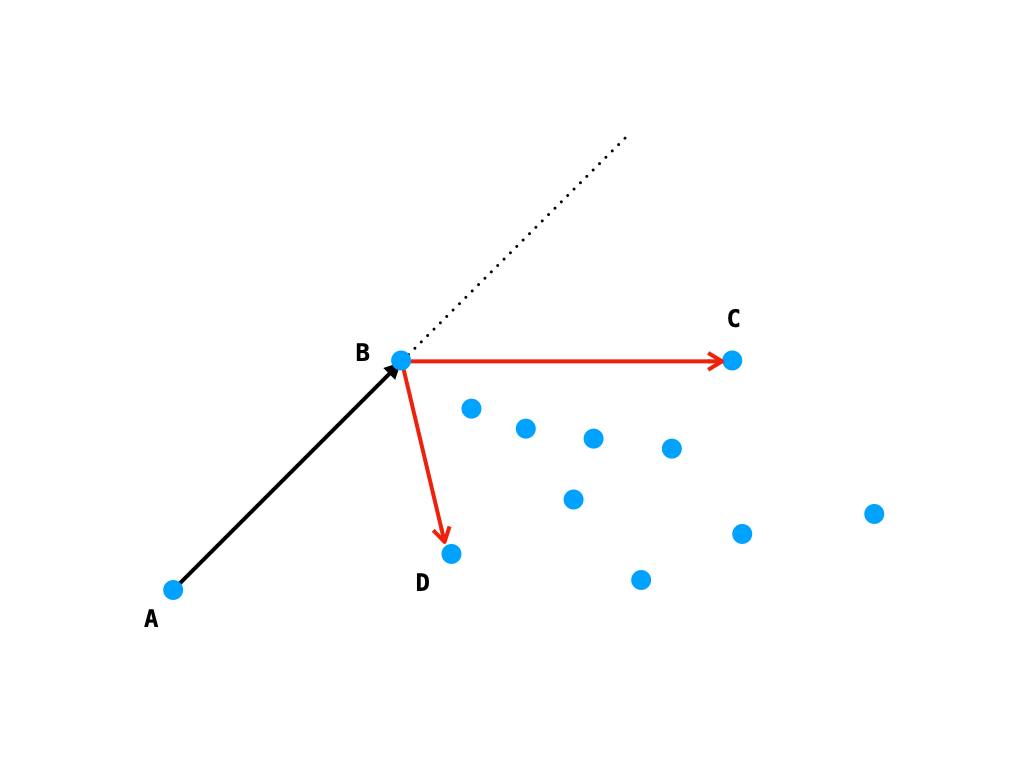
如图所示，当前位于 B 点且转向方向为 R，其余点都位于 \overrightarrow{AB 的右侧，其中点 C、D分别是相对方向最左和最右的点。若下一次转向方向为 L，则这次选择 D 点，可使剩余点都位于 \overrightarrow{BD 的左侧；若下一次转向方向为 R，则这次选择 C 点，可使剩余点都位于 \overrightarrow{BC 的右侧。

fig1

这里的最左或最右的选择，可利用利用叉积的性质：若向量 \overrightarrow{BC 和向量 \overrightarrow{BD 的叉积结果为正，则从向量 \overrightarrow{BC 到向量 \overrightarrow{BD 为逆时针旋转（ \overrightarrow{BD 在 \overrightarrow{BC 的左侧）；反之若结果为负，则从向量 \overrightarrow{BC 到向量 \overrightarrow{BD 为顺时针旋转（ \overrightarrow{BD 在 \overrightarrow{BC 的右侧）。

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
class Solution {
private:
    pair<int, int> Sub(pair<int, int> a, pair<int, int> b) {
        // 求点 a 到点 b 的向量
        return make_pair(a.first - b.first, a.second - b.second);
    }

    int Cross(pair<int, int> a, pair<int, int> b) {
        // 求向量 a 到向量 b 的向量叉积
        return a.first * b.second - a.second * b.first;
    }
public:
    vector<int> visitOrder(vector< vector<int> >& points, string dir) {
        int n = points.size();
        vector<bool> used(n, false);  // 记录点的遍历情况， False未遍历 / True已遍历
        vector< pair<int, int> > point;
        vector<int> order; // 记录返回结果

        for (int i=0; i<n; ++i) {
            point.push_back( make_pair(points[i][0], points[i][1]) );
        }

        // 查找最左的点作为 起始点
        int start = 0;
        for (int i=1; i<n; ++i) {
            if (point[i] < point[start]) {
                start = i;
            }
        }
        used[start] = true;
        order.push_back(start);

        for (int i=0; i<dir.size(); ++i) {
            int next = -1;
            if (dir[i] == 'L') {
                // 转向方向为 L，选择相对方向最右的点
                for (int j=0; j<n; ++j) {
                    if (!used[j]) {
                        if (next == -1 || Cross(Sub(point[next], point[start]), Sub(point[j], point[start])) < 0) {
                            next = j;
                        }
                    } 
                }
            } else if (dir[i] == 'R') {
                // 转向方向为 R，选择相对方向最左的点
                for (int j=0; j<n; ++j) {
                    if (!used[j]) {
                        if (next == -1 || Cross(Sub(point[next], point[start]), Sub(point[j], point[start])) > 0) {
                            next = j;
                        }
                    } 
                }
            }
            // 返回结果加入选择的点，更新下一次转向的起点
            used[next] = true;
            order.push_back(next);
            start = next;
        }
        // 添加最后一个剩余点
        for (int i=0; i<n; ++i) {
            if (used[i] == false) {
                order.push_back(i);
            }
        }
        return order;
    }
};
[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution:
    def sub(self, a, b): # 求点 a 到点 b 的向量
        return [a[0]-b[0], a[1]-b[1]]
    
    def cross(self, a, b):  # 求向量 a 到向量 b 的向量叉积
        return a[0] * b[1] - a[1] * b[0]
    
    def visitOrder(self, points: List[List[int]], direction: str) -> List[int]:
        n = len(points)
        used = [False] * n  # 记录点的遍历情况， False未遍历 / True已遍历
        order = [] # 记录返回结果
        
        # 查找最左的点作为 起始点
        start = 0
        for i in range(0,n):
            if points[i][0] < points[start][0]:
                start = i
        used[start] =True
        order.append(start)
        
        for i in direction:
            nxt = -1
            if i=='L':
                # 转向方向为 L，选择相对方向最右的点
                for j in range(0,n):
                    if not used[j]:
                        if nxt==-1 or self.cross(self.sub(points[nxt],points[start]), self.sub(points[j],points[start])) <0 :
                            nxt = j
            else:
                # 转向方向为 R，选择相对方向最左的点
                for j in range(0,n):
                    if not used[j]:
                        if nxt==-1 or self.cross(self.sub(points[nxt],points[start]), self.sub(points[j],points[start])) >0 :
                            nxt = j
            # 返回结果加入选择的点，更新下一次转向的起点
            used[nxt] = True
            order.append(nxt)
            start = nxt
        
        # 添加最后一个剩余点
        for i in range(0,n):
            if not used[i]:
                order.append(i)
        return order

复杂度分析

  • 时间复杂度：O(N^2)，其中 N 是平面上点的个数。

  • 空间复杂度：O(N)。

 Comments
On this page
LCP 15-游乐园的迷宫
  1. 题意概述
    1. 题解