LCP 21-追逐游戏

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:23 2023-09-13 16:06:23 Updated    

秋游中的小力和小扣设计了一个追逐游戏。他们选了秋日市集景区中的 N 个景点，景点编号为 1~N。此外，他们还选择了 N
条小路，满足任意两个景点之间都可以通过小路互相到达，且不存在两条连接景点相同的小路。整个游戏场景可视作一个无向连通图，记作二维数组 edges，数组中以
[a,b] 形式表示景点 a 与景点 b 之间有一条小路连通。
小力和小扣只能沿景点间的小路移动。小力的目标是在最快时间内追到小扣，小扣的目标是尽可能延后被小力追到的时间。游戏开始前，两人分别站在两个不同的景点
startA 和 startB。每一回合，小力先行动，小扣观察到小力的行动后再行动。小力和小扣在每回合可选择以下行动之一： - 移动至相邻景点
- 留在原地 如果小力追到小扣（即两人于某一时刻出现在同一位置），则游戏结束。若小力可以追到小扣，请返回最少需要多少回合；若小力无法追到小扣，请返回
-1。 注意：小力和小扣一定会采取最优移动策略。 示例 1： >输入：edges = [[1,2],[2,3],[3,4],[4,1],[2,5],[5,6]], startA = 3, startB = 5 > >输出：3 >

解释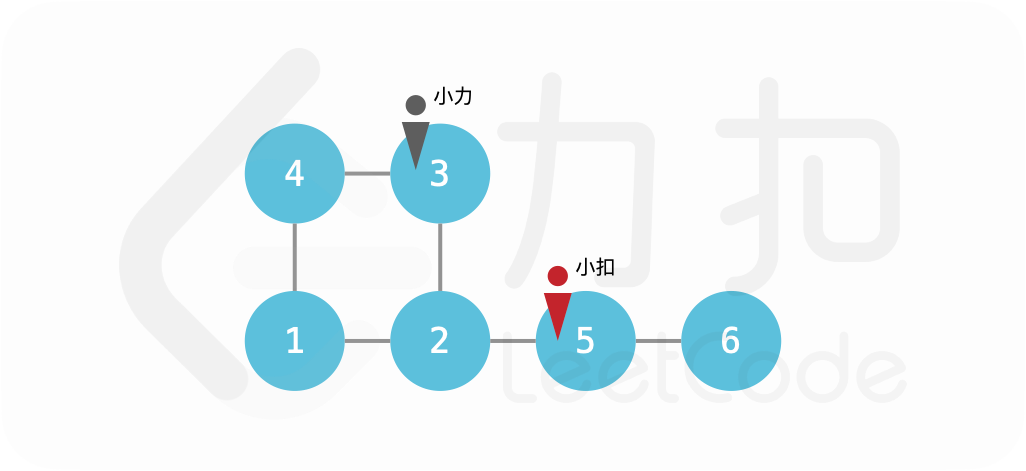： >![image.png](https://pic.leetcode-cn.com/1597991318-goeHHr-
image.png){:height=”250px”} > >第一回合，小力移动至 2 号点，小扣观察到小力的行动后移动至 6 号点；
第二回合，小力移动至 5 号点，小扣无法移动，留在原地； >第三回合，小力移动至 6 号点，小力追到小扣。返回 3。 示例 2：
输入：edges = [[1,2],[2,3],[3,4],[4,1]], startA = 1, startB = 3 > >输出：-1 >
解释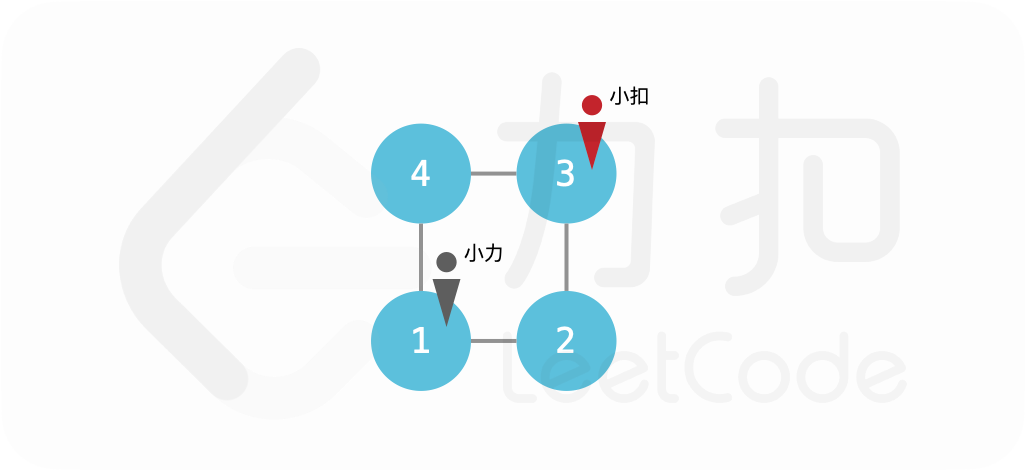： >![image.png](https://pic.leetcode-cn.com/1597991157-QfeakF-
image.png){:height=”250px”} > >小力如果不动，则小扣也不动；否则小扣移动到小力的对角线位置。这样小力无法追到小扣。
提示： - edges 的长度等于图中节点个数 - 3 <= edges.length <= 10^5 - 1 <= edges[i][0], edges[i][1] <= edges.length 且 edges[i][0] != edges[i][1] - 1 <= startA, startB <= edges.length 且 startA != startB

解题思路

本题综合考察了图上的DFS和BFS，有一定的思考价值。

N个节点N条边的连通图，一定有且只有一个环。这是解决本题必须想到的一点。想一想为什么？

接下来，我们就开始分情况讨论了：

  • 如果A、B一开始就相邻（有一条A–B的边），那么A第一回合就直接捉到了B。
  • 否则，我们找到图中唯一的那个环，将环上的点进行标记。
    • 如果环的长度为3，那么这个环并不能让B永远绕着走下去。
    • 如果环的长度大于等于4，我们求出B进入环的位置和需要走的距离，再求出A到这个位置的距离。如果A的距离大于B的距离加一，那么B就可以在环上一直绕下去而不被捉到。
  • 如果环长为3或A可以在环上拦截B，我们需要找出游戏最多进行的回合数。我们求出A和B到图上所有点的距离，然后枚举各个点。
    • 如果A到某个点的距离小于等于B的距离加一，说明A有可能在这个点之前拦截到B，想一想为什么？
    • 否则，B可以移动到这个点，游戏至少需要进行的回合数为A到这个点的距离。
    • 枚举所有点，就可以找到合法的最大距离。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#define INF 0x3f3f3f3f

class Solution {
    vector<vector<int>> adj;
    vector<int> depth, parent;
    vector<bool> in_loop;
    int n, loop = 0;
    void dfs(int u, int p) {
        parent[u] = p;
        depth[u] = depth[p] + 1;
        for (int v : adj[u]) {
            if (v == p)
                continue;
            if (!depth[v]) 
                dfs(v, u);
            else if (depth[v] < depth[u]) {
                // 发现反向边，说明找到了环
                int cu = u;
                while (cu != v) {
                    in_loop[cu] = true;
                    loop++;
                    cu = parent[cu];
                }
                in_loop[v] = true;
                loop++;
            }
        }
    }
    
    vector<int> bfs(int u, bool detect_loop) {
        // detect_loop为标志位，为true表示BFS的目标是找到环的入口
        // 如果detect_loop为false，表示BFS的目标是求出到所有点的最短距离
        vector<int> dist(n + 1, INF);
        queue<int> q;
        dist[u] = 0;
        q.push(u);
        while (!q.empty()) {
            int x = q.front();
            q.pop();
            if (detect_loop && in_loop[x])
                return {x, dist[x]};
            for (int y : adj[x]) {
                if (dist[y] <= dist[x] + 1)
                    continue;
                dist[y] = dist[x] + 1;
                q.push(y);
            }
        }
        return dist;
    }
public:
    int chaseGame(vector<vector<int>>& edges, int startA, int startB) {
        n = edges.size();
        adj = vector<vector<int>>(n + 1);
        for (auto v : edges) {
            adj[v[0]].emplace_back(v[1]);
            adj[v[1]].emplace_back(v[0]);
            // 如果两个人一开始就相邻，第一回合就能抓住
            if (v[0] == startA && v[1] == startB)
                return 1;
            if (v[0] == startB && v[1] == startA)
                return 1;
        }
        
        // DFS找环
        depth = vector<int>(n + 1);
        parent = vector<int>(n + 1);
        in_loop = vector<bool>(n + 1);
        dfs(1, 0);
        
        // BFS求出A和B到所有点的最短距离
        vector<int> da = bfs(startA, false);
        vector<int> db = bfs(startB, false);
        
        // 如果环的长度大于等于4，那么存在B永远无法被捉到的可能性
        if (loop >= 4) {
            // 寻找B到环的入口（可能就是B本身），及距离
            vector<int> qb = bfs(startB, true);
            // 如果A到B的入口的距离大于B到环的入口距离加一，则B可以永远不被捉到
            if (qb[1] + 1 < da[qb[0]])
                return -1;
        }
        
        // A一定可以捉到B，B要使自己尽可能晚被捉到
        int ans = 0;
        for (int i = 1; i <= n; ++i)
            // 如果一个点到A的最短距离大于到B的最短距离加一
            // 这个点就是B可以安全到达的点
            // 用它更新最后的结果
            if (da[i] > db[i] + 1)
                ans = max(ans, da[i]);
        return ans;
    }
};
 Comments
On this page
LCP 21-追逐游戏
  1. 解题思路
  2. 代码