LCP 23-魔术排列

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:32 2023-09-13 16:06:32 Updated    

秋日市集上，魔术师邀请小扣与他互动。魔术师的道具为分别写有数字 1~N 的 N 张卡牌，然后请小扣思考一个 N 张卡牌的排列 target。
魔术师的目标是找到一个数字 k（k >= 1），使得初始排列顺序为 1~N 的卡牌经过特殊的洗牌方式最终变成小扣所想的排列
target，特殊的洗牌方式为： - 第一步，魔术师将当前位于 偶数位置 的卡牌（下标自 1 开始），保持 当前排列顺序 放在位于
奇数位置 的卡牌之前。例如：将当前排列 [1,2,3,4,5] 位于偶数位置的 [2,4] 置于奇数位置的 [1,3,5] 前，排列变为
[2,4,1,3,5]； - 第二步，若当前卡牌数量小于等于 k，则魔术师按排列顺序取走全部卡牌；若当前卡牌数量大于 k，则取走前 k
张卡牌，剩余卡牌继续重复这两个步骤，直至所有卡牌全部被取走； 卡牌按照魔术师取走顺序构成的新排列为「魔术取数排列」，请返回是否存在这个数字 k
使得「魔术取数排列」恰好就是 target，从而让小扣感到大吃一惊。 示例 1： >输入：target = [2,4,3,1,5] >

输出：true > >解释：排列 target 长度为 5，初始排列为：1,2,3,4,5。我们选择 k = 2： >第一次：将当前排列
[1,2,3,4,5] 位于偶数位置的 [2,4] 置于奇数位置的 [1,3,5] 前，排列变为 [2,4,1,3,5]。取走前 2 张卡牌 2,4，剩余
[1,3,5]； >第二次：将当前排列 [1,3,5] 位于偶数位置的 [3] 置于奇数位置的 [1,5] 前，排列变为 [3,1,5]。取走前 2 张
3,1，剩余 [5]； >第三次：当前排列为 [5]，全部取出。 >最后，数字按照取出顺序构成的「魔术取数排列」2,4,3,1,5 恰好为 target。
示例 2： >输入：target = [5,4,3,2,1] > >输出：false > >解释：无法找到一个数字 k
可以使「魔术取数排列」恰好为 target。 提示： - 1 <= target.length = N <= 5000 - 题目保证
target 是 1~N 的一个排列。

比赛的时候思路出来了，可惜具体实现出了点问题，一直超时。

思路：

1、暴力法(超时)

题目给出了样例：
target = [2,4,3,1,5]
根据题目规则的第二步：

1
2
3
4
5
6
7
8
9
第一步，
魔术师将当前位于 偶数位置 的卡牌（下标自 1 开始），
保持 当前排列顺序 放在位于 奇数位置 的卡牌之前。
例如：将当前排列 [1,2,3,4,5] 位于偶数位置的 [2,4] 置于奇数位置的 [1,3,5] 前，
排列变为 [2,4,1,3,5]；

第二步，
若当前卡牌数量小于等于 k，则魔术师按排列顺序取走全部卡牌；
若当前卡牌数量大于 k，则取走前 k 张卡牌，剩余卡牌继续重复这两个步骤，直至所有卡牌全部被取走；

我们显然可以使用暴力法，**k的有效取值是从1到n**，当k大于n时，得到的效果其实和k==n是一样的。
所以我们直接把所有k的有效取值都按照题目的规则（洗牌、取牌）试一遍，肯定能找到答案。
但是这样显而易见超时了。

2、改进：充分利用第一次洗牌结果

超时之后我们就要思考如何优化k的取值。

这里依旧使用题目所给的target数组:
target:{2,4,3,1,5\

1、构造一个数组：
{1,2,3,4,5}

2、按照题目的规则排序，即把索引（从1开始）为偶数的放前面，得到第一次洗牌的结果（叫他firstSort数组吧）：
firstSort数组：{2,4,1,3,5\

3、然后我们把题目给的目标数组target从头开始进行比较。
firstSort数组：{\textcolor{red}{2,4}, 1,3,5
target数组: {\textcolor{red}{2,4},3,1,5\

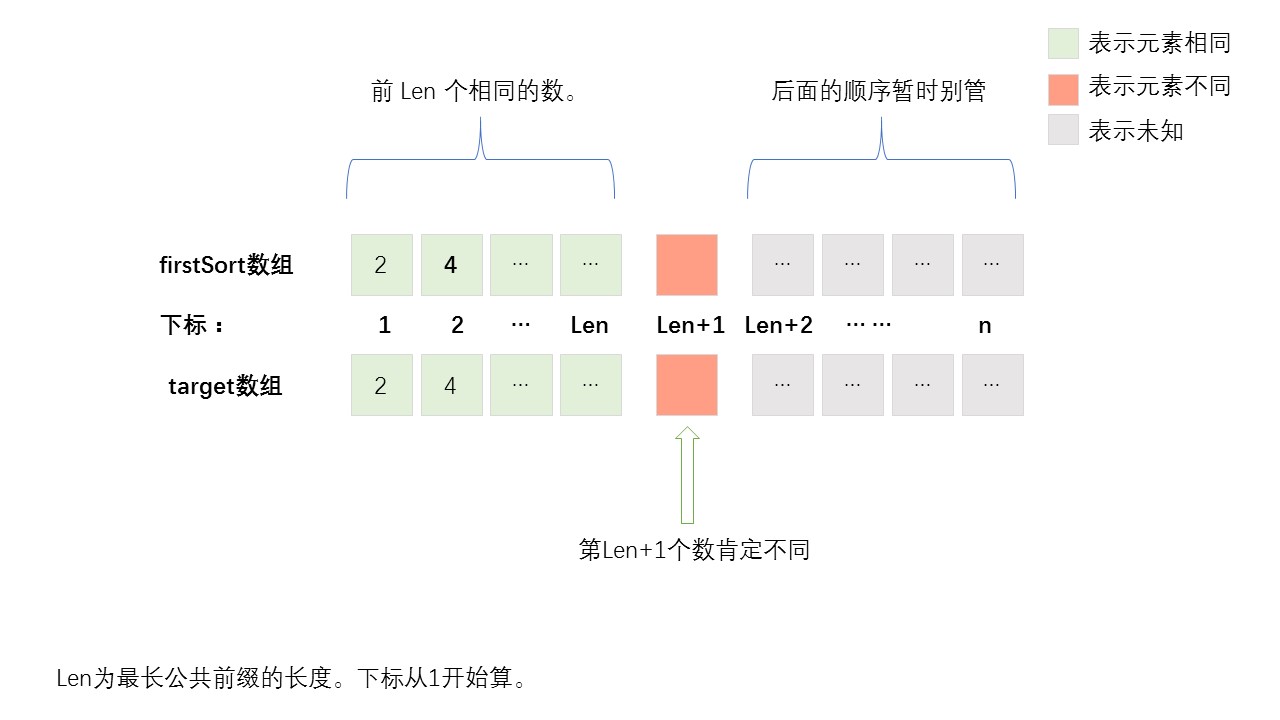
我们可以看到标红的2,4是两个数组最长公共前缀，设最长公共前缀的长度为Len。
这也就是说两个数组的前Len个数相同，第Len+1个数肯定不同。(除非两个数组完全相同，那就没有第Len+1个数了)

我们可以发现，k的取值是不能超过Len的：
因为如果k超过了Len，你第一次洗牌后取前k个数，其中前Len个数相同，第Len+1个数不同，那得到的结果肯定不同。

比如说在这个例子中，Len是等于2的，我取k等于3。那么第一次取出的k个数为:
{2,4,\textcolor{red}1
而target的前k个数为:
{2,4,\textcolor{red}3
很明显，后面不用继续取数，我们也知道结果不可能与target一样了。

那么k能不能小于Len呢？

答案是不能的。

我们简单地分析一下：

如图是第一次洗牌后的情况与target做对比。
幻灯片1.JPG

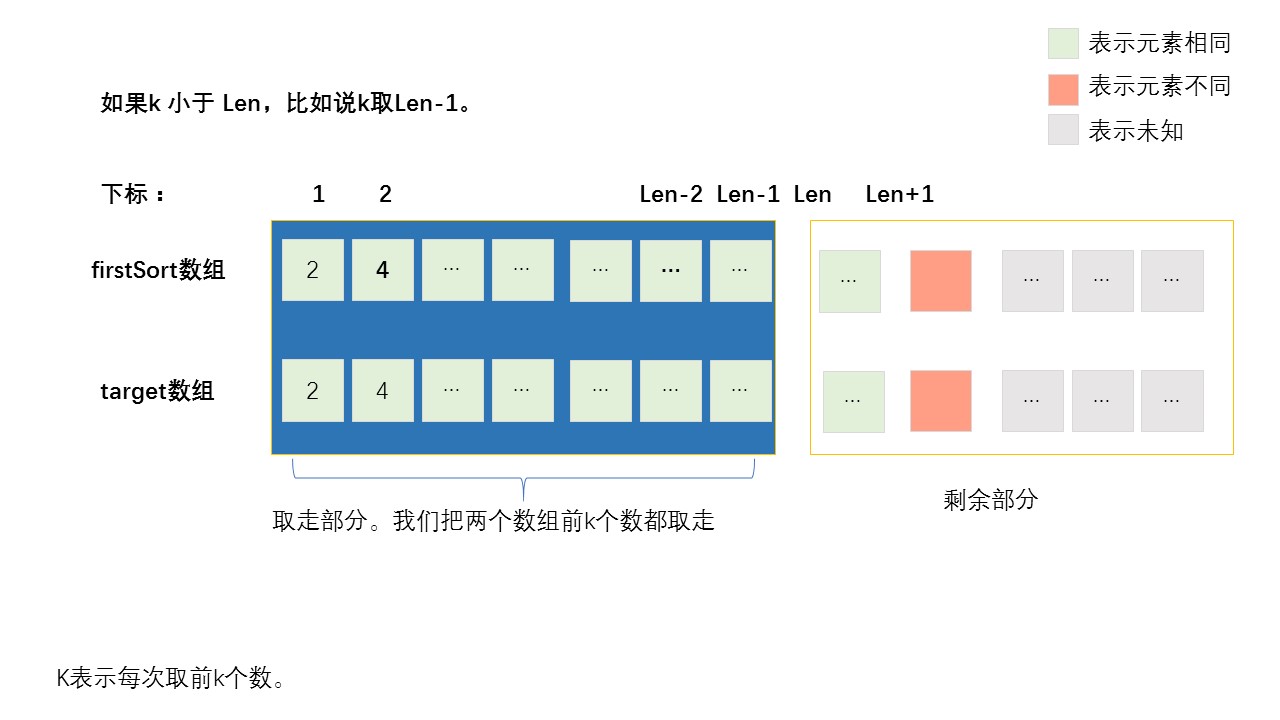
先假设 k=Len-1的情况，以简要分析。如图我们取出前Len-1个数，那么第Len个数就肯定被保留下来，参与下一轮洗牌。

幻灯片2.JPG



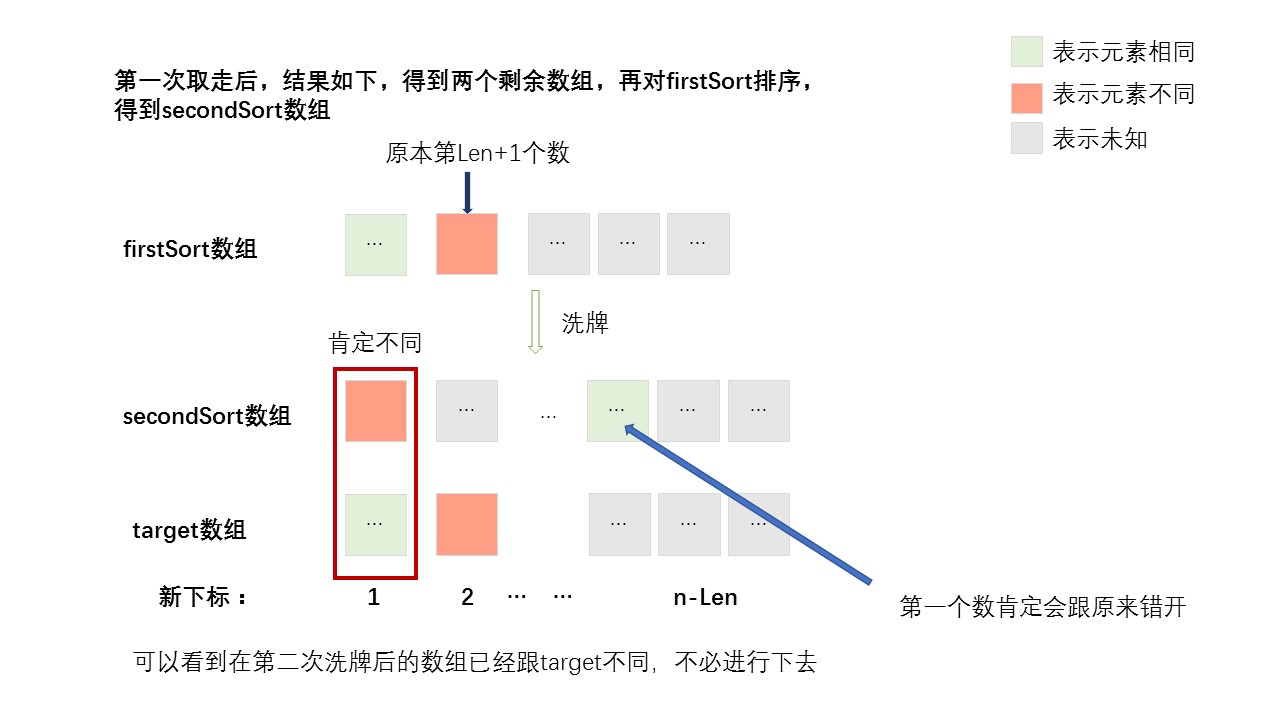
接下来，进行第二轮洗牌，如图所示，firstSort数组中的第一个数肯定会因为洗牌与target中相同的数错开（除非就剩一张牌，但是在第二轮洗牌中不可能只剩一张，因为这两个数组不可能前n-1个相同而最后一个数不同）。

因此，两个数组中的第一个数肯定不同。

并且，我们可以推广到k取Len-3 , Len-5 , Len-7 …一直到Len–num，其中num为表示任意奇数。
只要num为奇数，那么在新数组中的第1个数在洗牌后必然跟在target中的与他相同的数错开（看图容易理解）。

幻灯片3.JPG

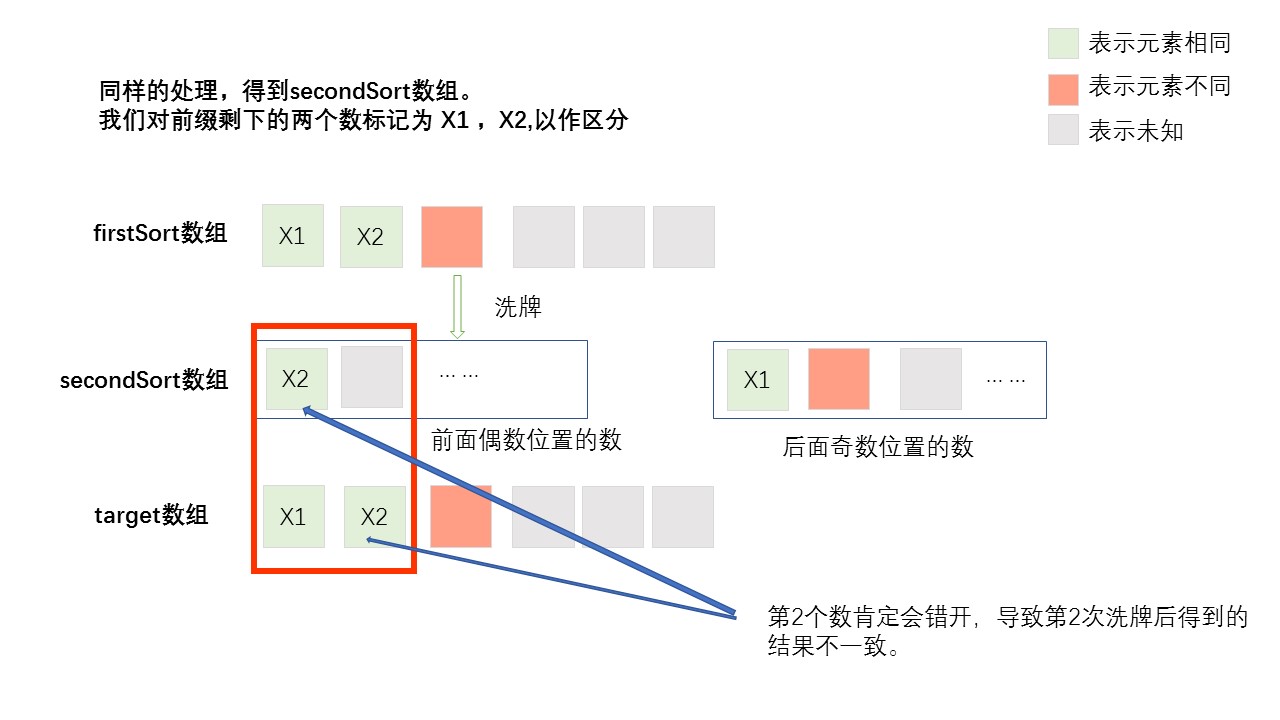
如果num为偶数的话，例如num=2，即k=Len-2，分析如下：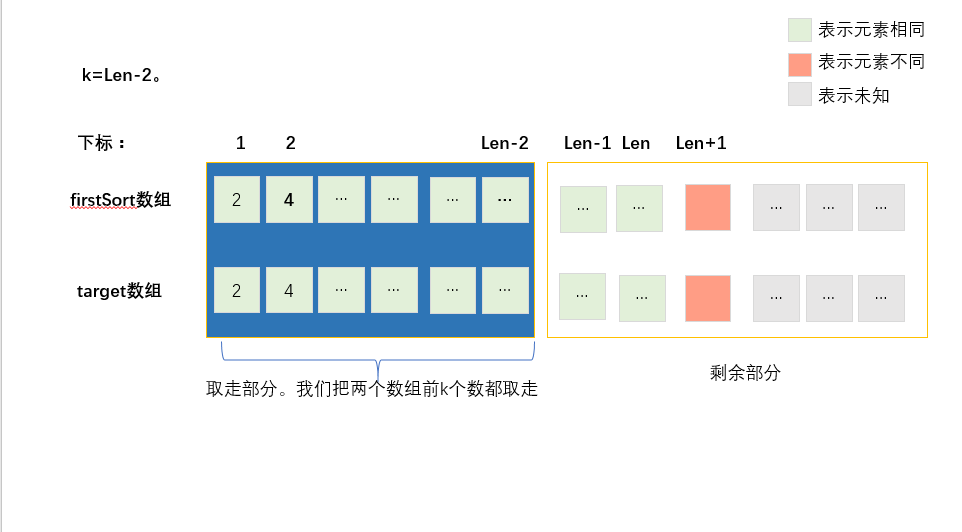
image.png

幻灯片4.JPG

经过上图简单的分析，显然num为2的时候剩余数组的第2个又会因为洗牌而错开，导致与结果不一致。

同样的道理可以推广到num=4，num=6...直到num为任意偶数。

所以到最后，我们发现只要对k==Len的情况进行模拟洗牌、取牌的过程，判断最后的结果是否与target相同就行。当然，如果中途发现不对，就可以提前退出

[]group
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
class Solution {
public:
    //题目的洗牌算法。可能大佬们有更好的写法
    void magicSort(vector<int>&nums)
    {
        vector<int>tmp=nums;
        int n=nums.size();
        int idx=0;
        for(int i=0;i<n;i++)
        {
            if((i+1)%2==0)
            {
                nums[idx++]=tmp[i];
                tmp[i]=-1;
            }
        }
        for(int i=0;i<n;i++)
        {
            if(tmp[i]==-1)continue;
            nums[idx++]=tmp[i];
        }
    }
    //获取第一次洗牌后的数组和target数组的公共最长前缀
    int getLen(vector<int>nums,vector<int>&target)
    {
        int n=nums.size();
        int Len=n;
        magicSort(nums);
        for(int i=0;i<n;i++)
        {
            if(nums[i]!=target[i])
            {
                Len=i;
                break;
            }
        }
        return Len;
    }
    bool isMagic(vector<int>& target) {
        if(target.size()==1)
        {
            return true;
        }

        int n=target.size();
        vector<int>nums(n);
        for(int i=0;i<n;i++)
        {
            nums[i]=i+1;   
        }
        int k=getLen(nums,target); 

        //公共前缀长度为0，那就不用看了
        if(k==0)
        {
            return false;
        }

        //洗牌最多有 n/k（向上取整）次
        int cnt=0;
        if(n%k==0)
        {
            cnt=n/k;
        }
        else cnt=n/k+1;


        int j=0;//j表示第几轮洗牌
        while(j<cnt)
        {
            magicSort(nums);
            
            bool flag=false;
            int size=nums.size();
            for(int i=0;i<k;i++)
            {
                if(i+k*j<n&&nums[i]!=target[i+k*j])
                {
                    flag=true;
                    break;
                }
            }

            //如果中途发现不对，就可以提前退出
            if(flag)
            {
                break;
            }
            else{
                
                //取走前k个
                for(int i=k;i<size;i++)
                {
                    nums[i-k]=nums[i];
                }
                if(size>k)
                {
                    nums.resize(size-k);
                }
                else{
                    nums.resize(0);
                }
                if(nums.size()==0)
                {
                    return true;
                }
            }
            j++;
        }   
        
        return false;
    }
};
[]group
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
class Solution {
    //洗牌过程
    int[] magicSort(int[] nums,int length)
    {
        int n=length;
        int result[]=new int[n];
        int mid=n/2;
        for(int i=0,even=0,odd=mid;i<n;i++)
        {
            if((i+1)%2==0)
            {
                result[even++]=nums[i];
            }
            else{
                result[odd++]=nums[i];
            }
        }
        return result;
    }

    int getLen(int[] firstSort,int[] target)
    {
        int n=firstSort.length;
        for(int i=0;i<n;i++)
        {
            if(firstSort[i]!=target[i])
            {
                return i;
            }
        }
        //两个数组完全相等，返回n
        return n;
    }

    public boolean isMagic(int[] target) {

        int n=target.length;
        int nums[]=new int[n];

        //构造数组:{1,2,3,4....n}
        Arrays.fill(nums,1);
        for(int i=1;i<n;i++)
        {
            nums[i]+=nums[i-1];
        }
        
        nums=magicSort(nums,nums.length);
        // System.out.println(Arrays.toString(nums));
        int k=getLen(nums,target);
        // System.out.println(k);

        if(k==0)
        {
            return false;
        }

        int numsLen=n;
        while(numsLen>0)
        {
            //取走前k个数
            for(int i=k;i<numsLen;i++)
            {
                nums[i-k]=nums[i];
                target[i-k]=target[i];
            }
            if(numsLen>k)
            {
                numsLen-=k;
            }
            else{
                numsLen=0;
            }
            if(numsLen==0)
            {
                return true;
            }
            nums=magicSort(nums,numsLen);
            for(int i=0;i<k&&i<numsLen;i++)
            {
                if(nums[i]!=target[i])
                {
                    return false;
                }
            }
        }
        return false; 
    }

}

代码写的难看了，没做过多优化，希望评论区大佬有更好的思路、写法补充。

码字不易，点个赞吧

 Comments
On this page
LCP 23-魔术排列
  1. 1、暴力法(超时)
  2. 2、改进：充分利用第一次洗牌结果