LCP 26-导航装置

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:23 2023-09-13 16:06:23 Updated    

小扣参加的秋日市集景区共有 N 个景点，景点编号为 1~N。景点内设有 N-1 条双向道路，使所有景点形成了一个二叉树结构，根结点记为
root，景点编号即为节点值。
由于秋日市集景区的结构特殊，游客很容易迷路，主办方决定在景区的若干个景点设置导航装置，按照所在景点编号升序排列后定义装置编号为 1 ~
M。导航装置向游客发送数据，数据内容为列表 [游客与装置 1 的相对距离,游客与装置 2 的相对距离,...,游客与装置 M 的相对距离]。由于游客根据导航装置发送的信息来确认位置，因此主办方需保证游客在每个景点接收的数据信息皆不相同。请返回主办方最少需要设置多少个导航装置。
示例 1： >输入：root = [1,2,null,3,4] > >输出：2 > >解释：在景点 1、3 或景点 1、4 或景点 3、4
设置导航装置。 > >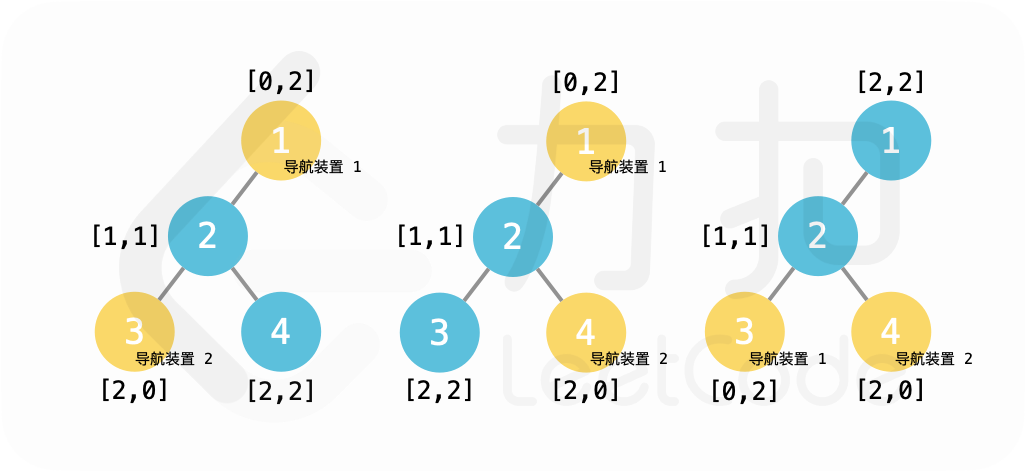![image.png](https://pic.leetcode-cn.com/1597996812-tqrgwu-
image.png){:height=”250px”} 示例 2： >输入：root = [1,2,3,4] > >输出：1 >

解释：在景点 3、4 设置导航装置皆可。 > >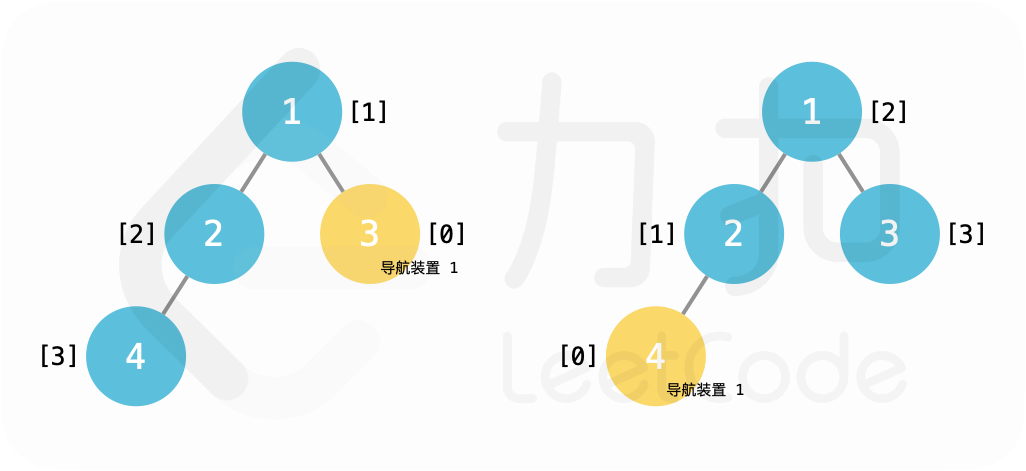![image.png](https://pic.leetcode-
cn.com/1597996826-EUQRyz-image.png){:height=”200px”} 提示： - 2 <= N <= 50000 - 二叉树的非空节点值为 1~N 的一个排列。

解题思路

算法思路

观察一个 “三叉节点”（既有父节点又有两个子节点的节点），如下图中的节点 1：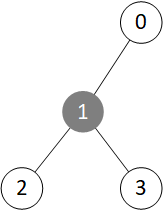
image.png
我们发现，如果只在节点 0 部署装置，则无法区分 2、3；如果在节点 2 部署装置，则无法区分 0、3；如果在节点 3 部署装置，则无法区分 0、2。（部署在节点 1 更不行，三个都区分不了）
也就是说，一个“三叉节点” 的 3 个 “子树” （把父节点也算上）中，至少有 2 个有导航装置。

有了这个结论，我们看看是否能用万能的 dfs 来解题。但很快就有一个问题，当 dfs 到某个节点时，我们并不知道其 父节点 那个子树是否有导航装置。

那么怎么办呢？可以 先假设父节点方向 有 导航装置，然后进行 dfs。

定义函数 dfs(node) 的返回值：节点 node 所在的子树中，是否 放置了 导航装置。dfs 时：

  • 如果一个节点是叶子节点（或者 null），则我们先暂时不放导航装置，返回 0。

  • 如果一个节点是“三叉节点”（拥有左、右两个子节点和父节点），且左、右两个子节点都 没有 导航装置（dfs 返回 0），那么我们 必须 在左右两个子树中，至少一个放置导航装置（至于放到哪个子树，我们不关心），答案 +1。然后函数返回 1，表明该节点的子树中，放置了导航装置。

  • 如果 dfs 时，发现 dfs(left) 或 dfs(right) 返回 1 时，则证明左子树或者右子树中，至少有 1 个有导航装置，那么再加上 父节点方向 的导航装置（根据假设），有两个够用了，于是不用增加答案。但是函数仍然返回 1，代表该节点的子树中，放置了导航装置。

我们还可以发现：

  • 如果一个节点 node（及其下方的子树）不是一条链（包含三叉节点），则 dfs(node) 一定返回 1；
  • 反之，dfs(node) 一定返回 0，并且 dfs(node) 不会增加答案。

好了，不要忘了我们之前假设 父节点方向 有导航装置。那么当 dfs 结束后，还需要重新检查一番。

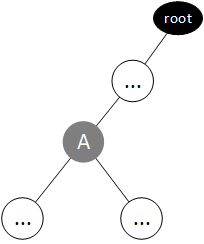
如果根节点是一个 “叶子” 节点（即只有 左/右 一棵子树），那么我们需要检测 离根节点最近的 三叉节点（下图中的节点 A）：

  • 如果该三叉节点 A 的左右两棵子树中，都包含导航装置，则节点 A 无需在父节点方向上增加导航装置。此外，节点 A 的左子树的节点的父节点方向（也就是外部）也有导航装置（在节点 A 的右子树中），右子树同理，故无需增加答案。
  • 否则，需要再在根节点上加一个导航装置。
    image.png

如果根节点有两棵子树，则分三种情况：

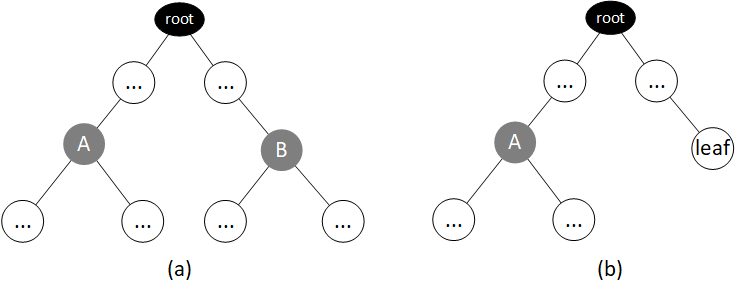
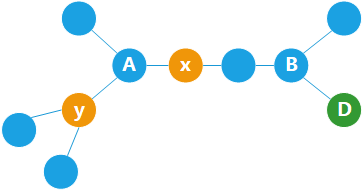
  • 如果根节点的两棵子树都包含三叉节点（此时 dfs(l) 和 dfs(r) 都会返回 1），如下图中的 (a) 情况，则节点 A 和 节点 B 下方的子树中都会放置导航装置，因此节点 A （及其子节点）的父节点方向有导航装置（在根节点的另一棵子树中）；节点 B 同理，因此无需增加答案。
  • 如果根节点的两棵子树之一包含三叉节点（此时 dfs(l) 和 dfs(r) 只有一个返回 1），另一棵子树是一条链，如下图中的 (b) 情况，我们注意到，这种情况和 “根节点只有 1 棵子树” 的情况并没有本质不同（因为节点 A 的父节点方向的形状都是一条链，都没有放导航装置），故判断逻辑也是一样的：判断距离根节点最近的三叉节点 A 的左右两棵子树中是否都有导航装置。
  • 如果根节点的两棵子树都是一条链（此时 dfs(l) 和 dfs(r) 都返回 0），则整棵树是一条链，因此总共需要 1 个导航装置；而此时因为 dfs(l) 和 dfs(r) 都不会增加答案，故最后也需要给答案 +1。
    image.png

代码中 变量 s 就记录了距根节点最近的三叉节点 是否 子树都含有导航装置。

s 的初值设为 1，因为如果树是一条链，则 s 的值不会改变，而这种情况最终答案还是要 +1 的。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int res = 0, s = 1;
    int dfs(TreeNode* root) {
        if(!root) {
            return 0;
        }
        int l = dfs(root->left), r = dfs(root->right);
        if(root->left && root->right) {
            res += !l && !r;
            s = !(l && r);
            return 1;
        }
        return l || r;
    }
    int navigation(TreeNode* root) {
        int l = dfs(root->left), r = dfs(root->right);
        return res + ((l && r)? 0 : s);
    }
};

时间、空间复杂度：O(N)。

想要证明的往下看

证明：如果树不是一条链，在最优化导航装置的位置的前提下，能够区分树中所有节点的 充分必要条件 是：所有三叉节点的 3 个子树中，至少有 2 个子树中有导航装置。
（如果树是一条链，则需要 1 个导航装置）

一、充分性。 我们任取两个节点。有 2 种可能的情况：

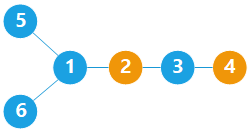
  1. 两个节点在同一路径上（这意味着两个节点之间没有三叉节点）， 举例如图所示，选取了节点 2 和节点 4。
    image.png
    三叉节点 1 至少有两个子树中有装置， 5 和 6 上至少有一个。而 5 或 6 上的装置都能区分节点 2 和 4。

  2. 如果两个节点不在同一条链上，那它们一定位于某一三叉节点的不同子树中。这样，其中一个节点所在的子树中一定含有导航装置。我们设这个节点为节点 x，另一个节点为节点 y，导航装置在节点 D 上。具体也分两种情况。
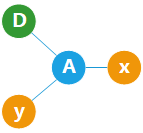
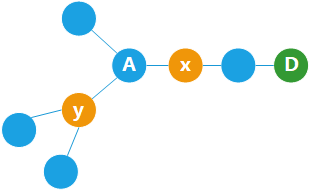
    情形一：节点 x 所在的子树是一条链，不包含三叉节点，如下图所示，节点 x 在三叉节点 A 的子树中。
    image.png
    此时，将导航装置 D 放在 x 所在叶子节点，则 D 与 x，y 的距离一定不同。
    情形二：节点 x 所在的子树不是一条链，意味着它还有子树，如下图所示。
    image.png
    此时，三叉节点 B 右侧的两个子树中至少有一个包含导航装置。而这个导航装置距离 x 一定比 y 更近。

  3. 综上所述，我们证明了：如果每个三叉节点的 3 个子树中，至少有 2 个中有装置，则存在一种方案，使任何两点都能够得到区分。

二、必要性。 如果某三叉节点只有 0 个或 1 个子树中包含导航装置，则一定存在两点不能被区分，如下图中的 x 和 y。
image.png

 Comments
On this page
LCP 26-导航装置
  1. 解题思路