LCP 27-黑盒光线反射

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:28 2023-09-13 16:06:28 Updated    

秋日市集上有个奇怪的黑盒，黑盒的主视图为 n\m 的矩形。从黑盒的主视图来看，黑盒的上面和下面各均匀分布有 m 个小孔，黑盒的左面和右面各均匀分布有 n
个小孔。黑盒左上角小孔序号为 0，按顺时针编号，总共有 2(m+n)
个小孔。每个小孔均可以打开或者关闭，初始时，所有小孔均处于关闭状态。每个小孔上的盖子均为镜面材质。例如一个 2\*3 的黑盒主视图与其小孔分布如图所示:
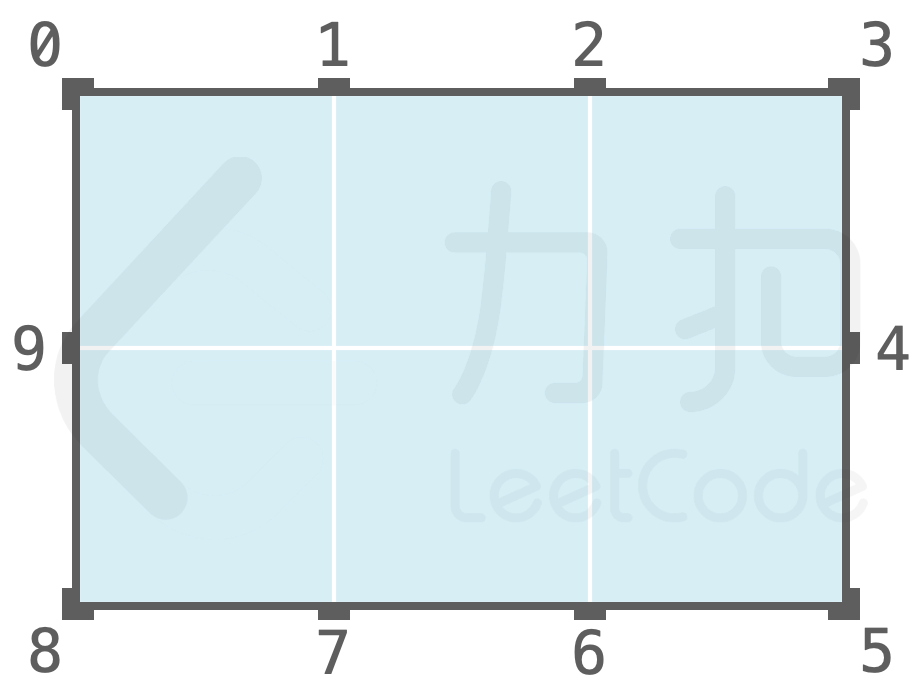![image.png](https://pic.leetcode-cn.com/1598951281-ZCBrif-
image.png){:height=”200px”} 店长告诉小扣，这里是「几何学的快问快答」，店长可能有两种操作： - open(int index, int direction) - 若小孔处于关闭状态，则打开小孔，照入光线；否则直接照入光线； - close(int index)

  • 关闭处于打开状态小孔，店长保证不会关闭已处于关闭状态的小孔； 其中： - index： 表示小孔序号 - direction：1
    表示光线沿 y=x 方向，-1 表示光线沿 y=-x 方向。 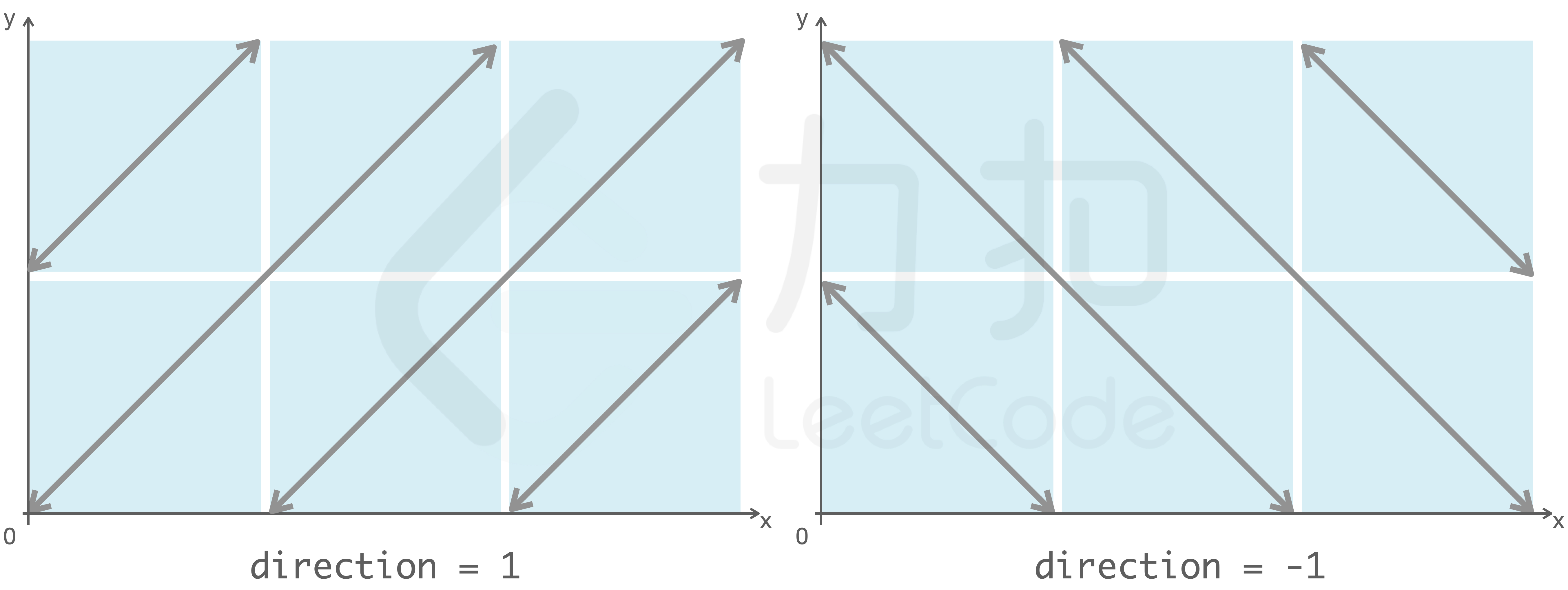![image.png](https://pic.leetcode-
    cn.com/1599620810-HdOlMi-image.png){:height=”200px”}
    当光线照至边界时：若边界上的小孔为开启状态，则光线会射出；否则，光线会在小孔之间进行反射。特别地： 1.
    若光线射向未打开的拐角（黑盒顶点），则光线会原路反射回去； 2. 光线自拐角处的小孔照入时，只有一种入射方向（如自序号为 0 的小孔照入方向只能为
    -1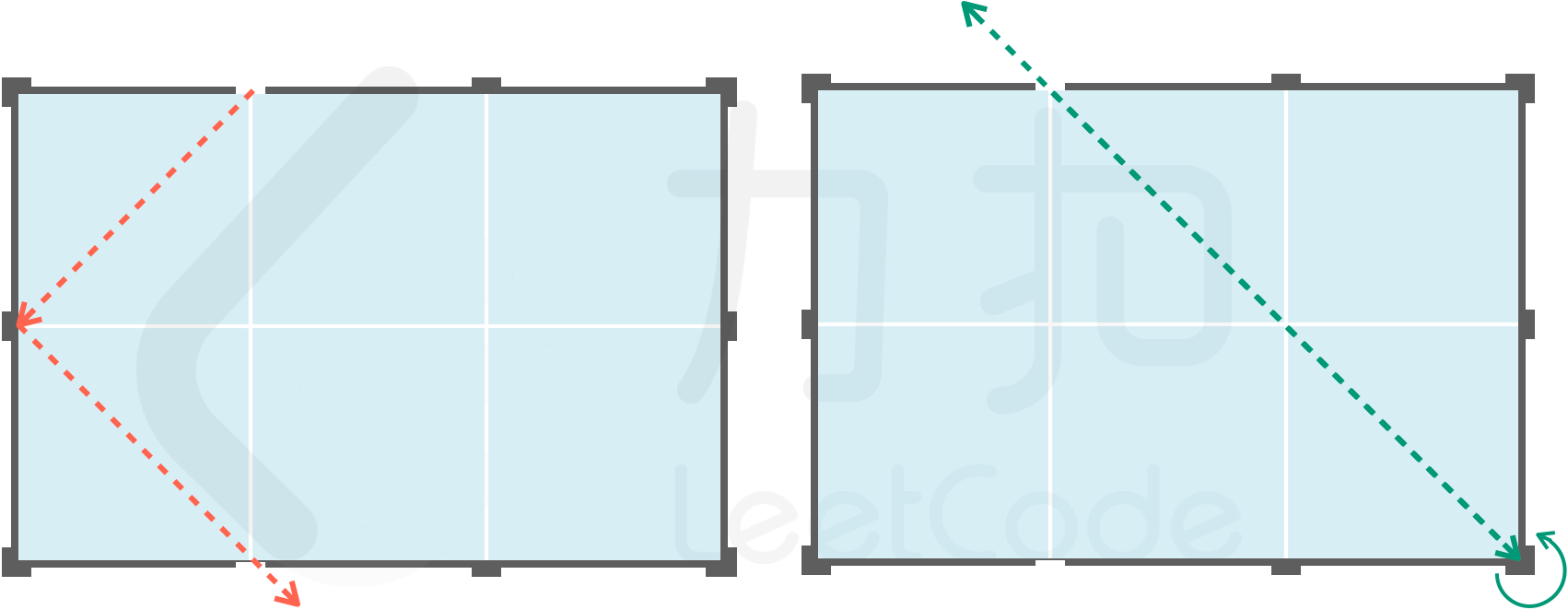） ![image.png](https://pic.leetcode-cn.com/1598953840-DLiAsf-
    image.png){:height=”200px”} 请帮助小扣判断并返回店长每次照入的光线从几号小孔射出。 示例 1： >输入：

    ["BlackBox","open","open","open","close","open"]
    [[2,3],[6,-1],[4,-1],[0,-1],[6],[0,-1]] > >输出：[null,6,4,6,null,4] > >解释：
    BlackBox b = BlackBox(2,3); // 新建一个 2x3 的黑盒 >b.open(6,-1) // 打开 6 号小孔，并沿 y=-x
    方向照入光线，光线至 0 号小孔反射，从 6 号小孔射出 >b.open(4,-1) // 打开 4 号小孔，并沿 y=-x 方向照入光线，光线轨迹为
    4-2-8-2-4，从 4 号小孔射出 >b.open(0,-1) // 打开 0 号小孔，并沿 y=-x 方向照入光线，由于 6 号小孔为开启状态，光线从
    6 号小孔射出 >b.close(6) // 关闭 6 号小孔 >b.shoot(0,-1) // 从 0 号小孔沿 y=-x 方向照入光线，由于 6
    号小孔为关闭状态，4 号小孔为开启状态，光线轨迹为 0-6-4，从 4 号小孔射出 示例 2： >输入：
    ["BlackBox","open","open","open","open","close","open","close","open"]
    [[3,3],[1,-1],[5,1],[11,-1],[11,1],[1],[11,1],[5],[11,-1]] >
    输出：[null,1,1,5,1,null,5,null,11] > >解释： >
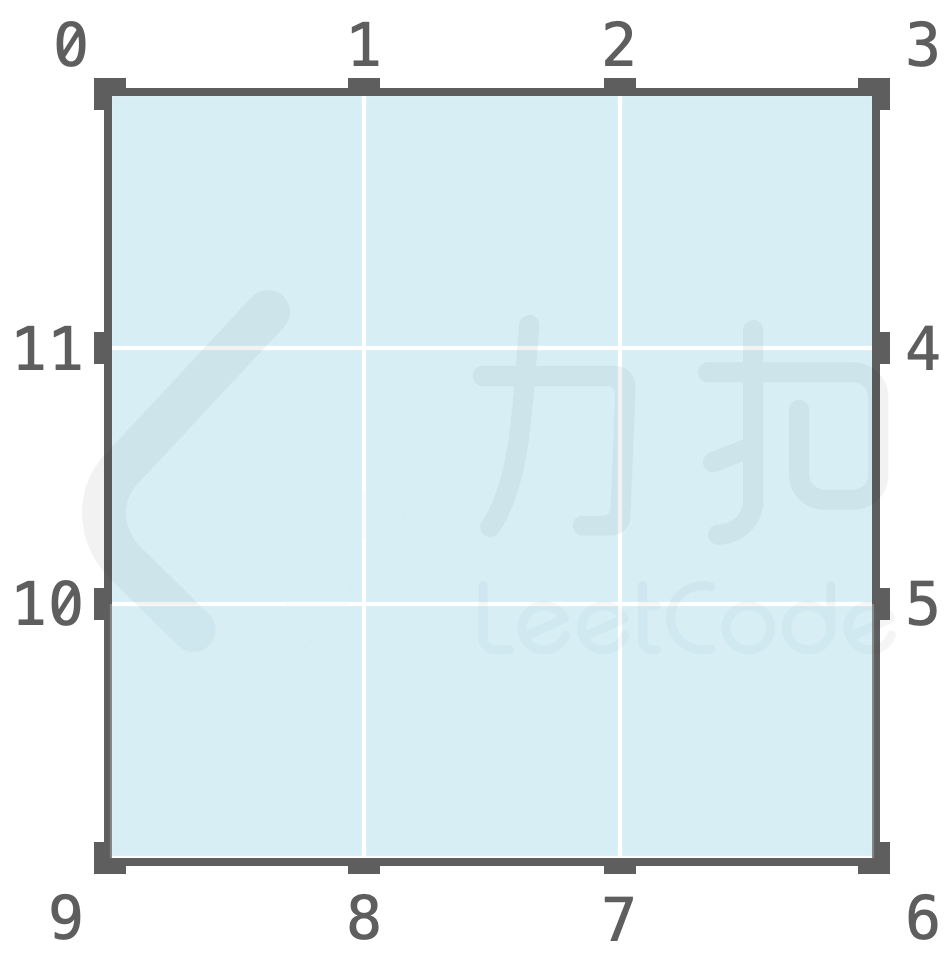    ![image.png](https://pic.leetcode-cn.com/1599204202-yGDMVk-
    image.png){:height=”300px”} > >BlackBox b = BlackBox(3,3); // 新建一个 3x3 的黑盒
    b.open(1,-1) // 打开 1 号小孔，并沿 y=-x 方向照入光线，光线轨迹为 1-5-7-11-1，从 1 号小孔射出
    b.open(5,1) // 打开 5 号小孔，并沿 y=x 方向照入光线，光线轨迹为 5-7-11-1，从 1 号小孔射出 >b.open(11,-1)
    // 打开 11 号小孔，并沿逆 y=-x 方向照入光线，光线轨迹为 11-7-5，从 5 号小孔射出 >b.open(11,1) // 从 11 号小孔沿
    y=x 方向照入光线，光线轨迹为 11-1，从 1 号小孔射出 >b.close(1) // 关闭 1 号小孔 >b.open(11,1) // 从 11
    号小孔沿 y=x 方向照入光线，光线轨迹为 11-1-5，从 5 号小孔射出 >b.close(5) // 关闭 5 号小孔 >b.open(11,-1)
    // 从 11 号小孔沿 y=-x 方向照入光线，光线轨迹为 11-1-5-7-11，从 11 号小孔射出 提示： - 1 <= n, m <= 10000 - 1 <= 操作次数 <= 10000 - direction 仅为 1 或 -1 - 0 <= index < 2*(m+n)

感谢 @anhpp-i 指出两处 typo，已修改～

思路

在任意时刻，光的状态一定为 4(m+n)-4 种状态之一，即：

  • 从某个小孔沿着 y=x 方向射出；
  • 从某个小孔沿着 y=-x 方向射出。

由于有 2(m+n) 个小孔，并且角上的 4 个小孔只有一个方向可以射出，因此状态数为 2 \times 2(m+n)-4 = 4(m+n)-4。

对题目进行严（da）谨（dan）分（cai）析（xiang），可以得出一个非常有用的结论：

如果所有小孔都是关闭的状态，并且我们从第 i 号小孔以 d 方向射出光线，那么最终光线会重新射入第 i 号小孔，并且以 d 方向重新射出。也就是说，光线陷入了一个无尽的「循环」。

证明这个结论也很简单。首先，由于状态数是有限的，那么光线如果第二次到达某一个状态，那么它就陷入了循环，我们只需要证明最先到达第二次的那个状态就是「从第 i 号小孔以 d 方向射出光线」这个状态就行了。假设我们最先到达第二次的状态 X 不是光线初始的射出状态，那么我们可以「逆推」光线的路径，那么从这个状态一定可以「逆推」到初始状态：也就是从光线初始的射出状态到第一次出现状态 X 的这条路径，在到达第二次出现状态 X 之前也经过了一遍，因此初始的射出状态一定已经到达过第二次了。

因此，我们可以把这些循环全部预处理出来。假设某一个循环是：

X_0, X_1, X_2, \cdots, X_{i-1}, X_i, X_{i+1}, \cdots, X_u

其中每一个 X 都是一种状态，并且状态 X_u 的下一种状态就是 X_0（即循环），那么如果光线从 X_i 开始，那么它会射出的小孔为：

  • 如果 X_{i+1}, \cdots, X_u 中有打开的小孔，那么射出的小孔就是其中打开的且编号最小的状态对应的小孔；
  • 如果没有，那么射出的小孔就是 X_0, \cdots, X_i 中打开的且编号最小的状态对应的小孔。由于 X_i 对应的小孔是打开的，因此我们一定可以找到答案。

如何通过上面的方法找出编号最小的小孔呢？我们可以想到使用有序集合（即 C++ 中的 std::set，Java 中的 TreeSet，很可惜 Python 中没有）。在有序集合中，我们可以查询严格大于某个给定元素的最小的元素，那么：

  • 我们首先查询是否有编号严格大于 t 的状态，如果有，会返回编号最小的那个状态；
  • 如果没有，我们只需要返回集合中编号最小的状态即可。

上述查询的时间复杂度为 \log N，其中 N 是集合中的元素个数。因此我们就可以这样做：

  • 我们首先预处理出所有的循环，显然每一个状态在所有的循环中恰好只出现一次，但每个小孔在所有的循环中最多出现两次（如果在角上，那么出现一次，否则出现两次）；

  • 每一个循环对应一个有序集合；

  • 当我们遇到 open(index, direction) 操作时：

    • 我们将 index 所在的循环的有序集合中插入 location(index), index 这个二元组，其中 location(index) 表示 index 在循环中的编号。注意 index 可能对应一或两个循环，我们需要插入一或两个二元组；
    • 随后我们找到 index, direction 唯一对应的状态以及包含这一状态的有序集合，进行上文提到的查询操作，得到答案。

  • 当我们遇到 close(index) 操作时：

    • 我们将 index 所在的循环的有序集合中删除 location(index), index 这个二元组，同样可能需要删除一或两个二元组。

由于我们使用的全部是二元组，因此可以考虑直接使用有序映射（即 C++ 中的 std::map，Java 中的 TreeMap，同样 Python 中没有）。

细节

最后一个问题就是，如何找出所有的循环呢？我们可以用横竖坐标来进行光线的路线模拟，但这里有非常好用的办法：

  • 如果当前的方向是 y=x，那么从第 i 个小孔射出，会到达第 2(m+n)-i 个小孔；
  • 如果当前的方向是 y=-x，那么从第 i 个小孔射出，并且小孔在「经过左上角的 y=-x 的直线」的右侧（即 i \leq 2m），那么会到达第 2m-i 个小孔，否则会到达第 2(2m+n)-i 个小孔。

同样我们可以确定光线的方向：

  • 经过一个小孔后，方向会变化，即从 y=x 变成 y=-x 或反之，但如果是经过角上的小孔，按么方向不会变化。

读者可以在草稿纸上画一画得到这些结论。这样我们既可以很方便地预处理出所有循环了。

代码

读者可以根据代码中的注释理解代码。时间复杂度为预处理 O(m+n) 以及单次 open()/close() 操作 O(\log(m+n))。


[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
class BlackBox {
private:
    // 存储从每个小孔以 y=x 方向射出时，所在的循环的 id 以及在循环中的 id
    vector<pair<int, int>> groupPos;
    // 存储从每个小孔以 y=-x 方向射出时，所在的循环的 id 以及在循环中的 id
    vector<pair<int, int>> groupNeg;
    // 存储每个循环的有序映射
    vector<map<int, int>> groupStats;

public:
    BlackBox(int n, int m) {
        int ptCount = (n + m) * 2;
        groupPos.assign(ptCount, {-1, -1});
        groupNeg.assign(ptCount, {-1, -1});
        for (int i = 0; i < ptCount; ++i) {
            // 如果不是左上角或者右下角的小孔，那么从 y=x 方向射出找循环
            if (i != 0 && i != m + n && groupPos[i].first == -1) {
                createGroup(n, m, i, 1);
            }
            // 如果不是左下角或者右上角的小孔，那么从 y=-x 方向射出找循环
            if (i != m && i != m * 2 + n && groupNeg[i].first == -1) {
                createGroup(n, m, i, -1);
            }
        }
    }

    void createGroup(int n, int m, int index, int direction) {
        int groupId = groupStats.size();
        int groupLoc = 0;
        groupStats.emplace_back();
        // 不断模拟光线的路径，直到走到一个已经遇见过的状态，这样就找到了一个循环
        while (!(direction == 1 && groupPos[index].first != -1) && !(direction == -1 && groupNeg[index].first != -1)) {
            if (direction == 1) {
                groupPos[index] = {groupId, groupLoc++};
                index = (n + m) * 2 - index;
            }
            else {
                groupNeg[index] = {groupId, groupLoc++};
                if (index <= m * 2) {
                    index = m * 2 - index;
                }
                else {
                    index = (m * 2 + n) * 2 - index;
                }
            }
            // 如果小孔不在角上，就改变方向
            if (index != 0 && index != m && index != m + n && index != m * 2 + n) {
                direction = -direction;
            }
        }
    }
    
    int open(int index, int direction) {
        // 插入二元组
        if (auto [groupId, groupLoc] = groupPos[index]; groupId != -1) {
            groupStats[groupId].emplace(groupLoc, index);
        }
        if (auto [groupId, groupLoc] = groupNeg[index]; groupId != -1) {
            groupStats[groupId].emplace(groupLoc, index);
        }

        // 查询
        auto [groupId, groupLoc] = (direction == 1 ? groupPos[index] : groupNeg[index]);
        auto& store = groupStats[groupId];
        if (auto iter = store.upper_bound(groupLoc); iter != store.end()) {
            return iter->second;
        }
        else {
            return store.begin()->second;
        }
    }
    
    void close(int index) {
        // 删除二元组
        if (auto [groupId, groupLoc] = groupPos[index]; groupId != -1) {
            groupStats[groupId].erase(groupLoc);
        }
        if (auto [groupId, groupLoc] = groupNeg[index]; groupId != -1) {
            groupStats[groupId].erase(groupLoc);
        }
    }
};
 Comments
On this page
LCP 27-黑盒光线反射