LCP 34-二叉树染色

小扣有一个根结点为 root 的二叉树模型，初始所有结点均为白色，可以用蓝色染料给模型结点染色，模型的每个结点有一个 val
价值。小扣出于美观考虑，希望最后二叉树上每个蓝色相连部分的结点个数不能超过 k 个，求所有染成蓝色的结点价值总和最大是多少？ 示例 1： >
输入：root = [5,2,3,4], k = 2 > > 输出：12 > > 解释：结点 5、3、4 染成蓝色，获得最大的价值 5+3+4=12 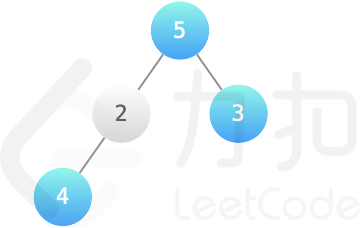![image.png](https://pic.leetcode-cn.com/1616126267-BqaCRj-
image.png) 示例 2： > 输入：root = [4,1,3,9,null,null,2], k = 2 > > 输出：16 >

解释：结点 4、3、9 染成蓝色，获得最大的价值 4+3+9=16 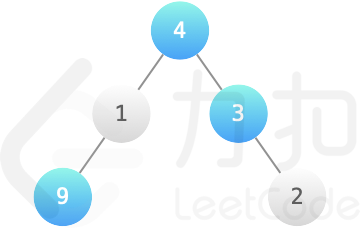![image.png](https://pic.leetcode-
cn.com/1616126301-gJbhba-image.png) 提示： + 1 <= k <= 10 + 1 <= val <= 10000 + 1 <= 结点数量 <= 10000

状态定义

f[i], (0≤i≤k) 表示以该节点为根，相邻的子节点为蓝色的个数为 i 的情况下（包括自身），节点价值总和的最大值；

状态计算

当 i = 0 时，即表示当前节点为白色，此时无所谓相邻子节点什么颜色，所以当前节点为根价值总和的最大值为左子节点所有情况和右子节点所有情况的最大值，即 f[0] = max(f_l) + max(f_r)；
当 i = 1 时，即表示当前节点为蓝色，且除自身外相邻的子节点为蓝色的个数为 0，所以当前节点为根价值总和的最大值为左子节点为白色和右子节点为白色的最大值加上自身的值，即 f[1]=root.val+f_l[0]+f_r[0]；
当 i = 2 时，即表示当前节点为蓝色，且除自身外相邻的子节点为蓝色的个数为 1，所以当前节点为根价值总和的最大值可分多种情况，即蓝色节点在左边和在右边的情况；
- 例如，k=2 时，可分为左边 1 个右边 0 个，和左边 0 个右边 1 个两种情况，即 f[2]=max(root.val+f_l[0]+f_r[1]，root.val+f_l[1]+f_r[0]);
- 例如，k=3 时，(除去自身算 1 个）可分为左 0 右 2 、左 1 右 1、左 2 右 0 三种情况；

故，
f[0]=max(f_l) + max(f_r)，i=0\f[i]=max(val+f_l[j]+f_r[i-j-1])，0<i≤k,0<j<i

初始状态

当前节点为空时，f[i]=0，0≤i≤k；

最终结果

根节点所有情况的最大值，max(f)；

[1]class Solution {
    vector<int> dfs(TreeNode* root, int k) {
        vector<int> f(k + 1, 0);
        if (!root) return f;
        auto l = dfs(root->left, k);
        auto r = dfs(root->right, k);
        f[0] = *max_element(l.begin(), l.end()) + *max_element(r.begin(), r.end());
        for (int i = 1; i <= k; ++i) {
            for (int j = 0; j < i; ++j) {
                f[i] = max(f[i], root->val + l[j] + r[i - j - 1]);
            }
        }
        return f;
    }
public:
    int maxValue(TreeNode* root, int k) {
        auto f = dfs(root, k);
        return *max_element(f.begin(), f.end());
    }
};

[1]/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */
var maxValue = function(root, k) {
    const dfs = (root, k) => {
        const f = new Array(k + 1).fill(0)
        if (!root) {
            return f
        }
        const l = dfs(root.left, k)
        const r = dfs(root.right, k)
        f[0] = Math.max(...l) + Math.max(...r)
        for (let i = 1; i <= k; ++i) {
            for (let j = 0; j < i; ++j) {
                f[i] = Math.max(f[i], root.val + l[j] + r[i - j - 1])
            }
        }
        return f
    }
    return Math.max(...dfs(root, k))
};

复杂度分析

时间复杂度 \mathcal O(k^2n);
空间复杂度 \mathcal O(kn)（未计算空节点的情况）。