二维平面上有 N 条直线，形式为 y = kx + b，其中 k、b为整数且 k > 0。所有直线以 [k,b]
的形式存于二维数组 lines 中，不存在重合的两条直线。两两直线之间可能存在一个交点，最多会有 C_N^2
个交点。我们用一个平行于坐标轴的矩形覆盖所有的交点，请问这个矩形最小面积是多少。若直线之间无交点、仅有一个交点或所有交点均在同一条平行坐标轴的直线上，则返回0。
注意：返回结果是浮点数，与标准答案 绝对误差或相对误差 在 10^-4 以内的结果都被视为正确结果 示例 1： > 输入：lines = [[2,3],[3,0],[4,1]] > > 输出：48.00000 > > 解释：三条直线的三个交点为 (3, 9) (1, 5) 和 (-1,
-3)。最小覆盖矩形左下角为 (-1, -3) 右上角为 (3,9)，面积为 48 示例 2： > 输入：lines = [[1,1],[2,3]] > > 输出：0.00000 > > 解释：仅有一个交点 (-2，-1） 限制： + 1 <= lines.length <= 10^5 且 lines[i].length == 2 + 1 <= lines[0] <= 10000 +
-10000 <= lines[1] <= 10000 + 与标准答案绝对误差或相对误差在 10^-4 以内的结果都被视为正确结果

解题思路

~~翻了翻比赛的时候大家的代码，感觉都好长。我虽然写了好几行废话，但感觉还是挺短的！~~

首先，我们可以把问题看成是求所有交点 x 和 y 的最大最小值。那第一反应就是联立方程求交点，得到：x = -b_i - b_j}{k_i - k_j。但其实正负不重要，反正我们需要的是最大值和最小值的差。同理，y 只需要把 k_i 换成 1}{k_i 就可以了，下面我们都以 x 为例讨论。

这样，问题变成了在 k-b 平面上有 n 个点，我们要求斜率最大和最小的一条线段。当然，正无穷的斜率是不合法的，因为平行线并不会相交。

然后，通过我们仔细的观察，只有下图红线所示的这类线段才可能成为最终的答案。即按照 k 分类排序后，只有相邻两列的最上、最下两个顶点之间的连线才有可能构成答案。这个可以分下面两步来证明：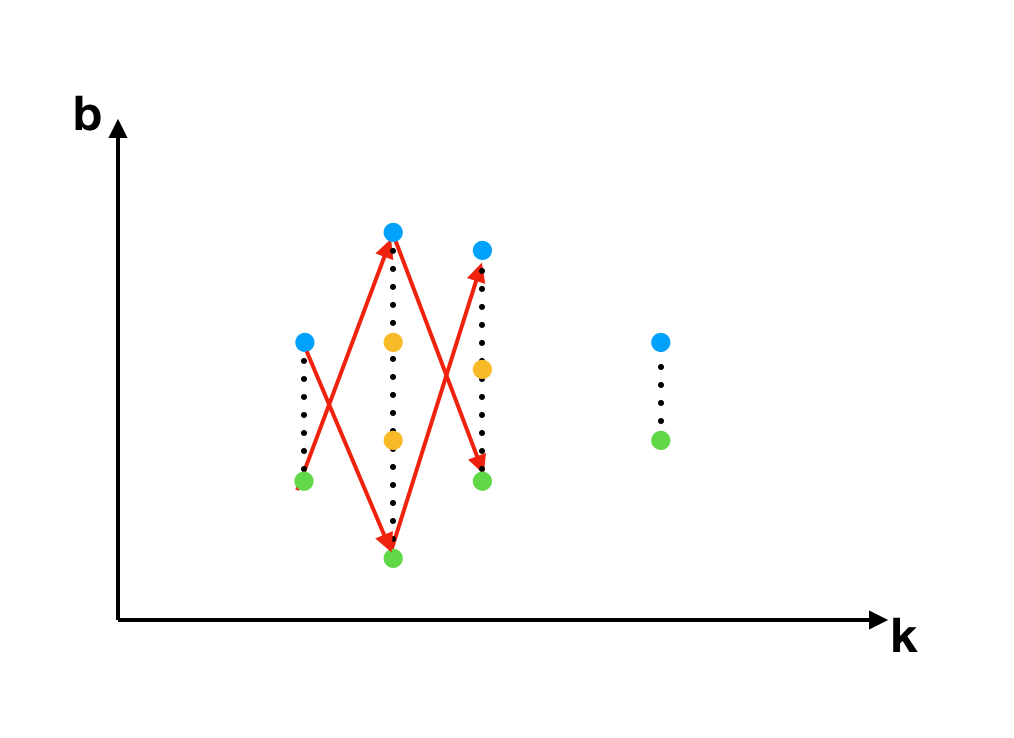

答案一定出现在相邻两列中。这个可以反证，如果答案出现在不相同的两列中，例如下图中的 A 和 C 两个点。对于中间某一列上的任意一个点 B，显然 AB 和 BC 的斜率一定是一个大于等于 AC, 一个小于等于 AC，且仅在 ABC 三点共线时等号成立。所以 AC 一定不可能构成答案。
相邻两列中一定是上下两端的节点构成答案，这个很显然。

综上，我们得到了一个做法，只需要按照 (k, b) 将所有点排序，维护三个 pointer 表示相邻两段，就可以快速得到答案。整体的复杂度是 O(nlogn)。

代码

class Solution {
public:
    double minRecSize(vector<vector<int>>& f) {
        int n = f.size();
        vector<int> k(n, 0), b(n, 0);
        sort(f.begin(), f.end());
        for (int i = 0; i < n; i++) {
            k[i] = f[i][0]; b[i] = f[i][1];
        }
        int p = 0, q = 0;
        while (q < n && k[q] == k[p]) q++;
        if (q >= n) return 0.;
        double x_min = 1e100, x_max = -1e100;
        double y_min = 1e100, y_max = -1e100;
        for (; q < n;) {
            int r = q;
            while (r + 1 < n && k[r + 1] == k[q]) r++;
            // [p, q - 1], [q, r]
            double cx1 = 1.0 * (b[r] - b[p]) / (k[r] - k[p]);
            double cx2 = 1.0 * (b[q] - b[q - 1]) / (k[q] - k[q - 1]);
            x_min = min(x_min, min(cx1, cx2));
            x_max = max(x_max, max(cx1, cx2));
            double cy1 = 1.0 * (b[r] * k[p] - b[p] * k[r]) / (k[r] - k[p]);
            double cy2 = 1.0 * (b[q] * k[q - 1] - b[q - 1] * k[q]) / (k[q] - k[q - 1]);
            y_min = min(y_min, min(cy1, cy2));
            y_max = max(y_max, max(cy1, cy2));
            p = q;
            while (q < n && k[q] == k[p]) q++;
        }
        return (x_max - x_min) * (y_max - y_min);
    }
};

LCP 37-最小矩形面积

解题思路

代码