LCP 38-守卫城堡

城堡守卫游戏的胜利条件为使恶魔无法从出生点到达城堡。游戏地图可视作 2*N 的方格图，记作字符串数组 grid，其中： - "."
表示恶魔可随意通行的平地； - "#" 表示恶魔不可通过的障碍物，玩家可通过在 平地 上设置障碍物，即将 "." 变为 "#"
以阻挡恶魔前进； - "S" 表示恶魔出生点，将有大量的恶魔该点生成，恶魔可向上/向下/向左/向右移动，且无法移动至地图外； - "P"
表示瞬移点，移动到 "P" 点的恶魔可被传送至任意一个 "P" 点，也可选择不传送； - "C" 表示城堡。
然而在游戏中用于建造障碍物的金钱是有限的，请返回玩家最少需要放置几个障碍物才能获得胜利。若无论怎样放置障碍物均无法获胜，请返回 -1。 注意：
- 地图上可能有一个或多个出生点 - 地图上有且只有一个城堡 示例 1 >输入：grid = ["S.C.P#P.", ".....#.S"] > >输出：3 > >解释：至少需要放置三个障碍物 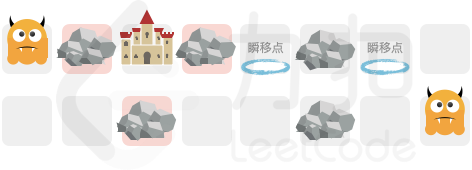![image.png](https://pic.leetcode-
cn.com/1614828255-uuNdNJ-image.png) 示例 2： >输入：grid = ["SP#P..P#PC#.S", "..#P..P####.#"] > >输出：-1 > >解释：无论怎样修筑障碍物，均无法阻挡最左侧出生的恶魔到达城堡位置
示例
3： >输入：grid = ["SP#.C.#PS", "P.#...#.P"] > >输出：0 > >解释：无需放置障碍物即可获得胜利
示例
4： >输入：grid = ["CP.#.P.", "...S..S"] > >输出：4 > >解释：至少需要放置 4
个障碍物，示意图为放置方法之一 ![image.png](https://pic.leetcode-cn.com/1614828218-sIAYkb-
image.png) 提示： - grid.length == 2 - 2 <= grid[0].length == grid[1].length <= 10^4 - grid[i][j] 仅包含字符 "."、"#"、"C"、"P"、"S"

前言

由于本题是「力扣杯」的竞赛题，因此只会给出提示、简要思路以及代码，不会对算法本身进行详细说明，希望读者多多思考。

方法一：拆点 + 最小割

提示 1

我们希望「恶魔」无法到达城堡，即「城堡」和「恶魔」之间不连通，对应到图论模型上就是「割」问题。

思路

使用最小割建模：

• 将每一个非「障碍物」的格子拆分成两个点，一个作为「起点」一个作为「终点」。
  • 如果该格子是「空地」，连接一条流量为 1 的边。
  • 否则，连接一条流量为 \infty 的边。
• 相邻两个格子之间，从一个格子的「终点」到另一个格子的「起点」连接一条流量为 \infty 的边。
• 对于所有「传送门」，它们的「终点」向「超级传送门节点」连接一条流量为 \infty 的边，并从该节点连回「起点」一条流量为 \infty 的边。
• 所有「恶魔」的「终点」向「超级恶魔节点」连接一条流量为 \infty 的边。

以「城堡」的「起点」为源点，「超级恶魔节点」为汇点，求出最小割。根据最小割最大流定理，求出最大流即可。如果最大流为 \infty，说明答案为 -1。

代码

下面的最大流模板参考自 AtCoder Library 。

[sol1-C++]

namespace atcoder {

namespace internal {

template <class T> struct simple_queue {
    std::vector<T> payload;
    int pos = 0;
    void reserve(int n) { payload.reserve(n); }
    int size() const { return int(payload.size()) - pos; }
    bool empty() const { return pos == int(payload.size()); }
    void push(const T& t) { payload.push_back(t); }
    T& front() { return payload[pos]; }
    void clear() {
        payload.clear();
        pos = 0;
    }
    void pop() { pos++; }
};

}  // namespace internal

}  // namespace atcoder

namespace atcoder {

template <class Cap> struct mf_graph {
  public:
    mf_graph() : _n(0) {}
    explicit mf_graph(int n) : _n(n), g(n) {}

    int add_edge(int from, int to, Cap cap) {
        // printf("edge = %d %d %d\n", from, to, cap);
        assert(0 <= from && from < _n);
        assert(0 <= to && to < _n);
        assert(0 <= cap);
        int m = int(pos.size());
        pos.push_back({from, int(g[from].size())});
        int from_id = int(g[from].size());
        int to_id = int(g[to].size());
        if (from == to) to_id++;
        g[from].push_back(_edge{to, to_id, cap});
        g[to].push_back(_edge{from, from_id, 0});
        return m;
    }

    struct edge {
        int from, to;
        Cap cap, flow;
    };

    edge get_edge(int i) {
        int m = int(pos.size());
        assert(0 <= i && i < m);
        auto _e = g[pos[i].first][pos[i].second];
        auto _re = g[_e.to][_e.rev];
        return edge{pos[i].first, _e.to, _e.cap + _re.cap, _re.cap};
    }
    std::vector<edge> edges() {
        int m = int(pos.size());
        std::vector<edge> result;
        for (int i = 0; i < m; i++) {
            result.push_back(get_edge(i));
        }
        return result;
    }
    void change_edge(int i, Cap new_cap, Cap new_flow) {
        int m = int(pos.size());
        assert(0 <= i && i < m);
        assert(0 <= new_flow && new_flow <= new_cap);
        auto& _e = g[pos[i].first][pos[i].second];
        auto& _re = g[_e.to][_e.rev];
        _e.cap = new_cap - new_flow;
        _re.cap = new_flow;
    }

    Cap flow(int s, int t) {
        return flow(s, t, std::numeric_limits<Cap>::max());
    }
    Cap flow(int s, int t, Cap flow_limit) {
        assert(0 <= s && s < _n);
        assert(0 <= t && t < _n);
        assert(s != t);

        std::vector<int> level(_n), iter(_n);
        internal::simple_queue<int> que;

        auto bfs = [&]() {
            std::fill(level.begin(), level.end(), -1);
            level[s] = 0;
            que.clear();
            que.push(s);
            while (!que.empty()) {
                int v = que.front();
                que.pop();
                for (auto e : g[v]) {
                    if (e.cap == 0 || level[e.to] >= 0) continue;
                    level[e.to] = level[v] + 1;
                    if (e.to == t) return;
                    que.push(e.to);
                }
            }
        };
        auto dfs = [&](auto self, int v, Cap up) {
            if (v == s) return up;
            Cap res = 0;
            int level_v = level[v];
            for (int& i = iter[v]; i < int(g[v].size()); i++) {
                _edge& e = g[v][i];
                if (level_v <= level[e.to] || g[e.to][e.rev].cap == 0) continue;
                Cap d =
                    self(self, e.to, std::min(up - res, g[e.to][e.rev].cap));
                if (d <= 0) continue;
                g[v][i].cap += d;
                g[e.to][e.rev].cap -= d;
                res += d;
                if (res == up) return res;
            }
            level[v] = _n;
            return res;
        };

        Cap flow = 0;
        while (flow < flow_limit) {
            bfs();
            if (level[t] == -1) break;
            std::fill(iter.begin(), iter.end(), 0);
            Cap f = dfs(dfs, t, flow_limit - flow);
            if (!f) break;
            flow += f;
        }
        return flow;
    }

    std::vector<bool> min_cut(int s) {
        std::vector<bool> visited(_n);
        internal::simple_queue<int> que;
        que.push(s);
        while (!que.empty()) {
            int p = que.front();
            que.pop();
            visited[p] = true;
            for (auto e : g[p]) {
                if (e.cap && !visited[e.to]) {
                    visited[e.to] = true;
                    que.push(e.to);
                }
            }
        }
        return visited;
    }

  private:
    int _n;
    struct _edge {
        int to, rev;
        Cap cap;
    };
    std::vector<std::pair<int, int>> pos;
    std::vector<std::vector<_edge>> g;
};

}  // namespace atcoder


class Solution {
private:
    static constexpr int dirs[4][2] = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };
    static constexpr int INF = 20010;
    
public:
    int guardCastle(vector<string>& grid) {
        int n = grid[0].size();
        // extra point for collecting portals & demons
        // portal=n*4, demons=n*4+1
        atcoder::mf_graph<int> g(n * 4 + 2);
        int sx = -1, sy = -1;
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < n; ++j) {
                int base_id = i * n + j;
                if(grid[i][j]=='#') continue;
                if (grid[i][j] == '.') {
                    g.add_edge(base_id * 2, base_id * 2 + 1, 1);
                }
                else if (grid[i][j] == 'C') {
                    g.add_edge(base_id * 2, base_id * 2 + 1, INF);
                    sx = i;
                    sy = j;
                }
                else if (grid[i][j] == 'S' || grid[i][j] == 'P') {
                    g.add_edge(base_id * 2, base_id * 2 + 1, INF);
                }
                
                if (grid[i][j] == 'S') {
                    g.add_edge(base_id * 2 + 1, n * 4 + 1, INF);
                }
                if (grid[i][j] == 'P') {
                    g.add_edge(base_id * 2 + 1, n * 4, INF);
                    g.add_edge(n * 4, base_id * 2, INF);
                }
                for (int d = 0; d < 4; ++d) {
                    int ii = i + dirs[d][0];
                    int jj = j + dirs[d][1];
                    if (ii >= 0 && ii < 2 && jj >= 0 && jj < n) {
                        if (grid[ii][jj] == '#') {
                            continue;
                        }
                        int case_id = ii * n + jj;
                        g.add_edge(base_id * 2 + 1, case_id * 2, INF);
                    }
                }
            }
        }
        
        int ans = g.flow((sx * n + sy) * 2, n * 4 + 1);
        if (ans == INF) {
            ans = -1;
        }
        return ans;
    }
};

方法二：动态规划

提示 1

如果「恶魔」能够走到「传送门」，那么「恶魔」就会支配所有的「传送门」。
因此，我们可以考虑两种情况：即允许「恶魔」走到「传送门」，或者不允许「恶魔」走到「传送门」。

• 对于第一种情况，我们可以将所有的「传送门」全部看成「恶魔」；
• 对于第二种情况，我们可以将所有的「传送门」全部看成「城堡」。

此时，网格中就只有「城堡」「恶魔」「空地」「障碍物」了，我们需要做的就是把「城堡」和「恶魔」之间互相分开。

提示 2

使用两次动态规划解决上述问题，每一次动态规划考虑一种情况。

思路

在动态规划之前（将「传送门」替换成「恶魔」或「城堡」之后），我们首先需要判断网格中是否有相邻的「城堡」和「恶魔」。如果有，那么显然是无法将它们分开的，因此无解；如果没有，那么把所有的「空地」都放上「障碍物」，显然可以将它们分开的，因此存在解。

用 f[i][s_1][s_2] 表示当前处理到第 i 列，并且第 i 列的两个格子的状态分别是 s_1 和 s_2 时，最小需要将「空地」放上「障碍物」的操作次数。状态有 4 种：

• 0 表示「空地」
• 1 表示「城堡」或者之前的列存在「城堡」可以到达此位置
• 2 表示「恶魔」或者之前的列存在「恶魔」可以到达此位置
• 3 表示「障碍物」

任意两种状态之间都是相互独立的。

使用该状态的表示方法进行动态规划即可，其中的细节较为复杂，希望读者可以结合下面的细节部分以及代码部分自行思考。

细节

这里介绍一种相对容易实现的状态转移方法。

设第 i-1 列的 f 状态为 s_1 和 s_2，第 i 列本身的两个格子（不考虑第 i-1 列的影响）的状态为 t_1 和 t_2，我们需要判断 s_1, s_2 是否可以和 t_1, t_2 成为相邻的两列。如果可以，那么 s_1, s_2 会对 t_1, t_2 产生影响（例如 s_1=1 且 t_1=0，那么「城堡」就可以到达 t_1 的位置，会将 t_1 的值更新为 1）。设影响后的状态为 t_1’, t_2’，那么就有状态转移方程：

f[i][t_1’][t_2’] = \min\big{ f[i-1][s_1][s_2] + \Delta(t_1, t_2) \big}

其中 \Delta(t_1, t_2) 表示我们额外在第 i 列放置的「障碍物」数量。

代码

[sol2-C++]

int f[10010][4][4];

class Solution {
private:
    static constexpr int dirs[4][2] = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };

public:
    int check(const vector<string>& grid) {
        int n = grid[0].size();
        // check if no (castle, demon) neighbor pair exists
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < n; ++j) {
                for (int d = 0; d < 4; ++d) {
                    int ni = i + dirs[d][0];
                    int nj = j + dirs[d][1];
                    if (ni >= 0 && ni < 2 && nj >= 0 && nj < n) {
                        if (grid[i][j] == 'C' && grid[ni][nj] == 'S') {
                            return INT_MAX;
                        }
                        if (grid[i][j] == 'S' && grid[ni][nj] == 'C') {
                            return INT_MAX;
                        }
                    }
                }
            }
        }

        // f[i][s1][s2] = ith column, s1, s2, minimum barriers to put
        // s1, s2 = (0=empty, 1=castle, 2=demon, 3=stone)
        memset(f, 0x3f, sizeof(f));
        f[0][0][0] = 0;
        unordered_map<char, int> rep = { {'.', 0}, {'C', 1}, {'S', 2}, {'#', 3} };

        auto update = [&](int i, int s1, int s2, int t1, int t2, int extra) {
            if (s1 == 1 || s1 == 2) {
                if (s1 + t1 == 3) {
                    return;
                }
                if (t1 == 0) {
                    t1 = s1;
                }
            }
            if (s2 == 1 || s2 == 2) {
                if (s2 + t2 == 3) {
                    return;
                }
                if (t2 == 0) {
                    t2 = s2;
                }
            }
            if ((t1 == 1 || t1 == 2) && (t1 + t2 == 3)) {
                return;
            }
            if ((t1 == 1 || t1 == 2) && t2 == 0) {
                t2 = t1;
            }
            if ((t2 == 1 || t2 == 2) && t1 == 0) {
                t1 = t2;
            }
            f[i][t1][t2] = min(f[i][t1][t2], f[i - 1][s1][s2] + extra);
        };

        for (int i = 1; i <= n; ++i) {
            int t1 = rep[grid[0][i - 1]];
            int t2 = rep[grid[1][i - 1]];
            for (int s1 = 0; s1 < 4; ++s1) {
                for (int s2 = 0; s2 < 4; ++s2) {
                    update(i, s1, s2, t1, t2, 0);
                    if (grid[0][i - 1] == '.') {
                        update(i, s1, s2, 3, t2, 1);
                    }
                    if (grid[1][i - 1] == '.') {
                        update(i, s1, s2, t1, 3, 1);
                    }
                    if (grid[0][i - 1] == '.' && grid[1][i - 1] == '.') {
                        update(i, s1, s2, 3, 3, 2);
                    }
                }
            }
        }

        int ans = INT_MAX;
        for (int i = 0; i < 4; ++i) {
            for (int j = 0; j < 4; ++j) {
                ans = min(ans, f[n][i][j]);
            }
        }
        return ans;
    }

    int guardCastle(vector<string>& grid) {
        int n = grid[0].size();
        int ans = INT_MAX;

        // mark every portal as castle
        auto g1 = grid;
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < n; ++j) {
                if (g1[i][j] == 'P') {
                    g1[i][j] = 'C';
                }
            }
        }
        ans = min(ans, check(g1));

        // mark every portal as demon
        auto g2 = grid;
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < n; ++j) {
                if (g2[i][j] == 'P') {
                    g2[i][j] = 'S';
                }
            }
        }
        ans = min(ans, check(g2));

        if (ans == INT_MAX) {
            ans = -1;
        }
        return ans;
    }
};