LCP 42-玩具套圈

「力扣挑战赛」场地外，小力组织了一个套玩具的游戏。所有的玩具摆在平地上，toys[i] 以 [xi,yi,ri] 的形式记录了第 i
个玩具的坐标 (xi,yi) 和半径 ri。小扣试玩了一下，他扔了若干个半径均为 r 的圈，circles[j] 记录了第 j
个圈的坐标 (xj,yj)。套圈的规则如下： - 若一个玩具被某个圈完整覆盖了（即玩具的任意部分均在圈内或者圈上），则该玩具被套中。 -
若一个玩具被多个圈同时套中，最终仅计算为套中一个玩具请帮助小扣计算，他成功套中了多少玩具。 注意： -
输入数据保证任意两个玩具的圆心不会重合，但玩具之间可能存在重叠。 示例 1： > 输入：toys = [[3,3,1],[3,2,1]], circles = [[4,3]], r = 2 > > 输出：1 > > 解释：如图所示，仅套中一个玩具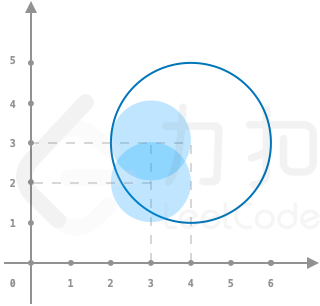
示例
2： > 输入：toys = [[1,3,2],[4,3,1],[7,1,2]], circles = [[1,0],[3,3]], r = 4 >

输出：2 > > 解释：如图所示，套中两个玩具 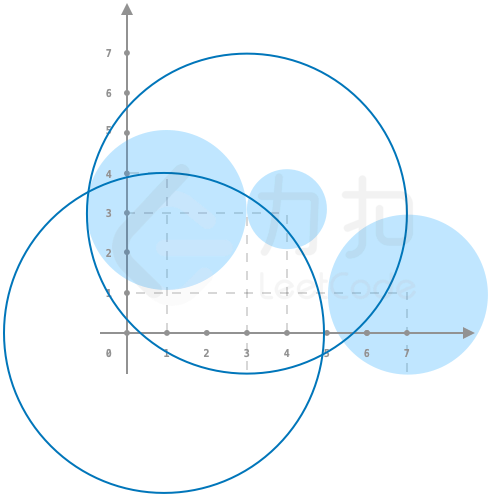![image.png](https://pic.leetcode-
cn.com/1629194157-RiOAuy-image.png){:width=”400px”} 提示： - 1 <= toys.length <= 10^4 - 0 <= toys[i][0], toys[i][1] <= 10^9 - 1 <= circles.length <= 10^4 - 0 <= circles[i][0], circles[i][1] <= 10^9 - 1 <= toys[i][2], r <= 10

LCP的Hard题实际难度不到Hard可真的罕见啊（目前能确定的仅有此题，另外LCP48有嫌疑）……

直接用二重循环枚举每个玩具和每个圈显然会TLE，需要做优化。一个玩具能被套住，需要满足圈和玩具的位置关系是内含，内切或者重合，而且如果不是重合，圈的半径必须更大。根据初中数学知识，这要求两个圆的圆心距离不能超过两个圆的半径差，设套圈半径rc，玩具半径rt，圆心距为d，则必须有d<=rc-rt。

由于rc最大只能是10，而rt至少是1，同时圆心坐标全部为整数，所以能满足d<=rc-rt的圆心的数量极其有限，这样这个题的思路就有了：先把所有套圈的圆心位置放进哈希集合，然后对每一个玩具，枚举所有能让d<=rc-rt的可能的圆心位置，并逐个判断这个位置是否在套圈圆心集合中，只要有一个位置在，就说明这个玩具被套住了，答案加1。

代码实现中，为了方便连续跳出循环，使用一个函数来判断一个玩具能否被套住。

class Solution:
    def circleGame(self, toys: List[List[int]], circles: List[List[int]], r: int) -> int:

        cirs = set()
        for x,y in circles: #所有套圈的圆心进哈希集合
            cirs.add((x,y))

        def check(tx,ty,dif):
            for cx in range(tx-dif,tx+dif+1):
                for cy in range(ty-dif,ty+dif+1):
                    #注意由于圆形区难以枚举，实际枚举的是该圆形区外切的正方形区，要判断一下是否真的是圆心距小于半径差
                    if (cx-tx)*(cx-tx)+(cy-ty)*(cy-ty)<=dif*dif and (cx,cy) in cirs:
                        return True
            return False
        
        ans = 0
        for tx,ty,tr in toys:
            ans+=check(tx,ty,r-tr) #如果套圈比玩具小，check函数根本不会循环，直接就False了，无需特判
        return ans

时间复杂度：O(n+m * C^2),m为玩具的数量，n为圈的数量，C为圈半径和玩具半径的最大差值。预处理需要O(n)的时间，枚举每个玩具需要O(m * C^2)的时间。
空间复杂度：O(n)，哈希表占用的空间由套圈数量决定。