LCP 43-十字路口的交通

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 11:24:04 2023-09-13 11:24:04 Updated    

前往「力扣挑战赛」场馆的道路上，有一个拥堵的十字路口，该十字路口由两条双向两车道的路交叉构成。由于信号灯故障，交警需要手动指挥拥堵车辆。假定路口没有新的来车且一辆车从一个车道驶入另一个车道所需的时间恰好为一秒钟，长度为
4 的一维字符串数组 directions 中按照 东、南、西、北 顺序记录了四个方向从最靠近路口到最远离路口的车辆计划开往的方向。其中： -
"E" 表示向东行驶； - "S" 表示向南行驶； - "W" 表示向西行驶； - "N" 表示向北行驶。
交警每秒钟只能指挥各个车道距离路口最近的一辆车，且每次指挥需要满足如下规则： - 同一秒钟内，一个方向的车道只允许驶出一辆车； -
同一秒钟内，一个方向的车道只允许驶入一辆车； - 同一秒钟内，车辆的行驶路线不可相交。 请返回最少需要几秒钟，该十字路口等候的车辆才能全部走完。
各个车道驶出的车辆可能的行驶路线如图所示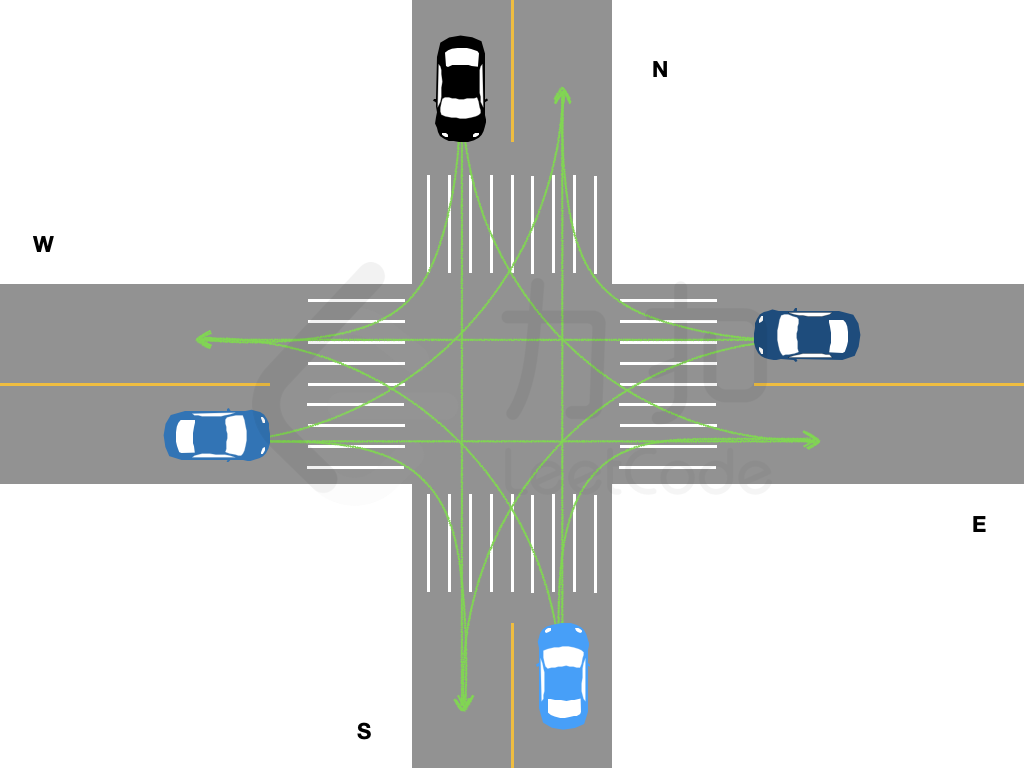： ![图片.png](https://pic.leetcode-
cn.com/1630393755-gyPeMM-%E5%9B%BE%E7%89%87.png){:height=”350px”} 注意： -
测试数据保证不会出现掉头行驶指令，即某一方向的行驶车辆计划开往的方向不会是当前车辆所在的车道的方向; - 表示堵塞车辆行驶方向的字符串仅用大写字母
"E"，"N"，"W"，"S" 表示。 示例 1： >输入：directions = ["W","N","ES","W"] >

输出：2 > >解释： >第 1 秒：东西方向排在最前的车先行，剩余车辆状态 ["","N","S","W"]； >第 2
秒：南、西、北方向的车行驶，路口无等待车辆； >因此最少需要 2 秒，返回 2。 示例 2： >输入：directions = ["NS","WE","SE","EW"] > >输出：3 > >解释： >第 1 秒：四个方向排在最前的车均可驶出； >第 2
秒：东南方向的车驶出，剩余车辆状态 ["","","E","W"]； >第 3 秒：西北方向的车驶出。 提示： -
directions.length = 4 - 0 <= directions[i].length <= 20

【使用的算法】

  1. 动态规划。
  2. 位运算。

【计算步骤】

  1. 设输入的char *direction[4]的四个字符串的长度依次为len0、len1、len2和len3。其中0、1、2、3依次表示东南西北四个方向。
  2. 定义一个四维数组，dp[1 + len0][1 + len1][1 + len2][1 + len3]，其中，dp[x[0]][x[1]][x[2]][x[3]]表示四个方向依次剩余x[0]、x[1]、x[2]和x[3]辆车的时候，最少的通行时间。
    当方向i剩余x[i]辆车的时候，排在路口的那辆车在数组中的下标为index[i] = leni - x[i]，当x[i] == 0，即index[i] == leni的时候，表示这个方向没有任何剩余车辆了。
    最终要得到的结果，就是dp[len0][len1][len2][len3]。
    边界条件为：dp[0][0][0][0] = 0，即没有任何剩余车辆时，需要的时间为0。
  3. 用一个二进制掩码t来记录dp[x[0]][x[1]][x[2]][x[3]]对应的四个方向的路口，是否还有剩余车辆。
    掩码右数第i位比特（从第0开始计）用来表示这个方向i是否还有剩余车辆，该位为1表示有剩余车辆。
    遍历这个掩码的每一个非空子集mask，即选中这个掩码中的一部分车辆进行通行：
    (1) 如果选中的这些车辆，相互的行进方向产生了冲突，即行进路线有相交，或者驶入同一个目标车道，则忽略这一次的子集。
    (2) 如果选中的这些车辆，相互的行进方向互不冲突，则这一秒钟作为这个子集的车辆的行进耗时，各个方向上还剩余y[0]、y[1]、y[2]和y[3]辆车，于是可得：
    dp[x[0]][x[1]][x[2]][x[3]] = MIN_VAL(dp[x[0]][x[1]][x[2]][x[3]], 1 + dp[y[0]][y[1]][y[2]][y[3]]);
    这里：如果选中的子集中，包含了方向i的车辆，y[i] = x[i] - 1，否则，y[i] = x[i]，用位运算的表达方式是：
    y[i] = (1 << i & mask) ? x[i] - 1 : x[i];
  4. 上面第3步中提到了，需要判断选中的某个子集，各辆车的行进方向是否产生冲突。这里将输入的原始字符串数组direction[4]进行归一化处理，即将原数组中出现的绝对方向东南西北（即”ESWN”四个字母），转换成相对方向左前右，即left、straight、right三个词的首字母”LSR”，记录在数组dir[4]里。
    如此，对于任意一个方向的车辆，都可以归一化处理。
    (1) 当这个方向的车辆需要左转时，会和左向来的“直行或左转”车辆、对向来的“直行或右转”车辆、右向来的“直行或左转”车辆产生冲突。
    (2) 当这个方向的车辆需要直行时，会和左向来的“直行或左转”车辆、对向来的“左转”车辆、右向来的“所有”车辆产生冲突。
    (3) 当这个方向的车辆需要右转时，会和左向来的“直行”车辆、对向来的“左转”车辆产生冲突。

20230602122312.png{:width=400}

【代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
#define MIN_VAL(x, y)   ((x) < (y) ? (x) : (y))

static bool checkConflict(char **dir, int *index, int mask);

/* 掩码mask一共4位，右数0、1、2、3位依次表示选中东南西北四个方向。
里面的size0，size1，size2，size3，是在各自的length基础上加一，一来是最终的动态规划数组的下标要用到各自的length，而来，部分length可能为0，加一确保不会出现声明0长度的数组。
临时变量d0、d1、d2、d3、dir[4]，是对输入的directions[4]字符串做归一化处理的，即将绝对方向东南西北转换成相对方向左前右。 */
int trafficCommand(char **directions, int directionsSize)
{
    /* 初始化memset使用的一个超大值，记录为topValue，必须是各个字节位相等的数值。 */
    const int topValue = 0x7F7F7F7F, len0 = strlen(directions[0]), len1 = strlen(directions[1]), len2 = strlen(directions[2]), len3 = strlen(directions[3]), size0 = len0 + 1, size1 = len1 + 1, size2 = len2 + 1, size3 = len3 + 1;
    int t = 0, mask = 0;
    int x[4], y[4], index[4];
    char d0[size0], d1[size1], d2[size2], d3[size3], *dir[4];
    bool flag = false;
    int dp[size0][size1][size2][size3];
    /* 初始化，及边界条件。 */
    memset(dp, topValue, sizeof(dp));
    dp[0][0][0][0] = 0;
    dir[0] = d0;
    dir[1] = d1;
    dir[2] = d2;
    dir[3] = d3;
    /* 归一化处理，将每个方向上，所有的E、S、W、N转换成左转L、右转R和直行S。 */
    /* 东边来车。 */
    for(t = 0; len0 > t; t++)
    {
        /* 向南是左转，向北是右转，向西是直行。 */
        d0[t] = ('S' == directions[0][t]) ? 'L' : (('N' == directions[0][t]) ? 'R' : 'S');
    }
    d0[t] = '\0';
    /* 南边来车。 */
    for(t = 0; len1 > t; t++)
    {
        /* 向西是左转，向东是右转，向北是直行。 */
        d1[t] = ('W' == directions[1][t]) ? 'L' : (('E' == directions[1][t]) ? 'R' : 'S');
    }
    d1[t] = '\0';
    /* 西边来车。 */
    for(t = 0; len2 > t; t++)
    {
        /* 向北是左转，向南是右转，向东是直行。 */
        d2[t] = ('N' == directions[2][t]) ? 'L' : (('S' == directions[2][t]) ? 'R' : 'S');
    }
    d2[t] = '\0';
    /* 北边来车。 */
    for(t = 0; len3 > t; t++)
    {
        /* 向东是左转，向西是右转，向南是直行。 */
        d3[t] = ('E' == directions[3][t]) ? 'L' : (('W' == directions[3][t]) ? 'R' : 'S');
    }
    d3[t] = '\0';
    /* 开始动态规划，四层循环遍历。index[i]在这里表示在这个方向还剩余x[i]辆车时，头部的车辆的下标。
    当index[i]越界时，即index[i] >= leni时，表示这个方向没有剩余车辆了。 */
    for(x[0] = 0; size0 > x[0]; x[0]++)
    {
        index[0] = len0 - x[0];
        for(x[1] = 0; size1 > x[1]; x[1]++)
        {
            index[1] = len1 - x[1];
            for(x[2] = 0; size2 > x[2]; x[2]++)
            {
                index[2] = len2 - x[2];
                for(x[3] = 0; size3 > x[3]; x[3]++)
                {
                    index[3] = len3 - x[3];
                    /* 四个方向是否确实还剩余有车，t对应比特位是0的话，表示这个方向无车。对应于index[i] >= leni。 */
                    t = (0 < x[0]) | (0 < x[1]) << 1 | (0 < x[2]) << 2 | (0 < x[3]) << 3;
                    /* 遍历掩码t的所有非空子集mask。空集没有意义，因为哪辆车都不选的话，等于在浪费当前这一秒。
                    遍历子集时，循环语句中用到了这一句：mask = mask - 1 & t，这是快速遍历非空子集的位运算方法。 */
                    for(mask = t; 0 < mask; mask = mask - 1 & t)
                    {
                        /* 判断选中的车辆之中，通行方向是否有交叉，或同时进入同一目标车道。
                        其中index[i] >= leni对应的方向i，其mask中的比特位必然为0，所以在子函数中使用时，不用担心数组越界。 */
                        flag = checkConflict(dir, index, mask);
                        if(false == flag)
                        {
                            /* 如果未产生冲突，则计算y[]长度。即方向i上通过了第index[i]辆车，i方向数量剩余x[i] - 1，
                            否则，这个方向没有车辆或者没有被选中，仍然为x[i]辆车。 */
                            y[0] = (1 & mask) ? x[0] - 1 : x[0];
                            y[1] = (2 & mask) ? x[1] - 1 : x[1];
                            y[2] = (4 & mask) ? x[2] - 1 : x[2];
                            y[3] = (8 & mask) ? x[3] - 1 : x[3];
							/* 其中1秒钟用于选中的mask子集过路口，剩余的dp[y[0]][y[1]][y[2]][y[3]]在前面遍历过程中已经计算过。 */
                            dp[x[0]][x[1]][x[2]][x[3]] = MIN_VAL(dp[x[0]][x[1]][x[2]][x[3]], 1 + dp[y[0]][y[1]][y[2]][y[3]]);
                        }
                    }
                }
            }
        }
    }
    /* 如果最终结果仍然是初始化的最大值，那不妨就一辆一辆单独过，总能够全部过去的。 */
    t = (topValue == dp[len0][len1][len2][len3]) ? len0 + len1 + len2 + len3 : dp[len0][len1][len2][len3];
    return t;
}

/* 检查当前位置的车辆，选中掩码mask时，前进方向和目标车道是否产生冲突，有冲突就返回true。
这里，“冲突”的含义，包含了题目中描述的路径有交叉，以及驶入同一目标车道两种情况。 */
static bool checkConflict(char **dir, int *index, int mask)
{
    int x = 0, left = 0, right = 0, straight = 0;
    /* 查看各个方向来车。 */
    for(x = 0; mask >= 1 << x; x++)
    {
        /* 如果这个方向有来车，则把它的左向、右向、对向的索引列出，依次为left、straight、right。 */
        if(mask & 1 << x)
        {
            left = x + 1 & 0x03;
            straight = x + 2 & 0x03;
            right = x + 3 & 0x03;
            /* 本方向左转。 */
            if('L' == dir[x][index[x]])
            {
                /* 会和左向来的“直行或左转”车辆、对向来的“直行或右转”车辆、右向来的“直行或左转”车辆产生冲突。 */
                if(((1 << left & mask) && ('S' == dir[left][index[left]] || 'L' == dir[left][index[left]]))
                    || ((1 << straight & mask) && ('S' == dir[straight][index[straight]] || 'R' == dir[straight][index[straight]]))
                    || ((1 << right & mask) && ('S' == dir[right][index[right]] || 'L' == dir[right][index[right]])))
                {
                    return true;
                }
            }
            /* 本方向直行。 */
            else if('S' == dir[x][index[x]])
            {
                /* 会和左向来的“直行或左转”车辆、对向来的“左转”车辆、右向来的“所有”车辆产生冲突。 */
                if(((1 << left & mask) && ('S' == dir[left][index[left]] || 'L' == dir[left][index[left]]))
                    || ((1 << straight & mask) && ('L' == dir[straight][index[straight]]))
                    || (1 << right & mask))
                {
                    return true;
                }
            }
            /* 本方向右转。 */
            else
            {
                /* 会和左向来的“直行”车辆、对向来的“左转”车辆产生冲突。 */
                if(((1 << left & mask) && ('S' == dir[left][index[left]]))
                    || ((1 << straight & mask) && ('L' == dir[straight][index[straight]])))
                {
                    return true;
                }
            }
        }
    }
    return false;
}
 Comments
On this page
LCP 43-十字路口的交通