LCP 52-二叉搜索树染色

欢迎各位勇者来到力扣城，本次试炼主题为「二叉搜索树染色」。每位勇士面前设有一个二叉搜索树的模型，模型的根节点为
root，树上的各个节点值均不重复。初始时，所有节点均为蓝色。现在按顺序对这棵二叉树进行若干次操作， ops[i] = [type, x, y]
表示第 i 次操作为： + type 等于 0 时，将节点值范围在 [x, y] 的节点均染蓝 + type 等于 1
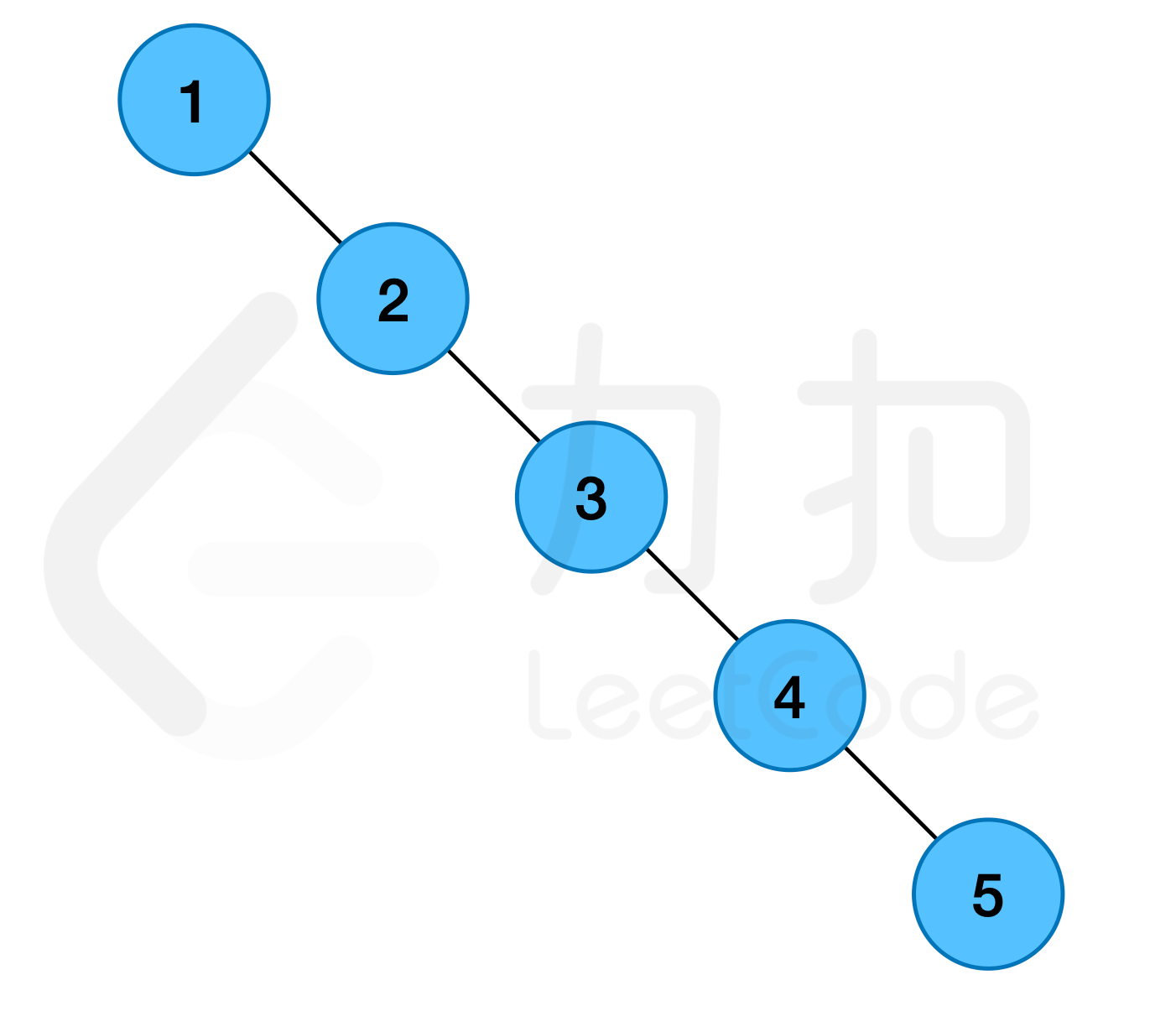
时，将节点值范围在 [x, y] 的节点均染红请返回完成所有染色后，该二叉树中红色节点的数量。 注意： + 题目保证对于每个操作的
x、y 值定出现在二叉搜索树节点中 示例 1： >输入：root = [1,null,2,null,3,null,4,null,5], ops = [[1,2,4],[1,1,3],[0,3,5]] > >输出：2 > >解释： >第 0 次操作，将值为 2、3、4 的节点染红； >第
1 次操作，将值为 1、2、3 的节点染红； >第 2 次操作，将值为 3、4、5 的节点染蓝； >因此，最终值为 1、2 的节点为红色节点，返回数量 2
![image.png](https://pic.leetcode-cn.com/1649833948-arSlXd-
image.png){:width=230px} 示例 2： >输入：root = [4,2,7,1,null,5,null,null,null,null,6] >ops = [[0,2,2],[1,1,5],[0,4,5],[1,5,7]] > >输出：5 > >解释： >第 0 次操作，将值为 2 的节点染蓝； >第 1
次操作，将值为 1、2、4、5 的节点染红； >第 2 次操作，将值为 4、5 的节点染蓝； >第 3 次操作，将值为 5、6、7 的节点染红；

因此，最终值为 1、2、5、6、7 的节点为红色节点，返回数量 5 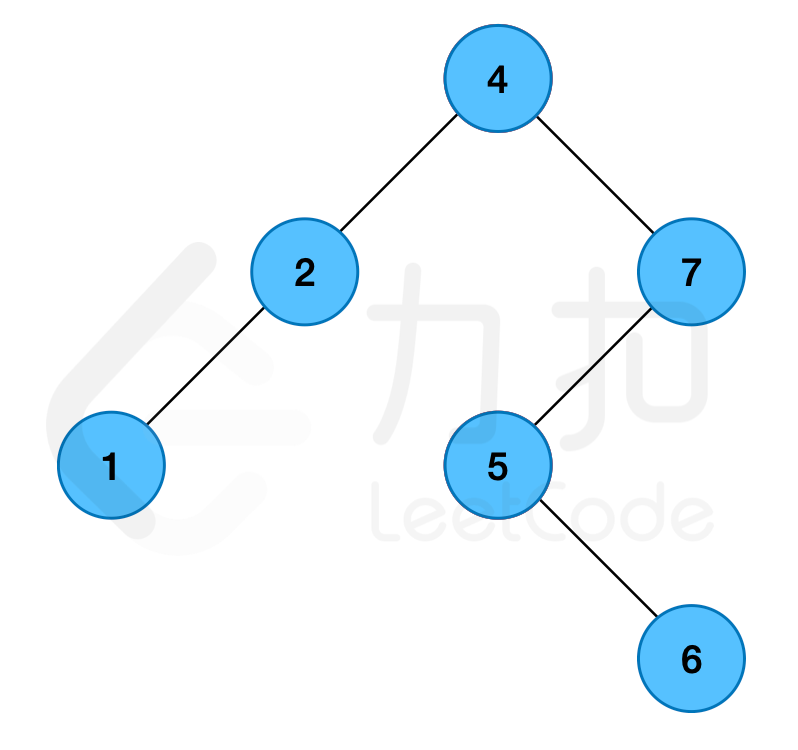![image.png](https://pic.leetcode-
cn.com/1649833763-BljEbP-image.png){:width=230px} 提示： + 1 <= 二叉树节点数量 <= 10^5 + 1 <= ops.length <= 10^5 + ops[i].length == 3 + ops[i][0] 仅为
0 or 1 + 0 <= ops[i][1] <= ops[i][2] <= 10^9 + 0 <= 节点值 <= 10^9

解法：模拟

其实和二叉搜索树一点关系都没有。

每个点的颜色只取决于最后一次包含该点的操作。用 set 维护所有颜色待确定的点，倒序处理询问，每次利用 lower_bound 方法从 set 中取出所有在询问范围内的点染色后删掉。因为每个点只会被删掉一次，所以总体复杂度 \mathcal{O}((n + q)\log n)，其中 n 是节点数量，q 是询问数量。

参考代码（c++）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
    set<int> st;

    void dfs(TreeNode *node) {
        if (node == nullptr) return;
        st.insert(node->val);
        dfs(node->left);
        dfs(node->right);
    }

public:
    int getNumber(TreeNode* root, vector<vector<int>>& ops) {
        dfs(root);
        int ans = 0;
        for (int i = (int) ops.size() - 1; i >= 0; i--) {
            while (true) {
                auto it = st.lower_bound(ops[i][1]);
                if (it == st.end() || (*it) > ops[i][2]) break;
                st.erase(it);
                if (ops[i][0]) ans++;
            }
        }
        return ans;
    }
};