LCP 54-夺回据点

欢迎各位勇者来到力扣城，本次试炼主题为「夺回据点」。魔物了占领若干据点，这些据点被若干条道路相连接，roads[i] = [x, y] 表示编号
x、y 的两个据点通过一条道路连接。现在勇者要将按照以下原则将这些据点逐一夺回： - 在开始的时候，勇者可以花费资源先夺回一些据点，初始夺回第
j 个据点所需消耗的资源数量为 cost[j] -
接下来，勇者在不消耗资源情况下，每次可以夺回一个和「已夺回据点」相连接的魔物据点，并对其进行夺回 >
注：为了防止魔物暴动，勇者在每一次夺回据点后（包括花费资源夺回据点后），需要保证剩余的所有魔物据点之间是相连通的（不经过「已夺回据点」）。
请返回勇者夺回所有据点需要消耗的最少资源数量。 注意： - 输入保证初始所有据点都是连通的，且不存在重边和自环 示例 1： >输入：

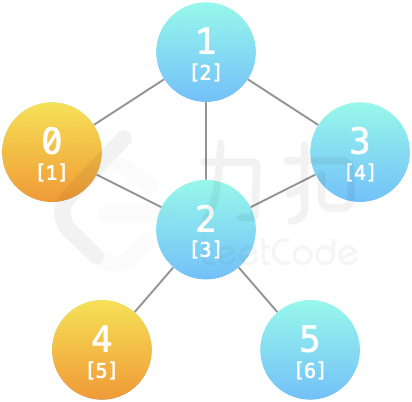
cost = [1,2,3,4,5,6] >roads = [[0,1],[0,2],[1,3],[2,3],[1,2],[2,4],[2,5]]

输出：6 > >解释： >勇者消耗资源 6 夺回据点 0 和 4，魔物据点 1、2、3、5 相连通； >第一次夺回据点
1，魔物据点 2、3、5 相连通； >第二次夺回据点 3，魔物据点 2、5 相连通； >第三次夺回据点 2，剩余魔物据点 5；
第四次夺回据点 5，无剩余魔物据点； >因此最少需要消耗资源为 6，可占领所有据点。
![image.png](https://pic.leetcode-cn.com/1648706944-KJstUN-
image.png){:height=170px} 示例 2： >输入： >cost = [3,2,1,4] >roads = [[0,2],[2,3],[3,1]] > >输出：2 > >解释： >勇者消耗资源 2 夺回据点 1，魔物据点 0、2、3 相连通；
第一次夺回据点 3，魔物据点 2、0 相连通； >第二次夺回据点 2，剩余魔物据点 0； >第三次夺回据点 0，无剩余魔物据点；
因此最少需要消耗资源为 2，可占领所有据点。 ![image.png](https://pic.leetcode-
cn.com/1648707186-LJRwzU-image.png){:height=60px} 提示： - 1 <= roads.length, cost.length <= 10^5 - 0 <= roads[i][0], roads[i][1] < cost.length - 1 <= cost[i] <= 10^9

解法：点双连通分量缩点

要求保留连通性，很容易想到点双连通分量和割点。

简化问题：树上的情况

首先考虑简化问题：题目给出的是一棵树，并按要求夺回据点。

容易发现，一开始只能选择叶子节点（选非叶子节点树直接不连通），而且若这棵树有 k 个叶子，我们至少选择其中的 (k - 1) 个。因此我们选择权值最小的 (k - 1) 个叶子即可。

原问题

将所有点双连通分量缩点得到一棵树，题目转换为树上的情况。每个点的权值是该双连通分量中非割点权值的最小值。

这个做法的正确性建立在如下事实的基础上：

考虑一个单独的点双连通分量，一开始只需要选一个点，就能合法地占领整个点双连通分量；
点双连通分量缩点后得到的一定是一棵树；
缩点后得到的树的叶子一定不是原图中的割点。

~~证明留给读者思考~~。

参考代码（c++）

class Solution {
    const int S = 0;
    int n;

    vector<vector<int>> e;
    vector<bool> isCut;
    vector<int> dfn, low;
    int clk = 0;
    stack<int> stk;
    // 所有点双连通分量
    vector<vector<int>> dcc;

    void tarjan(int sn) {
        dfn[sn] = low[sn] = ++clk;
        stk.push(sn);
        int flag = 0;
        for (int fn : e[sn]) {
            if (!dfn[fn]) {
                tarjan(fn);
                low[sn] = min(low[sn], low[fn]);
                if (low[fn] >= dfn[sn]) {
                    flag++;
                    if (sn != S || flag > 1) isCut[sn] = true;
                    int t;
                    dcc.push_back(vector<int>());
                    do {
                        t = stk.top(); stk.pop();
                        dcc.back().push_back(t);
                    } while (t != fn);
                    dcc.back().push_back(sn);
                }
            } else low[sn] = min(low[sn], dfn[fn]);
        }
    }

public:
    long long minimumCost(vector<int>& cost, vector<vector<int>>& roads) {
        n = cost.size();
        if (n == 1) return cost[0];

        e = vector<vector<int>>(n);
        for (auto &r : roads) e[r[0]].push_back(r[1]), e[r[1]].push_back(r[0]);
        isCut = vector<bool>(n);
        dfn = low = vector<int>(n);
        tarjan(S);

        // 整张图是一个双连通分量，选择整张图权值最小的点即可
        if (dcc.size() == 1) {
            int ans = 2e9;
            for (int x : cost) ans = min(ans, x);
            return ans;
        }

        vector<int> vec;
        for (auto &c : dcc) {
            int cnt = 0, mn = 2e9;
            for (int x : c) {
                if (isCut[x]) cnt++;
                else mn = min(mn, cost[x]);
            }
            // 该双连通分量只和一个割点相连，是缩点形成的树的叶子节点
            if (cnt == 1) vec.push_back(mn);
        }
        sort(vec.begin(), vec.end());
        long long ans = 0;
        for (int i = 0; i + 1 < vec.size(); i++) ans += vec[i];
        return ans;
    }
};