LCP 60-力扣泡泡龙

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 17:01:06 2023-09-13 17:01:06 Updated    

欢迎各位勇者来到力扣城，本次试炼主题为「力扣泡泡龙」。 游戏初始状态的泡泡形如二叉树
root，每个节点值对应了该泡泡的分值。勇者最多可以击破一个节点泡泡，要求满足： - 被击破的节点泡泡 至多 只有一个子节点泡泡 -
当被击破的节点泡泡有子节点泡泡时，则子节点泡泡将取代被击破泡泡的位置 > 注：即整棵子树泡泡上移
请问在击破一个节点泡泡操作或无击破操作后，二叉泡泡树的最大「层和」是多少。 注意： - 「层和」为同一高度的所有节点的分值之和 示例 1：

输入：root = [6,0,3,null,8] > > 输出：11 > > 解释：勇者的最佳方案如图所示
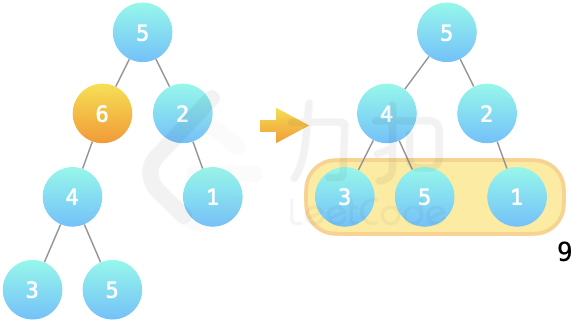
![image.png](https://pic.leetcode-cn.com/1648180809-XSWPLu-
image.png){:height=”100px”} 示例 2： > 输入：root = [5,6,2,4,null,null,1,3,5]

输出：9 > > 解释：勇者击破 6 节点，此时「层和」最大为 3+5+1 = 9
![image.png](https://pic.leetcode-cn.com/1648180769-TLpYop-
image.png){:height=”200px”} 示例 3： > 输入：root = [-5,1,7] > > 输出：8 > >
解释：勇者不击破节点，「层和」最大为 1+7 = 8 提示： - 2 <= 树中节点个数 <= 10^5 - -10000 <= 树中节点的值 <= 10000

一份用例 26 杀的故事

在浏览题解时，发现大部分题解都提到了两个剪枝的方式来避免 TLE：

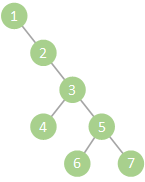
image.png

  1. 如果树中存在 “链式结构”，那么只需要考虑删除它的最顶端的节点对整棵树的影响。比如上图的节点 1 和节点 2，那么只需考虑删除节点 1，因为删除节点 1 对整棵树的影响，已经把删除节点 2 的囊括了。
  2. 如果某个可删除的节点，在某层导致着整个层级的节点上浮，那么无需继续考虑这个节点。如删除上图的节点 3，会导致第 4 层的 4,5 俩节点上浮，但是节点 4,5 上移，相当于删除该层级，然后让后续层级上浮，对答案没有影响。

于是我构造了下面这个测试用例：

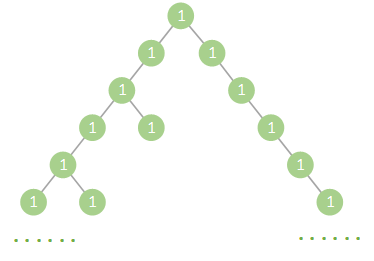
image.png

这个用例的特点是，

  • 总共包含 99998 个节点（包含 1 个根节点）；
  • 左侧每间隔 1 个节点，向右分叉 1 个，这个是针对优化 1 的；共有 59998 个节点；
  • 右侧是一条单链表，是用来针对优化 2 的；共有 39999 个节点；

下面附上这个用例的构造代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
TreeNode* generate() {
  TreeNode* root = new TreeNode(1);
  TreeNode* cur = root;
  for(int i = 0; i < 39999; ++i) {
    cur->left = new TreeNode(1);
    cur = cur->left;
  }
  cur = root;
  for(int i = 0; i < 39999; ++i) {
    cur->right = new TreeNode(1);
    cur = cur->right;
  }
  cur = root;
  for(int i = 0; i < 39999; ++i) {
    cur = cur->left;
    if(i & 1) cur->right = new TreeNode(1);
  }
  return root;
}

然后就是大家喜闻乐见的大杀特杀环节了！

总结一下，这道题的真正解决方法，应当是 启发式合并(O(nlogn))，或者 树链剖分 (O(n))，
或者，我在下面也给大家一种 O(n) 的思路（包含证明）。

O(n) 解法 - 基本思路

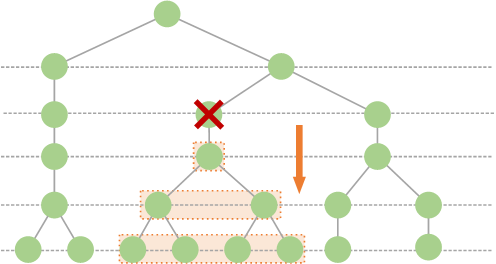
首先可以很容易看出来，如果删掉了一个节点，那么会造成下面的每一层的一个 “管辖区间” 被替换成更下层的 “管辖区间”。那么很直接的思路就是，首先枚举可以被删除的节点；然后，依次向下遍历其管辖的 “节点区间”，从而计算每一层的替换后的层和，如下图所示：

image.png

为此，我们可以首先进行一次 dfs，对每个节点，收集以下信息（参考下图）：

  1. 当前节点在当前层的前缀和 sum；
  2. 当前节点的下一层，从左侧开始，第一个 属于该节点（或更右侧的节点）的节点 lptr；
  3. 当前节点的下一层，从右侧开始，第一个 属于该节点（或更左侧的节点）的节点 rptr。

利用 lptr 和 rptr，我们可以从一个 “管辖区间” 移动到更下一层的 “管辖区间”，如刚下图所描述的那样。

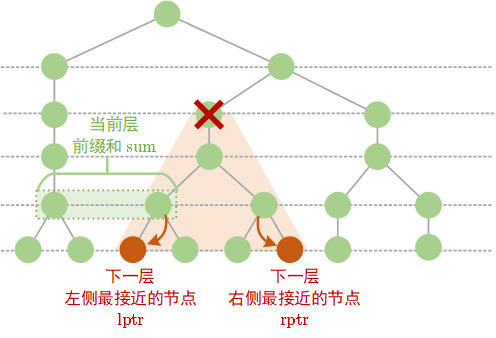
image.png

对每一个 “管辖区间”，如果上移，那么它对当前层和的影响是：新的层和 = 当前层和 - 当前 “管辖区间” 的和 + 下一层 “管辖区间” 的和。

O(n) 优化

上面的算法，复杂度是 O(nh) 的，因为对每个可删除节点，都需要遍历到树的底部。不过，只要加上一个小的剪枝优化，那么可以让时间复杂度变为 O(n)。

优化方案是：如果向下遍历 “管辖区间” 时，遇到了 之前已经遍历过 的 “管辖区间”，那么就停止遍历。

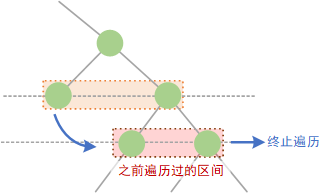
image.png

因为，如果这个区间之前遍历过，那么，它再往下的所有区间肯定也都被遍历过，再遍历就是重复劳动，没有意义。

时间复杂度为 O(n) 的证明附后。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
class Solution {
public:
    vector<vector<tuple<int, int, int, int>>> level_infs; /* 前缀和，占用，左下指针，右下指针 */
    vector<pair<int, int>> remove_list;
    int collect(int level, TreeNode* node) {
        if(!node) 
            return 0;

        while(level + 1 >= level_infs.size())
            level_infs.push_back({ {0, -1, -1, -1} });

        level_infs[level].emplace_back(
            get<0>(level_infs[level].back()) + node->val, /* 前缀和 */
            -1, /* 被占用的情况 */
            level_infs[level+1].size(), /* 左侧向下指针 */
            -1 /* 右侧向下指针(需要等遍历完之后再补充) */
        );
        node->val = level_infs[level].size() - 1;

        if(collect(level + 1, node->left) + collect(level + 1, node->right) != 2) 
            remove_list.emplace_back((int)level_infs[level].size() - 1, level);
        
        get<3>(level_infs[level].back()) = (int)level_infs[level + 1].size() - 1;

        return 1;
    }
    int getMaxLayerSum(TreeNode* root) {
        collect(0, root);

        int height = (int)level_infs.size() - 1, res = INT_MIN;
        for(int level = 0; level < height; ++level)
            res = max(res, get<0>(level_infs[level].back()));

        for(int idx = 0; idx < remove_list.size(); ++idx) {
            auto [node, start] = remove_list[idx];
            int left = node, right = node;
            int lost = get<0>(level_infs[start][left]) - get<0>(level_infs[start][left-1]);
            for(int level = start; level < height; ++level) {
                if(left > right) 
                    break;

                /* 如果当前 "管辖区间" 为整层的节点，那么没有必要继续遍历下去，它相当于删除该层 */
                /* 另外，这个优化还能避坑 "如果最后一层全删掉，那么这个和为 0 是没有意义的" */
                if(right - left + 1 == level_infs[level].size() - 1)
                    break;

                auto& [lsum, luse, ne_left, _unused1] = level_infs[level][left];
                auto& [rsum, ruse, _unused2, ne_right] = level_infs[level][right];

                /* 剪枝：如果当前区间已经被使用过，则跳过后续部分 */
                if(luse != -1 && luse == ruse)
                    break;
                luse = ruse = idx;

                int add = 0;
                if(ne_left <= ne_right)
                    add = get<0>(level_infs[level+1][ne_right]) - get<0>(level_infs[level+1][ne_left - 1]);

                res = max(res, get<0>(level_infs[level].back()) - lost + add);

                left = ne_left, right = ne_right, lost = add;
            }
        }

        return res;
    }
};

附：O(n) 的证明

结论： 对于每一层，若其节点个数为 m，那么作用于其之上的 不同的 “管辖区间” 的数目，不会超过 2m - 1。
证明： 首先，对于同一层节点的两个不同的 “管辖区间”，依次命名为 “区间 a” 和 “区间 b”，分别由两个不同的节点 “节点 A” 和 “节点 B” 管辖，那么，

  • 如果节点 A 是 节点 B 的祖先，那么区间 A 包含 区间 B；
  • 如果节点 B 是 节点 A 的祖先，那么区间 B 包含 区间 A；
  • 如果节点 A 和 节点 B 没有祖孙关系，那么区间 A 和 B 没有交集。

我们可以看到，不同的 “管辖区间” 之间要么存在包含关系，要么没有交集。因此，如果我们按照 区间长度 从小到大遍历 “管辖区间”，那么：

  • 首先被考虑的是所有长度为 1 的区间（也就是节点本身，自己管自己），总共有 m 个；
  • 然后从小到大考虑长度不为 1 的区间，每个区间一定包含至少 2 个更小的区间，可以认为是大的区间 “合并” 了更小的区间。而这样的合并操作最多发生 m-1 次，即区间数目不超过 m-1。

加起来不会超过 2m - 1。

由结论易得，若整个图中含有 n 个节点，那么总的不同的区间个数不会超过 2n。

 Comments
On this page
LCP 60-力扣泡泡龙
  1. 一份用例 26 杀的故事
  2. O(n) 解法 - 基本思路
  3. O(n) 优化
  4. 代码
  5. 附：O(n) 的证明