力扣嘉年华的花店中从左至右摆放了一排鲜花，记录于整型一维矩阵 flowers
中每个数字表示该位置所种鲜花的品种编号。你可以选择一段区间的鲜花做成插花，且不能丢弃。在你选择的插花中，如果每一品种的鲜花数量都不超过 cnt
朵，那么我们认为这束插花是「美观的」。 > - 例如：[5,5,5,6,6] 中品种为 5 的花有 3 朵，品种为 6 的花有 2
朵，每一品种 的数量均不超过 3 请返回在这一排鲜花中，共有多少种可选择的区间，使得插花是「美观的」。 注意： - 答案需要以
1e9 + 7 (1000000007) 为底取模，如：计算初始结果为：1000000008，请返回 1 示例 1：

输入：flowers = [1,2,3,2], cnt = 1 > >输出：8 > >解释：相同的鲜花不超过 1 朵，共有 8
种花束是美观的； >长度为 1 的区间 [1]、[2]、[3]、[2] 均满足条件，共 4 种可选择区间 >长度为 2 的区间
[1,2]、[2,3]、[3,2] 均满足条件，共 3 种可选择区间 >长度为 3 的区间 [1,2,3] 满足条件，共 1
种可选择区间。 >区间 [2,3,2],[1,2,3,2] 都包含了 2 朵鲜花 2 ，不满足条件。 >返回总数 4+3+1 = 8
示例 2： >输入：flowers = [5,3,3,3], cnt = 2 > >输出：8 提示： - 1 <= flowers.length <= 10^5 - 1 <= flowers[i] <= 10^5 - 1 <= cnt <= 10^5

菜鸡第一次写题解用来锻炼自己的语言能力，望看到的伙伴们见谅┭┮﹏┭┮

题目理解：

·就是给你一个数组 flowers 和一个正整数 cnt 。

·数组 flowers 存在某些非空子数组，这些子数组里面的每个数字出现的次数不能超过 cnt 。

·返回这些子数组的总数量。

算法流程：

①一个滑动窗口，左指针 left，右指针 right 。

②初始化整型变量 ans 作为满足条件的数组数量，哈希表 count 记录滑动窗口中数字的出现次数。

③ right 一直往右遍历。

④假如：滑动窗口右侧新加进的数字 x 符合要求(即 count[x]<=cnt )，则整个滑动窗口也满足题目条件要求的子数组。

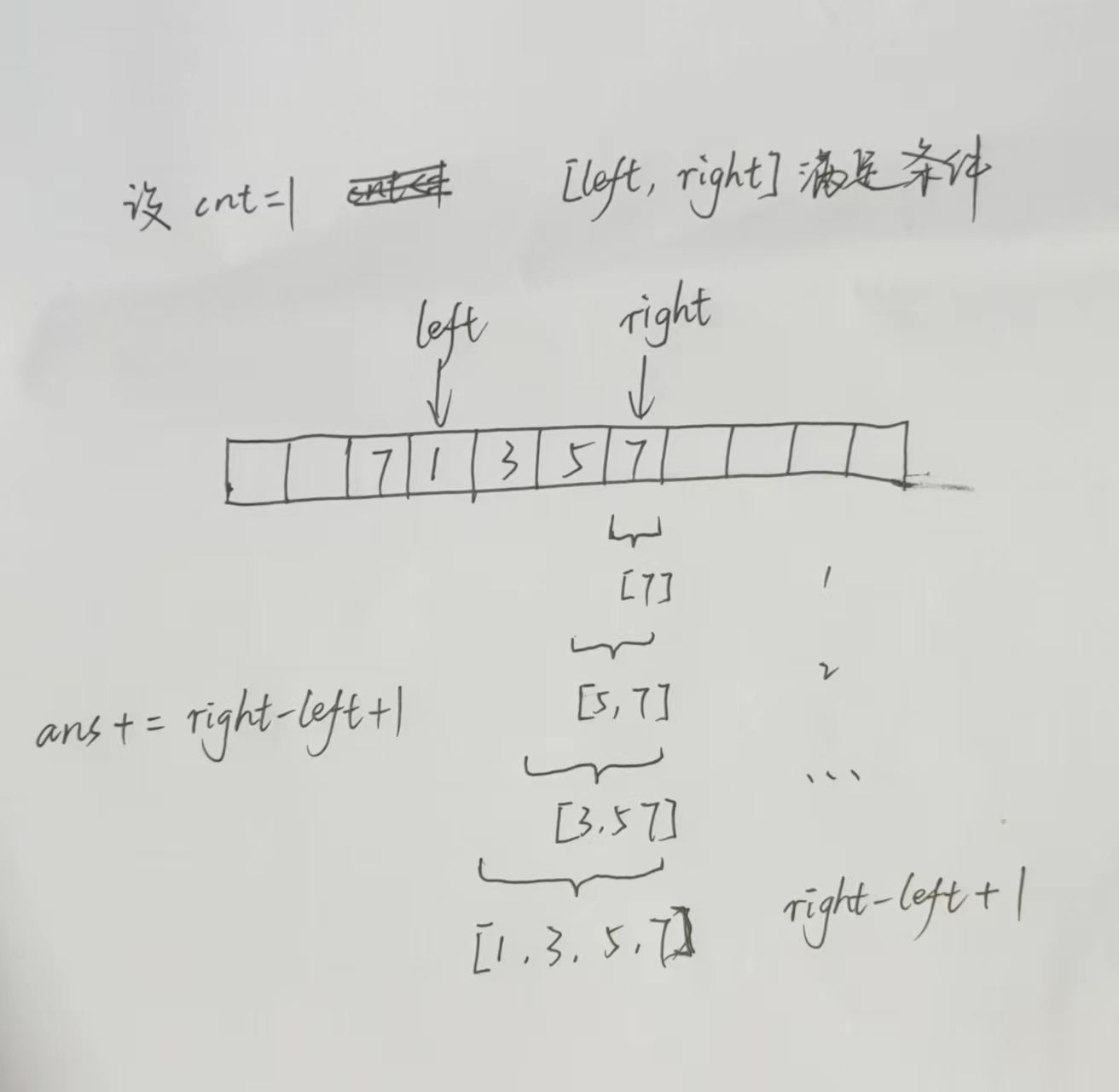
⑤ ans 增加，增加的数目为 right-left+1，原因如图片所示：包含右侧新数字的符合题目要求的区间个数 (倒着数)。

⑥假如：滑动窗口右侧新加进的数字 x 不符合要求(即 count[x]>cnt )，则整个滑动窗口不满足题目条件要求的子数组。

⑦ left 开始遍历，滑动数组逐个排出左侧数字 y ，滑动窗口数字 y 出现次数减少，则 –count[y] 。

⑧直到遇到滑动窗口的左侧第一个数字 x，数字 x 的出现次数减少，count[–x]<=cnt 使得滑动窗口再次满足题目条件要求的子数组。

⑨ ans 增加，增加的数目为 right-left+1，原因如图片所示：包含右侧新数字的符合题目要求的区间个数 (倒着数)。

⑩ right 继续遍历，直到末尾停下。

ans增加：

·既然滑动窗口的这个数组符合条件，那么它的子数组也符合条件

·右侧元素是新来的，那 ans 新增加的数目就是包括右侧新元素的子数组

代码：

class Solution {
public:
    int beautifulBouquet(vector<int>& flowers, int cnt) {
        int mod=1e9+7;
        int ans=0;                                //计算结果
        unordered_map<int,int> count;             //记录滑动窗口中数字的出现次数
        for(int left=0,right=0;right<flowers.size();++right)     
        {                                         //右指针一直往右遍历
            ++count[flowers[right]];              //遍历数字的出现字数 +1
            while(count[flowers[right]]>cnt)      //假如右指针新遍历的 数字x 不满足条件 (数字x的出现次数大于cnt)
            {                                     //则移动左指针，直到遇到滑动窗口中 数字x 的第一次出现
                --count[flowers[left]];           //左指针往右移动，那滑动窗口弹出数字的出现次数 -1
                ++left;                           //左指针一直往右移动   
            }                                     //原本count[x]>cnt, 当左指针遇到x，count[x]-1<=cnt，跳出循环
            ans+=right-left+1;                           
            ans%=mod;                             //ans增加，数目为 包含新的数字x的符合题目要求的区间个数(倒着数)
        }
        return ans;
    }
};

LCP 68-美观的花束

题目理解：

算法流程：

ans增加：

代码：