LCP 70-沙地治理

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:45:43 2023-09-13 16:45:43 Updated    

在力扣城的沙漠分会场展示了一种沙柳树，这种沙柳树能够将沙地转化为坚实的绿地。 展示的区域为正三角形，这片区域可以拆分为若干个子区域，每个子区域都是边长为
1 的小三角形，其中第 i 行有 2i - 1 个小三角形。
初始情况下，区域中的所有位置都为沙地，你需要指定一些子区域种植沙柳树成为绿地，以达到转化整片区域为绿地的最终目的，规则如下： -
若两个子区域共用一条边，则视为相邻；

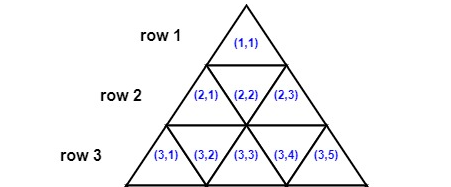
如下图所示，(1,1)和(2,2)相邻，(3,2)和(3,3)相邻；(2,2)和(3,3)不相邻，因为它们没有共用边。 -
若至少有两片绿地与同一片沙地相邻，则这片沙地也会转化为绿地 - 转化为绿地的区域会影响其相邻的沙地
image.png 现要将一片边长为
size 的沙地全部转化为绿地，请找到任意一种初始指定 最少 数量子区域种植沙柳的方案，并返回所有初始种植沙柳树的绿地坐标。 示例 1：
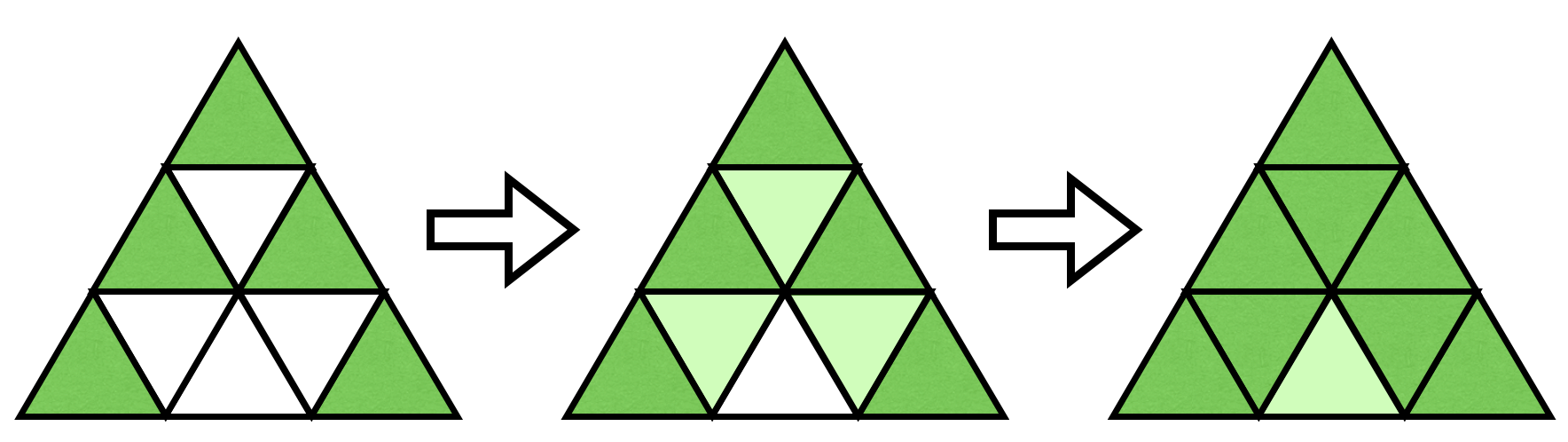
输入：size = 3 >输出：[[1,1],[2,1],[2,3],[3,1],[3,5]] >解释：如下图所示，一种方案为： >指定所示的 5
个子区域为绿地。 >相邻至少两片绿地的 (2,2)，(3,2) 和 (3,4) 演变为绿地。 >相邻两片绿地的 (3,3) 演变为绿地。
![image.png](https://pic.leetcode-cn.com/1662692503-ncjywh-
image.png){:width=500px} 示例 2： >输入：size = 2 >输出：[[1,1],[2,1],[2,3]]
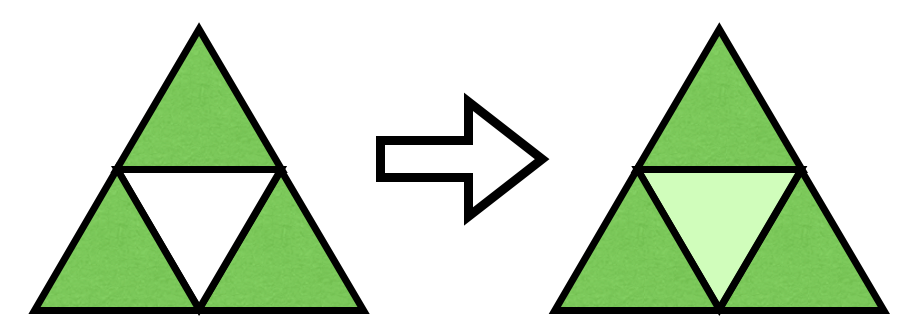
解释：如下图所示： >指定所示的 3 个子区域为绿地。 >相邻三片绿地的 (2,2) 演变为绿地。
![image.png](https://pic.leetcode-cn.com/1662692507-mgFXRj-
image.png){:width=276px} 提示： - 1 <= size <= 1000

解法：找规律

从选手的角度来说，本题只要找规律猜结论即可。但是从题解的角度来说，还是应该给出解法的证明。因此这里尝试给出证明。

下述参考代码将会构造一个长度是 \lfloorn^2 + 3n + 2/4}\rfloor 的答案。因此我们首先需要证明，初始最少需要标记 \lfloorn^2 + 3n + 2/4}\rfloor 个三角形。

我们先来定义“外边”和“内边”：对于所有小三角形的边，与大三角形的边界重合的部分为“外边”，剩下的都叫“内边”。

例如，下图展示了一个 n = 3 的大三角形。红色的边是外边，黑色的边是内边。容易得知，小三角形共有 n^2 个，外边有 3n 条。

e.png

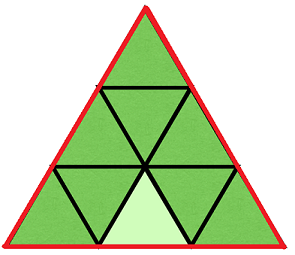
根据题意，当一个未标记的小三角形与两个已标记的小三角形相邻时，该小三角形也被标记。另外，当一个初始未被标记的小三角形变为标记状态时，由于它的两条边已经被消耗掉了，它只剩一条边可以继续标记其它三角形。也就是说：

消耗两条内边可以得到一个小三角形，以及一条外边或内边。

设一开始共标记了 x 个小三角形，这些小三角形共有 a_0 条外边；之后第一轮新标记的小三角形共有 a_1 条外边，第二轮新标记的小三角形共有 a_2 条外边，…，我们有不等式：

\begin{matrix}
n^2 & \le & x + 3x - a_0/2} + 3x - a_0/2} - a_1/2} + 3x - a_0/2} - a_1/2} - a_2/2} + \cdots & \text{生成的小三角形总数需要大等于 } n^2 \
& & & \text{一开始被标记的小三角形有 } 3x - a_0 \text{ 条内边} \
& & & \text{因此可以生成 } 3x - a_0/2} \text{ 个三角形} \
& & & \text{后面生成的三角形只有一条内边可用，因此没有乘以 } 3 \
\
\hline
\
& = & x + \sum\limits_{i=1}^{+\infty}3x}{2^i} - (\sum\limits_{i=1}^{+\infty}a_0/2^i} + \sum\limits_{i=1}^{+\infty}a_1/2^i} + \sum\limits_{i=1}^{+\infty}a_2/2^i} + \cdots) & \text{把分子相同的项整理到一起} \
\
\hline
\
& = & 4x - (a_0 + a_1 + a_2 + \cdots) & \lim\limits_{n \to +\infty}\sum\limits_{i=1}^n 1/2^i} = 1 \
\
\hline
\
& = & 4x - 3n & a_0 + a_1 + a_2 + \cdots \text{ 是外边的总数} \
\end{matrix}

因此有 4x - 3n \ge n^2，即 x \ge n^2 + 3n}{4。

注意到 x 是整数，我们讨论 n \bmod 4 的情况：

  • n \bmod 4 = 0 或 n \bmod 4 = 1，n^2 + 3n}{4 是整数，因此 x 的最小值是 n^2 + 3n}{4。又 \lfloorn^2 + 3n + 2/4}\rfloor = n^2 + 3n}{4} + \lfloor1/2}\rfloor = n^2 + 3n}{4，因此 x \ge \lfloorn^2 + 3n + 2/4}\rfloor 成立。
  • n \bmod 4 = 2 或 n \bmod 4 = 3，n^2 + 3n}{4 的小数部分是 1/2，因此 x 是最小值是 n^2 + 3n}{4} + 1。又 \lfloorn^2 + 3n + 2/4}\rfloor = n^2 + 3n}{4} + 1，因此 x \ge \lfloorn^2 + 3n + 2/4}\rfloor 成立。

这样我们就成功证明了初始最少需要标记 \lfloorn^2 + 3n + 2/4}\rfloor 个三角形。

参考代码（c++）

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    vector<vector<int>> sandyLandManagement(int n) {
        vector<vector<int>> ans;
        for (int i = 1; i < n; i++) for (int j = 1; j <= i * 2 - 1; j += 4) ans.push_back({i, j});
        ans.push_back({n, 1});
        if (n > 1) ans.push_back({n, n * 2 - 1});
        for (int i = 4; i < n * 2 - 1; i += 8) ans.push_back({n, i});
        for (int i = 7; i < n * 2 - 1; i += 8) ans.push_back({n, i});
        for (int i = 9; i < n * 2 - 1; i += 8) ans.push_back({n, i});
        return ans;
    }
};
 Comments
On this page
LCP 70-沙地治理
  1. 解法：找规律
  2. 参考代码（c++）