LCP 71-集水器

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:25 2023-09-13 16:06:25 Updated    

字符串数组 shape 描述了一个二维平面中的矩阵形式的集水器，shape[i][j] 表示集水器的第 i 行 j 列为： -
'l'表示向左倾斜的隔板（即从左上到右下）； - 'r'表示向右倾斜的隔板（即从左下到右上）； - '.' 表示此位置没有隔板
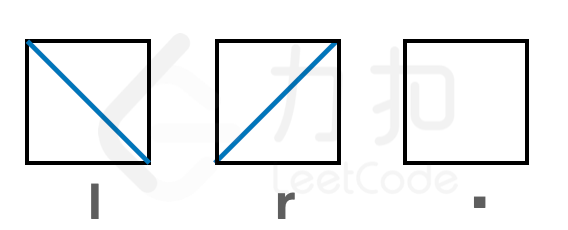![image.png](https://pic.leetcode-cn.com/1664424667-wMnPja-
image.png){:width=200px} 已知当隔板构成存储容器可以存水，每个方格代表的蓄水量为
2。集水器初始浸泡在水中，除内部密闭空间外，所有位置均被水填满。 现将其从水中竖直向上取出，请返回集水器最终的蓄水量。 注意： -
隔板具有良好的透气性，因此空气可以穿过隔板，但水无法穿过 示例 1： > 输入： > shape = ["....rl","l.lr.r",".l..r.","..lr.."] > > 输出：18 > >
解释：如下图所示，由于空气会穿过隔板，因此红框区域没有水 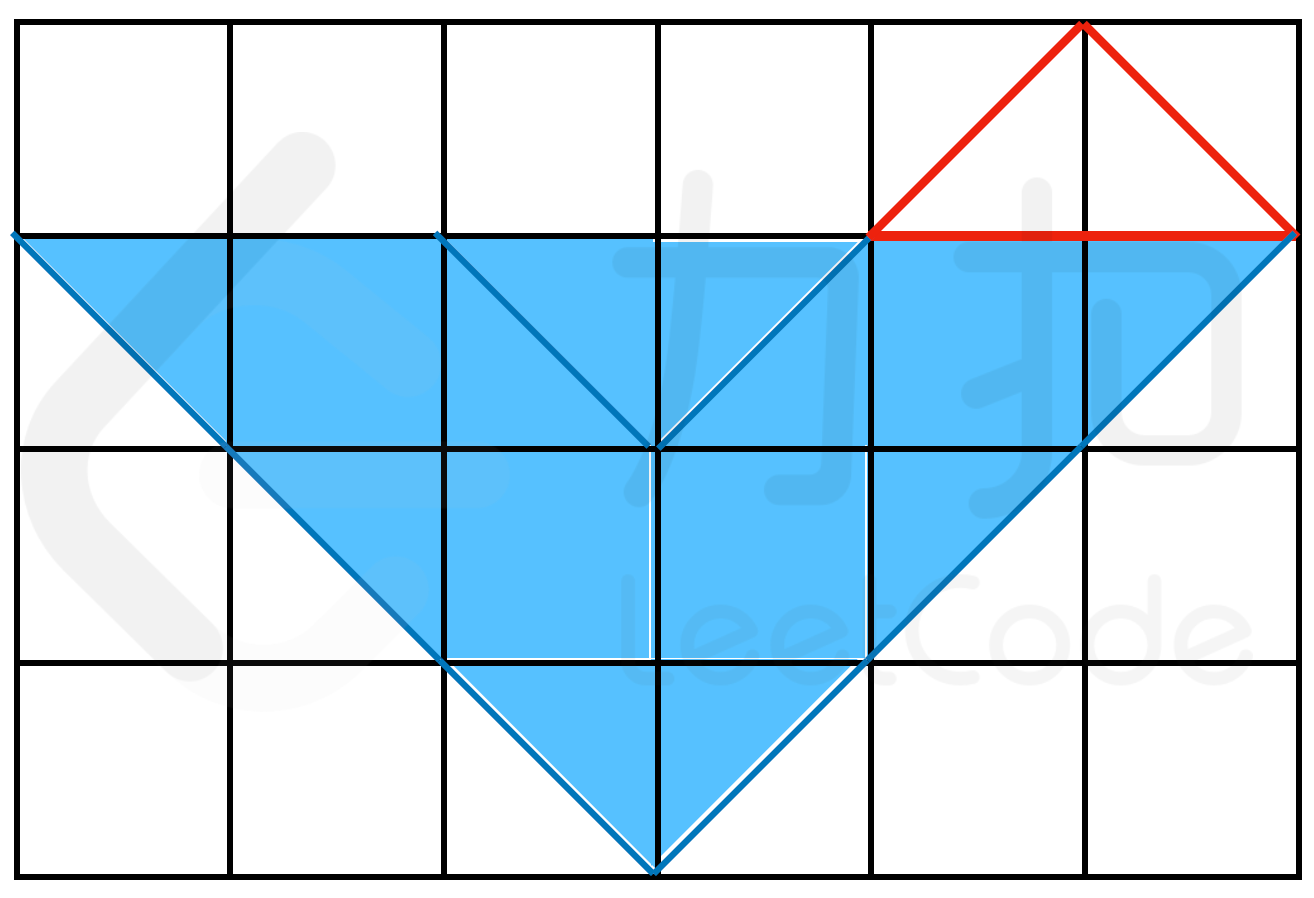![image.png](https://pic.leetcode-
cn.com/1664436239-eyYxeP-image.png){:width=”280px”} 示例 2： > 输入： > shape = [".rlrlrlrl","ll..rl..r",".llrrllrr","..lr..lr."] > 输出：18 > >
解释：如图所示。由于红框右侧未闭合，因此多余的水会从该处流走。 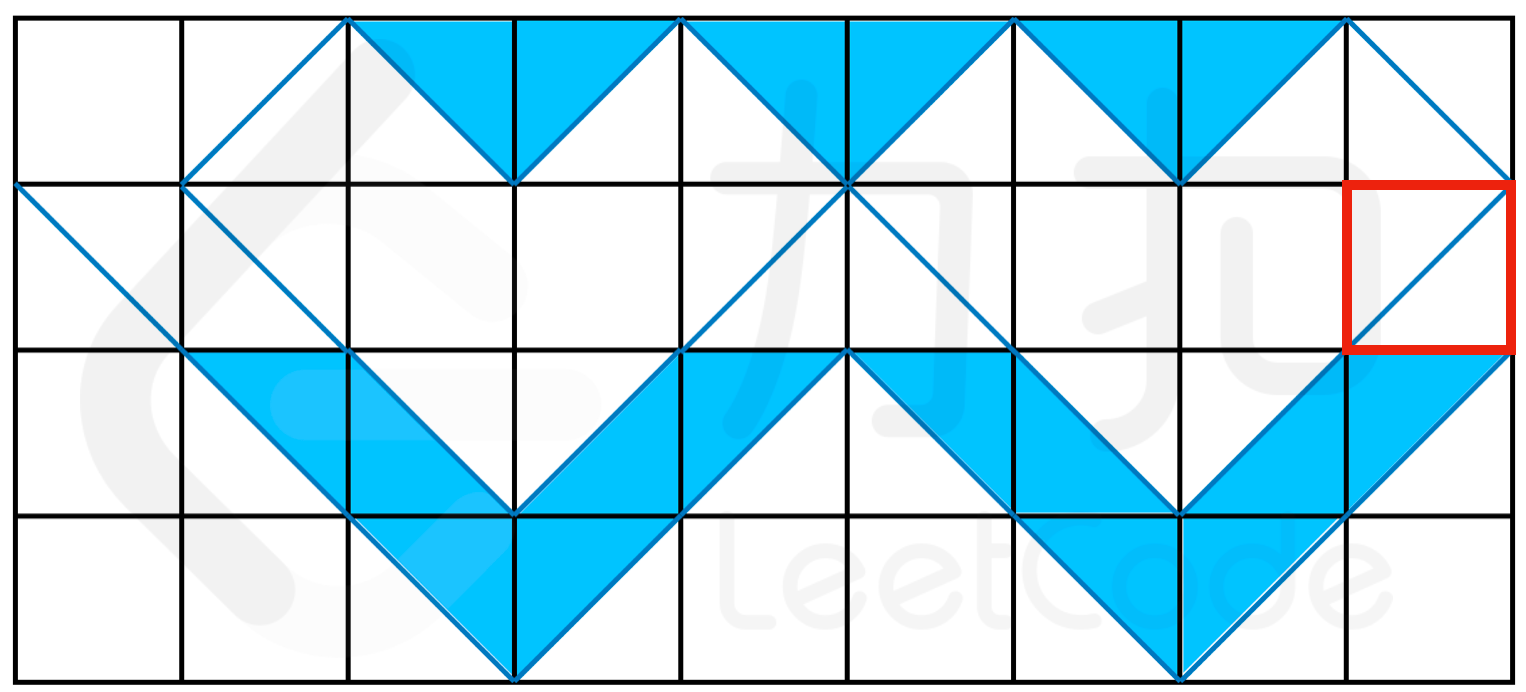![image.png](https://pic.leetcode-
cn.com/1664436082-SibVMv-image.png){:width=”400px”} 示例 3： > 输入： > shape = ["rlrr","llrl","llr."] > 输出：6 > > 解释：如图所示。
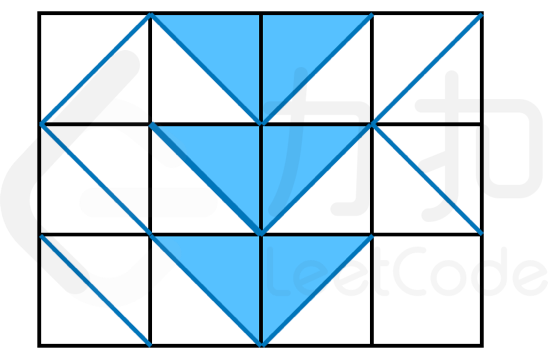![image.png](https://pic.leetcode-cn.com/1664424855-dwpUHO-
image.png){:width=”230px”} 示例 4： > 输入： > shape = ["...rl...","..r..l..",".r.rl.l.","r.r..l.l","l.l..rl.",".l.lr.r.","..l..r..","...lr..."]

输出：30 > > 解释：如下图所示。由于中间为内部密闭空间，无法蓄水。 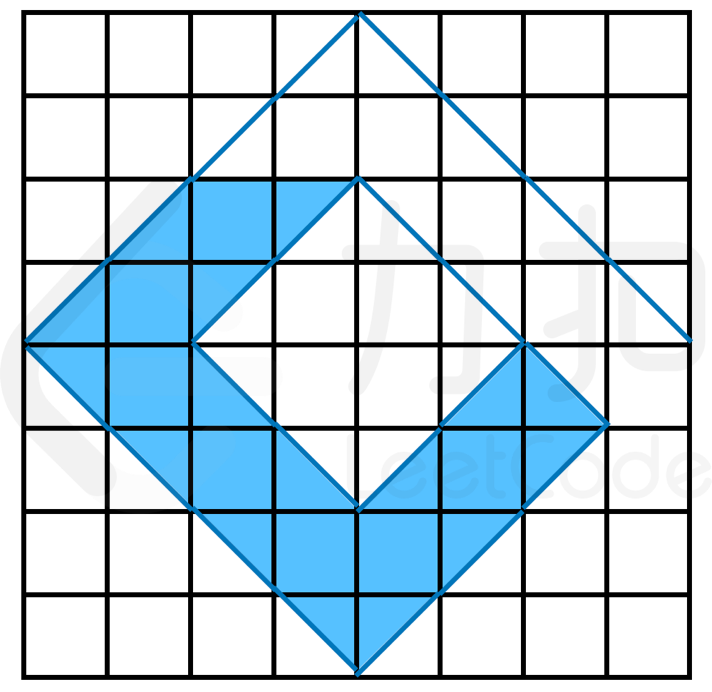![image.png](https://pic.leetcode-
cn.com/1664424894-mClEXh-image.png){:width=”350px”} 提示： - 1 <= shape.length <= 50 - 1 <= shape[i].length <= 50 - shape[i][j] 仅为
'l'、'r' 或 '.'

视频讲解 已出炉，欢迎点赞三连，在评论区分享你对这场力扣杯的看法~

记录关键思路，详细的说明见视频讲解。

  1. 判断能否容纳水：第 i 行的水，在不走到第 i-1 行的前提下，无法触及左、右、下边界。
  2. 转换成连通性问题，用并查集处理。
  3. 为了方便判断是否触及边界，还需要在左、右、下各加一条格子。
  4. 根据 1，我们可以从最后一行往上计算。
  5. 用并查集合并当前行各个区域，以及边界。
  6. 如果合并完了，枚举当前行的各个区域，如果不和边界相连，那么该区域能容纳水。
  7. 边界、最上面一层和超级汇点 0 相连。
  8. 最后判断的时候，如果该区域能容纳水，且和超级汇点相连，那么不是闭合区域，就真的有水。
  9. 统计真的有水的格子，即为答案。
  10. 代码实现时，把每个格子划分四个区域，相对两个区域，代码写起来要容易一些。
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
class Solution:
    def reservoir(self, shape: List[str]) -> int:
        n, m = len(shape), len(shape[0])
        # 每个格子分成四个区域（上下左右），标上序号，方便用并查集连通
        # 假设左右下还有一圈格子，直接连到超级汇点 0
        u = [[0] * (m + 2) for _ in range(n + 1)]
        d = [[0] * (m + 2) for _ in range(n + 1)]
        l = [[0] * (m + 2) for _ in range(n + 1)]
        r = [[0] * (m + 2) for _ in range(n + 1)]
        c = 1
        for i in range(n):
            for j in range(1, m + 1):  # 假设格子的列号从 1 开始，这样方便表示左右边界
                u[i][j] = c; c += 1
                d[i][j] = c; c += 1
                l[i][j] = c; c += 1
                r[i][j] = c; c += 1

        # 并查集模板
        fa = list(range(c))
        def find(x: int) -> int:
            if fa[x] != x:
                fa[x] = find(fa[x])
            return fa[x]
        def merge(x: int, y: int):
            fa[find(x)] = find(y)

        ok = [False] * c  # 能否容纳水
        # 倒着判断每一行，寻找可能有水的区域
        for i in range(n - 1, -1, -1):
            for j in range(m + 1):
                merge(r[i][j], l[i][j + 1])  # 连通左右
            for j, type in enumerate(shape[i], 1):
                merge(d[i][j], u[i + 1][j])  # 连通下
                # 根据格子的类型连接格子内部四个区域
                if type == '.':
                    merge(l[i][j], u[i][j])
                    merge(l[i][j], d[i][j])
                    merge(l[i][j], r[i][j])
                elif type == 'l':
                    merge(l[i][j], d[i][j])
                    merge(r[i][j], u[i][j])
                else:
                    merge(l[i][j], u[i][j])
                    merge(r[i][j], d[i][j])
            for j in range(1, m + 1):
                # 在没有连接第 i-1 行的情况下，无法到达左右下边界 => 能容纳水
                ok[l[i][j]] = find(l[i][j]) != find(0)
                ok[r[i][j]] = find(r[i][j]) != find(0)
                ok[u[i][j]] = find(u[i][j]) != find(0)
                ok[d[i][j]] = find(d[i][j]) != find(0)

        # 第一行连上超级汇点，方便后面统一判断是否在闭合区域里面
        for j in range(1, m + 1):
            merge(u[0][j], 0)

        ans = 0
        for i, b in enumerate(ok):
            if b and find(i) == find(0):  # 能容纳水，且不在闭合区域里面
                ans += 1
        return ans // 2
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
class Solution {
    private int[] fa;

    public int reservoir(String[] shape) {
        int n = shape.length, m = shape[0].length(), c = 1;
        // 每个格子分成四个区域（上下左右），标上序号，方便用并查集连通
        // 假设左右下还有一圈格子，直接连到超级汇点 0
        int[][] u = new int[n + 1][m + 2], d = new int[n + 1][m + 2], l = new int[n + 1][m + 2], r = new int[n + 1][m + 2];
        for (var i = 0; i < n; ++i)
            for (var j = 1; j <= m; ++j) {  // 假设格子的列号从 1 开始，这样方便表示左右边界
                u[i][j] = c++;
                d[i][j] = c++;
                l[i][j] = c++;
                r[i][j] = c++;
            }

        fa = new int[c];
        for (var i = 0; i < c; i++) fa[i] = i;

        var ok = new boolean[c]; // 能否容纳水
        // 倒着判断每一行，寻找可能有水的区域
        for (var i = n - 1; i >= 0; --i) {
            for (var j = 0; j <= m; j++)
                merge(r[i][j], l[i][j + 1]); // 连通左右
            for (var j = 1; j <= m; j++) {
                merge(d[i][j], u[i + 1][j]); // 连通下
                // 根据格子的类型连接格子内部四个区域
                var type = shape[i].charAt(j - 1);
                if (type == '.') {
                    merge(l[i][j], u[i][j]);
                    merge(l[i][j], d[i][j]);
                    merge(l[i][j], r[i][j]);
                } else if (type == 'l') {
                    merge(l[i][j], d[i][j]);
                    merge(r[i][j], u[i][j]);
                } else {
                    merge(l[i][j], u[i][j]);
                    merge(r[i][j], d[i][j]);
                }
            }
            for (var j = 1; j <= m; j++) {
                // 在没有连接第 i-1 行的情况下，无法到达左右下边界 => 能容纳水
                ok[l[i][j]] = find(l[i][j]) != find(0);
                ok[r[i][j]] = find(r[i][j]) != find(0);
                ok[u[i][j]] = find(u[i][j]) != find(0);
                ok[d[i][j]] = find(d[i][j]) != find(0);
            }
        }

        // 第一行连上超级汇点，方便后面统一判断是否在闭合区域里面
        for (var j = 1; j <= m; j++)
            merge(u[0][j], 0);

        var ans = 0;
        for (var i = 0; i < c; i++)
            if (ok[i] && find(i) == find(0))
                ++ans; // 能容纳水，且不在闭合区域里面
        return ans / 2;
    }

    private int find(int x) {
        if (fa[x] != x) fa[x] = find(fa[x]);
        return fa[x];
    }

    private void merge(int x, int y) {
        fa[find(x)] = find(y);
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    int reservoir(vector<string> &shape) {
        int n = shape.size(), m = shape[0].size(), c = 1;
        // 每个格子分成四个区域（上下左右），标上序号，方便用并查集连通
        // 假设左右下还有一圈格子，直接连到超级汇点 0
        int u[n + 1][m + 2], d[n + 1][m + 2], l[n + 1][m + 2], r[n + 1][m + 2];
        memset(u, 0, sizeof(u)); memset(d, 0, sizeof(d)); memset(l, 0, sizeof(l)); memset(r, 0, sizeof(r));
        for (int i = 0; i < n; ++i)
            for (int j = 1; j <= m; ++j) // 假设格子的列号从 1 开始，这样方便表示左右边界
                u[i][j] = c++, d[i][j] = c++, l[i][j] = c++, r[i][j] = c++;

        // 并查集模板
        int fa[c];
        iota(fa, fa + c, 0);
        function<int(int)> find = [&](int x) -> int { return fa[x] == x ? x : fa[x] = find(fa[x]); };
        auto merge = [&](int x, int y) { fa[find(x)] = find(y); };

        bool ok[c]; // 能否容纳水
        memset(ok, 0, sizeof(ok));
        // 倒着判断每一行，寻找可能有水的区域
        for (int i = n - 1; i >= 0; --i) {
            for (int j = 0; j <= m; j++) merge(r[i][j], l[i][j + 1]); // 连通左右
            for (int j = 1; j <= m; j++) {
                merge(d[i][j], u[i + 1][j]); // 连通下
                // 根据格子的类型连接格子内部四个区域
                if (shape[i][j - 1] == '.') merge(l[i][j], u[i][j]), merge(l[i][j], d[i][j]), merge(l[i][j], r[i][j]);
                else if (shape[i][j - 1] == 'l') merge(l[i][j], d[i][j]), merge(r[i][j], u[i][j]);
                else merge(l[i][j], u[i][j]), merge(r[i][j], d[i][j]);
            }
            for (int j = 1; j <= m; j++) {
                // 在没有连接第 i-1 行的情况下，无法到达左右下边界 => 能容纳水
                ok[l[i][j]] = find(l[i][j]) != find(0);
                ok[r[i][j]] = find(r[i][j]) != find(0);
                ok[u[i][j]] = find(u[i][j]) != find(0);
                ok[d[i][j]] = find(d[i][j]) != find(0);
            }
        }

        // 第一行连上超级汇点，方便后面统一判断是否在闭合区域里面
        for (int j = 1; j <= m; j++) merge(u[0][j], 0);

        int ans = 0;
        for (int i = 0; i < c; i++)
            ans += ok[i] && find(i) == find(0); // 能容纳水，且不在闭合区域里面
        return ans / 2;
    }
};
[sol1-Go]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
func reservoir(shape []string) int {
	n, m := len(shape), len(shape[0])
	// 每个格子分成四个区域（上下左右），标上序号，方便用并查集连通
	// 假设左右下还有一圈格子，直接连到超级汇点 0
	u := make([][]int, n+1)
	d := make([][]int, n+1)
	l := make([][]int, n+1)
	r := make([][]int, n+1)
	for i := range u {
		u[i] = make([]int, m+2)
		d[i] = make([]int, m+2)
		l[i] = make([]int, m+2)
		r[i] = make([]int, m+2)
	}
	c := 1
	for i := 0; i < n; i++ {
		for j := 1; j <= m; j++ { // 假设格子的列号从 1 开始，这样方便表示左右边界
			u[i][j] = c; c++
			d[i][j] = c; c++
			l[i][j] = c; c++
			r[i][j] = c; c++
		}
	}

	// 并查集模板
	fa := make([]int, c)
	for i := range fa {
		fa[i] = i
	}
	var find func(int) int
	find = func(x int) int {
		if fa[x] != x {
			fa[x] = find(fa[x])
		}
		return fa[x]
	}
	merge := func(x, y int) { fa[find(x)] = find(y) }

	ok := make([]bool, c) // 能否容纳水
	// 倒着判断每一行，寻找可能有水的区域
	for i := n - 1; i >= 0; i-- {
		for j := 0; j <= m; j++ {
			merge(r[i][j], l[i][j+1]) // 连通左右
		}
		for j := 1; j <= m; j++ {
			merge(d[i][j], u[i+1][j]) // 连通下
			// 根据格子的类型连接格子内部四个区域
			switch shape[i][j-1] {
			case '.':
				merge(l[i][j], u[i][j])
				merge(l[i][j], d[i][j])
				merge(l[i][j], r[i][j])
			case 'l':
				merge(l[i][j], d[i][j])
				merge(r[i][j], u[i][j])
			default:
				merge(l[i][j], u[i][j])
				merge(r[i][j], d[i][j])
			}
		}
		for j := 1; j <= m; j++ {
			// 在没有连接第 i-1 行的情况下，无法到达左右下边界 => 能容纳水
			ok[l[i][j]] = find(l[i][j]) != find(0)
			ok[r[i][j]] = find(r[i][j]) != find(0)
			ok[u[i][j]] = find(u[i][j]) != find(0)
			ok[d[i][j]] = find(d[i][j]) != find(0)
		}
	}

	// 第一行连上超级汇点，方便后面统一判断是否在闭合区域里面
	for j := 1; j <= m; j++ {
		merge(u[0][j], 0)
	}

	ans := 0
	for i, b := range ok {
		if b && find(i) == find(0) { // 能容纳水，且不在闭合区域里面
			ans++
		}
	}
	return ans / 2
}
 Comments
On this page
LCP 71-集水器