LCP 75-传送卷轴

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 17:01:06 2023-09-13 17:01:06 Updated    

随着不断的深入，小扣来到了守护者之森寻找的魔法水晶。首先，他必须先通过守护者的考验。 考验的区域是一个正方形的迷宫，maze[i][j] 表示在迷宫
i 行 j 列的地形： - 若为 . ，表示可以到达的空地； - 若为 # ，表示不可到达的墙壁； - 若为 S
，表示小扣的初始位置； - 若为 T ，表示魔法水晶的位置。 小扣每次可以向 上、下、左、右
相邻的位置移动一格。而守护者拥有一份「传送魔法卷轴」，使用规则如下： - 魔法需要在小扣位于 空地 时才能释放，发动后卷轴消失；； -
发动后，小扣会被传送到水平或者竖直的镜像位置，且目标位置不得为墙壁(如下图所示)；
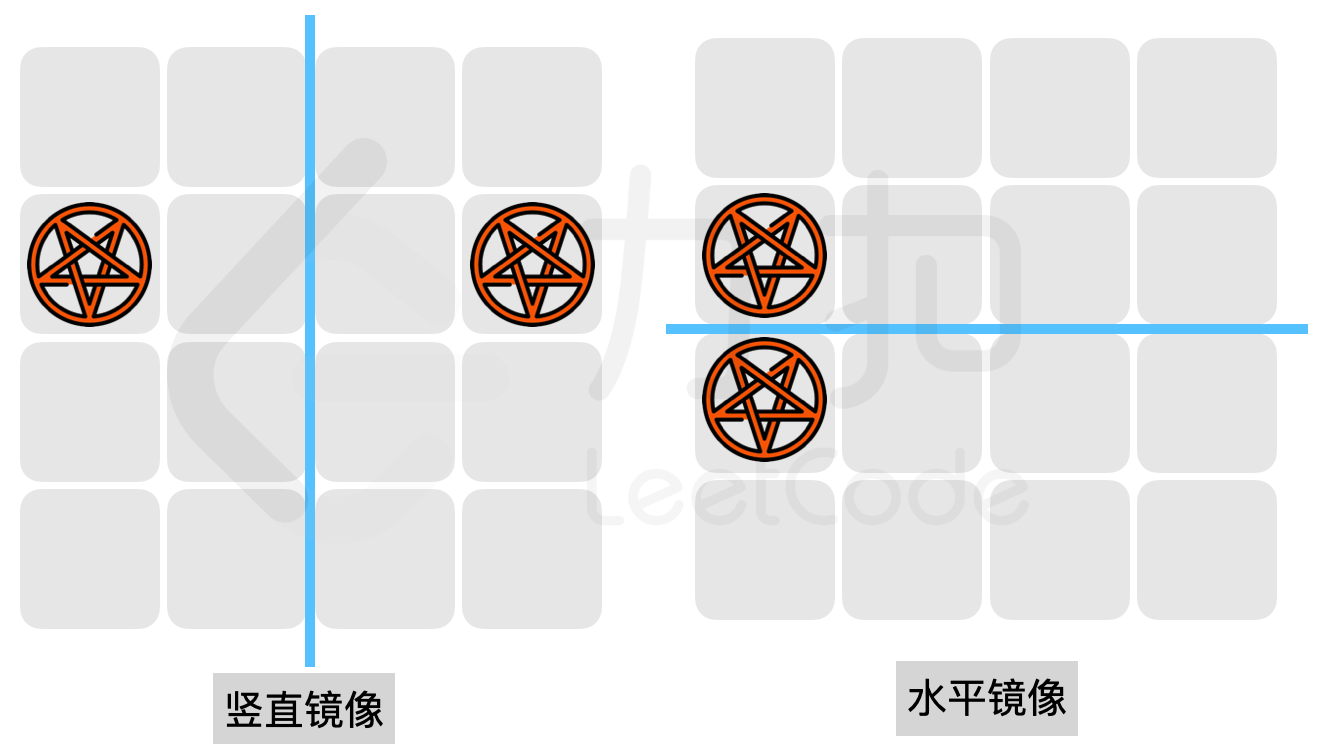![image.png](https://pic.leetcode.cn/1681789509-wTekFu-
image.png){:width=400px}
在使用卷轴后，小扣将被「附加负面效果」，因此小扣需要尽可能缩短传送后到达魔法水晶的距离。而守护者的目标是阻止小扣到达魔法水晶的位置；如果无法阻止，则尽可能
增加 小扣传送后到达魔法水晶的距离。 假设小扣和守护者都按最优策略行事，返回小扣需要在 「附加负面效果」的情况下 最少
移动多少次才能到达魔法水晶。如果无法到达，返回 -1。 注意： - 守护者可以不使用卷轴； - 传送后的镜像位置可能与原位置相同。 示例
1： >输入：maze = [".....","##S..","...#.","T.#..","###.."] > >输出：7 >

解释：如下图所示： >守护者释放魔法的两个最佳的位置为 [2,0] 或 [3,1]： >若小扣经过 [2,0]，守护者在该位置释放魔法， >小扣被传送至
[2,4] 处且加上负面效果，此时小扣还需要移动 7 次才能到达魔法水晶； >若小扣经过 [3,1]，守护者在该位置释放魔法， >小扣被传送至 [3,3]
处且加上负面效果，此时小扣还需要移动 9 次才能到达魔法水晶； >因此小扣负面效果下最少需要移动 7 次才能到达魔法水晶。
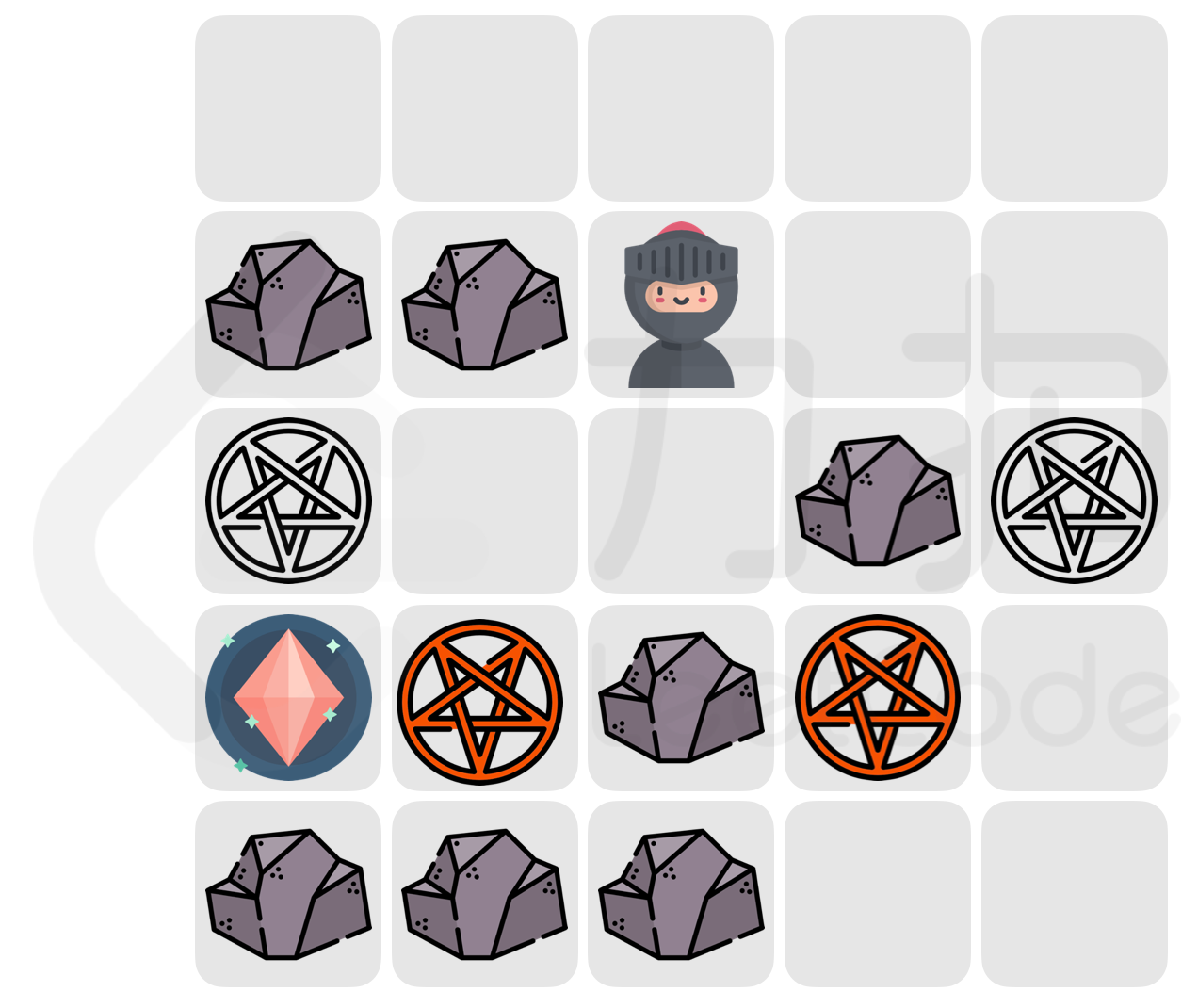![image.png](https://pic.leetcode.cn/1681714676-gksEMT-
image.png){:width=300px} 示例 2： >输入：maze = [".#..","..##",".#S.",".#.T"]

输出：-1 > >解释：如下图所示。 >若小扣向下移动至 [3,2]，守护者使其传送至 [0,2]，小扣将无法到达魔法水晶； >若小扣向右移动至
[2,3]，守护者使其传送至 [2,0]，小扣将无法到达魔法水晶；
![image.png](https://pic.leetcode.cn/1681714693-LsxKAh-
image.png){:width=300px} 示例 3： >输入：maze = ["S###.","..###","#..##","##..#","###.T"] > >输出：5 > >解释：如下图所示：
守护者需要小扣在空地才能释放，因此初始无法将其从 [0,0] 传送至 [0,4]; >当小扣移动至 [2,1] 时，释放卷轴将其传送至水平方向的镜像位置
[2,1]（为原位置） >而后小扣需要移动 5 次到达魔法水晶
![image.png](https://pic.leetcode.cn/1681800985-KrSdru-
image.png){:width=300px} 提示： - 4 <= maze.length == maze[i].length <= 200 - maze[i][j] 仅包含 "."、"#"、"S"、"T"

本题视频讲解

见【力扣杯2023春·个人赛】 第四题。

思路

  1. 遍历，找到 S 和 T 的位置。
  2. BFS，计算 T 到其余点的最短距离。
  3. 如果发现 S 无法到达 T，直接返回 -1。
  4. 二分答案 maxDis：看能否在「附加负面效果」的情况下，移动不超过 maxDis 步到达终点。我写的 DFS，如果 DFS 中的某个位置，守护者使用卷轴传送小扣，并将小扣传送到一个无法到达终点，或者无法在 maxDis 步内到达终点的位置，则不再 DFS（相当于这种位置小扣不能走）。在这种情况下，只要可以到达终点，则说明答案至多为 maxDis，否则说明答案大于 maxDis。

注：如果守护者无法发动传送，则答案为 0。

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class Solution:
    def challengeOfTheKeeper(self, maze: List[str]) -> int:
        m, n = len(maze), len(maze[0])

        # 1. 找到起点终点坐标
        for i, row in enumerate(maze):
            for j, c in enumerate(row):
                if c == 'S':
                    sx, sy = i, j
                elif c == 'T':
                    tx, ty = i, j

        # 2. BFS 计算终点到其余点的最短距离
        dis_from_t = [[inf] * n for _ in range(m)]
        dis_from_t[tx][ty] = 0
        q = [(tx, ty)]
        step = 1
        while q:
            tmp = q
            q = []
            for i, j in tmp:
                for x, y in (i + 1, j), (i - 1, j), (i, j + 1), (i, j - 1):
                    if 0 <= x < m and 0 <= y < n and maze[x][y] != '#' and dis_from_t[x][y] == inf:
                        dis_from_t[x][y] = step
                        q.append((x, y))
            step += 1

        # 3. 剪枝：如果 S 无法到达 T，直接返回 -1
        if dis_from_t[sx][sy] == inf:
            return -1

        # 4. 二分答案 https://www.bilibili.com/video/BV1AP41137w7/
        vis = [[-1] * n for _ in range(m)]
        def check(max_dis: int) -> bool:
            # DFS，看能否在「附加负面效果」的情况下，移动不超过 max_dis 步到达终点
            def dfs(i: int, j: int) -> bool:
                if i < 0 or i >= m or j < 0 or j >= n or vis[i][j] == max_dis or maze[i][j] == '#':
                    return False
                if maze[i][j] == 'T':  # 到达终点
                    return True
                vis[i][j] = max_dis  # 为避免反复创建 vis，用一个每次二分都不一样的数来标记
                # 守护者使用卷轴传送小扣，如果小扣无法在 maxDis 步内到达终点，则返回 false
                if maze[i][j] == '.' and \
                   (maze[i][n - 1 - j] != '#' and dis_from_t[i][n - 1 - j] > max_dis or
                    maze[m - 1 - i][j] != '#' and dis_from_t[m - 1 - i][j] > max_dis):
                    return False
                for x, y in (i + 1, j), (i - 1, j), (i, j + 1), (i, j - 1):
                    if dfs(x, y):
                        return True
                return False
            return dfs(sx, sy)
        ans = bisect_left(range(m * n + 1), True, key=check)
        return -1 if ans > m * n else ans
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
class Solution {
    private final static int[][] DIRS = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };
    private char[][] maze;
    private int[][] disFromT, vis;
    private int sx, sy, maxDis;

    public int challengeOfTheKeeper(String[] Maze) {
        int m = Maze.length, n = Maze[0].length(), tx = 0, ty = 0;
        maze = new char[m][];
        disFromT = new int[m][n];
        // 1. 找到起点终点坐标
        for (int i = 0; i < m; ++i) {
            maze[i] = Maze[i].toCharArray();
            for (int j = 0; j < n; ++j) {
                disFromT[i][j] = Integer.MAX_VALUE;
                if (maze[i][j] == 'S') {
                    sx = i;
                    sy = j;
                } else if (maze[i][j] == 'T') {
                    tx = i;
                    ty = j;
                }
            }
        }

        // 2. BFS 计算终点到其余点的最短距离
        disFromT[tx][ty] = 0;
        var q = new ArrayList<int[]>();
        q.add(new int[]{tx, ty});
        for (int step = 1; !q.isEmpty(); ++step) {
            var tmp = q;
            q = new ArrayList<>();
            for (var p : tmp) {
                for (var d : DIRS) {
                    int x = p[0] + d[0], y = p[1] + d[1];
                    if (0 <= x && x < m && 0 <= y && y < n && maze[x][y] != '#' && disFromT[x][y] == Integer.MAX_VALUE) {
                        disFromT[x][y] = step;
                        q.add(new int[]{x, y});
                    }
                }
            }
        }

        // 3. 剪枝：如果 S 无法到达 T，直接返回 -1
        if (disFromT[sx][sy] == Integer.MAX_VALUE)
            return -1;

        // 4. 二分答案 https://www.bilibili.com/video/BV1AP41137w7/
        vis = new int[m][n];
        int left = -1, right = m * n + 1;
        while (left + 1 < right) {
            maxDis = (left + right) >>> 1;
            if (dfs(sx, sy)) right = maxDis;
            else left = maxDis;
        }
        return right > m * n ? -1 : right;
    }

    private boolean dfs(int x, int y) {
        int m = maze.length, n = maze[0].length;
        if (x < 0 || x >= m || y < 0 || y >= n || vis[x][y] == maxDis + 1 || maze[x][y] == '#')
            return false;
        if (maze[x][y] == 'T') // 到达终点
            return true;
        vis[x][y] = maxDis + 1; // 为避免反复创建 vis，用一个每次二分都不一样的数来标记
        // 守护者使用卷轴传送小扣，如果小扣无法在 maxDis 步内到达终点，则返回 false
        if (maze[x][y] == '.' &&
            (maze[m - x - 1][y] != '#' && disFromT[m - 1 - x][y] > maxDis ||
             maze[x][n - 1 - y] != '#' && disFromT[x][n - 1 - y] > maxDis))
            return false;
        for (var d : DIRS)
            if (dfs(x + d[0], y + d[1]))
                return true;
        return false;
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class Solution {
    static constexpr int dirs[4][2] = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };
public:
    int challengeOfTheKeeper(vector<string> &maze) {
        // 1. 找到起点终点坐标
        int m = maze.size(), n = maze[0].size(), sx, sy, tx, ty, disFromT[m][n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                disFromT[i][j] = INT_MAX;
                if (maze[i][j] == 'S')
                    sx = i, sy = j;
                else if (maze[i][j] == 'T')
                    tx = i, ty = j;
            }
        }

        // 2. BFS 计算终点到其余点的最短距离
        disFromT[tx][ty] = 0;
        vector<pair<int, int>> q = { {tx, ty} };
        for (int step = 1; !q.empty(); ++step) {
            vector<pair<int, int>> nq;
            for (auto &[i, j]: q) {
                for (auto &d: dirs) {
                    int x = i + d[0], y = j + d[1];
                    if (0 <= x && x < m && 0 <= y && y < n && maze[x][y] != '#' && disFromT[x][y] == INT_MAX) {
                        disFromT[x][y] = step;
                        nq.emplace_back(x, y);
                    }
                }
            }
            q = move(nq);
        }

        // 3. 剪枝：如果 S 无法到达 T，直接返回 -1
        if (disFromT[sx][sy] == INT_MAX)
            return -1;

        // 4. 二分答案 https://www.bilibili.com/video/BV1AP41137w7/
        int vis[m][n], maxDis;
        memset(vis, -1, sizeof(vis));
        function<bool(int, int)> dfs = [&](int x, int y) {
            if (x < 0 || x >= m || y < 0 || y >= n || vis[x][y] == maxDis || maze[x][y] == '#')
                return false;
            if (maze[x][y] == 'T') // 到达终点
                return true;
            vis[x][y] = maxDis; // 为避免反复创建 vis，用一个每次二分都不一样的数来标记
            // 守护者使用卷轴传送小扣，如果小扣无法在 maxDis 步内到达终点，则返回 false
            if (maze[x][y] == '.' &&
                (maze[m - x - 1][y] != '#' && disFromT[m - 1 - x][y] > maxDis ||
                 maze[x][n - 1 - y] != '#' && disFromT[x][n - 1 - y] > maxDis))
                return false;
            for (auto &d: dirs)
                if (dfs(x + d[0], y + d[1]))
                    return true;
            return false;
        };
        int left = -1, right = m * n + 1;
        while (left + 1 < right) {
            maxDis = left + (right - left) / 2;
            (dfs(sx, sy) ? right : left) = maxDis;
        }
        return right > m * n ? -1 : right;
    }
};
[sol1-Go]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
type pair struct{ x, y int }
var dirs = []pair{ {-1, 0}, {1, 0}, {0, -1}, {0, 1} }

func challengeOfTheKeeper(maze []string) int {
	m, n := len(maze), len(maze[0])

	// 1. 找到起点终点坐标
	var sx, sy, tx, ty int
	for i, row := range maze {
		for j, c := range row {
			if c == 'S' {
				sx, sy = i, j
			} else if c == 'T' {
				tx, ty = i, j
			}
		}
	}

	// 2. BFS 计算终点到其余点的最短距离
	disFromT := make([][]int, m)
	for i := range disFromT {
		disFromT[i] = make([]int, n)
		for j := range disFromT[i] {
			disFromT[i][j] = math.MaxInt
		}
	}
	disFromT[tx][ty] = 0
	q := []pair{ {tx, ty} }
	for step := 1; len(q) > 0; step++ {
		tmp := q
		q = nil
		for _, p := range tmp {
			for _, d := range dirs {
				x, y := p.x+d.x, p.y+d.y
				if 0 <= x && x < m && 0 <= y && y < n && maze[x][y] != '#' && disFromT[x][y] == math.MaxInt {
					disFromT[x][y] = step
					q = append(q, pair{x, y})
				}
			}
		}
	}

	// 3. 剪枝：如果 S 无法到达 T，直接返回 -1
	if disFromT[sx][sy] == math.MaxInt {
		return -1
	}

	// 4. 二分答案 https://www.bilibili.com/video/BV1AP41137w7/
	vis := make([][]int, m)
	for i := range vis {
		vis[i] = make([]int, n)
	}
	ans := sort.Search(m*n+1, func(maxDis int) bool {
		// DFS，看能否在「附加负面效果」的情况下，移动不超过 maxDis 步到达终点
		var dfs func(int, int) bool
		dfs = func(i, j int) bool {
			if i < 0 || i >= m || j < 0 || j >= n || vis[i][j] == maxDis+1 || maze[i][j] == '#' {
				return false
			}
			if maze[i][j] == 'T' { // 到达终点
				return true
			}
			vis[i][j] = maxDis + 1 // 为避免反复创建 vis，用一个每次二分都不一样的数来标记
			if maze[i][j] == '.' {
				// 守护者使用卷轴传送小扣，如果小扣无法在 maxDis 步内到达终点，则返回 false
				if x, y := i, n-1-j; maze[x][y] != '#' && disFromT[x][y] > maxDis {
					return false
				}
				if x, y := m-1-i, j; maze[x][y] != '#' && disFromT[x][y] > maxDis {
					return false
				}
			}
			// 枚举四个方向
			for _, d := range dirs {
				if dfs(i+d.x, j+d.y) { // 到达终点
					return true
				}
			}
			return false // 无法到达终点
		}
		return dfs(sx, sy)
	})
	if ans > m*n { // 守护者使用卷轴传送小扣，可以把小扣传送到一个无法到达终点的位置
		return -1
	}
	return ans
}

复杂度分析

  • 时间复杂度：\mathcal{O}(mn\log(mn))，其中 m 和 n 分别为 maze 的行数和列数。本题 m=n。
  • 空间复杂度：\mathcal{O}(mn)。

相似题目

 Comments
On this page
LCP 75-传送卷轴
  1. 本题视频讲解
  2. 思路
  3. 复杂度分析
  4. 相似题目