LCP 76-魔法棋盘

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:32 2023-09-13 16:06:32 Updated    

在大小为 n * m 的棋盘中，有两种不同的棋子：黑色，红色。当两颗颜色不同的棋子同时满足以下两种情况时，将会产生魔法共鸣： -
两颗异色棋子在同一行或者同一列 - 两颗异色棋子之间恰好只有一颗棋子 > 注：异色棋子之间可以有空位
由于棋盘上被施加了魔法禁制，棋盘上的部分格子变成问号。chessboard[i][j] 表示棋盘第 i 行 j 列的状态： - 若为 .
，表示当前格子确定为空 - 若为 B ，表示当前格子确定为 黑棋 - 若为 R ，表示当前格子确定为 红棋 - 若为 ?
，表示当前格子待定 现在，探险家小扣的任务是确定所有问号位置的状态（留空/放黑棋/放红棋），使最终的棋盘上，任意两颗棋子间都 无法
产生共鸣。请返回可以满足上述条件的放置方案数量。 示例1： > 输入：n = 3, m = 3, chessboard = ["..R","..B","?R?"] > > 输出：5 > > 解释：给定的棋盘如图：

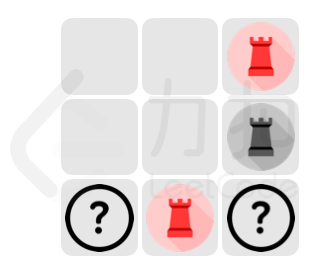![image.png](https://pic.leetcode.cn/1681714583-unbRox-
image.png){:height=150px} > 所有符合题意的最终局面如图：
![image.png](https://pic.leetcode.cn/1681714596-beaOHK-
image.png){:height=150px} 示例2： > 输入：n = 3, m = 3, chessboard = ["?R?","B?B","?R?"] > > 输出：105 提示： - n == chessboard.length - m == chessboard[i].length - 1 <= n*m <= 30 - chessboard 中仅包含
"."、"B"、"R"、"?"

本题视频讲解

见【力扣杯2023春·个人赛】 第五题。

思路

注：题意中的「两颗异色棋子之间恰好只有一颗棋子」允许中间有空格子。

分类讨论，对于一行或者一列的 RB 序列，有以下 7 种情况：

  • 空。
  • 只有一个 B。
  • 只有一个 R。
  • 连续多个 B。
  • 连续多个 R。
  • BR 交替，且以 B 结尾。
  • BR 交替，且以 R 结尾。

为什么单独一个 B/R 也算一个状态？因为既可以变成连续多个 B/R，又可以变成 BR 交替。而「连续多个 B/R」和 「BR 交替」是无法互相转换的。

遍历棋盘的过程就是在不断生成序列的过程，那么向序列末尾添加 B 或者 R，这些状态就会互相转换，形成一个 7\cdot 2 的转换关系表，用数组 trans 记录，其中 -1 表示非法转换。（见代码）

由于有 7 种情况，可以用 3 个比特存储，所有列合并在一起就需要 3m 个比特，这可以用一个二进制数 mask 来存储。

写一个记忆化搜索，DFS}(r,\textit{mask}) 表示枚举到第 r 行，每列的 RB 序列的状态组合起来是 mask 时，继续向后枚举可以得到多少合法的方案。

考虑从下一行的 DFS}(r+1,\textit{mask}’) 转移过来，如何枚举 mask}’ 呢？

写一个暴力搜索来枚举，枚举第 r 行怎么放棋子是合法的。定义 dfs}(c,\textit{rowMask},\textit{colMask}) 表示搜索到第 c 列，当前行的 RB 序列状态是 rowMask，每列的 RB 序列的状态组合起来是 colMask：

  • 如果当前符号是 B，则往当前行和当前列的末尾添加 B，根据 trans 来看是否合法，如果合法就继续搜索。
  • 如果当前符号是 R，则往当前行和当前列的末尾添加 R，根据 trans 来看是否合法，如果合法就继续搜索。
  • 如果当前符号是 ?，则往当前行和当前列的末尾添加 R、添加 B、或者什么也不加，根据 trans 来看是否合法，如果合法就继续搜索。
  • 如果当前符号是 .，继续搜索。
  • c=m 时，表示对于当前行，搜索到一个合法的方案，也就是 mask}’=\textit{colMask，那么可以继续递归 DFS}(r+1,\textit{mask}’)。

当 r=n 时，表示找到了一个合法的方案，返回 1。

递归入口：DFS}(0,0)。

注：代码实现时，如果 n<m 就旋转棋盘，这样可以保证 m\le 5。

其它语言稍后补充。

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
TRANS = (
    # (当前序列末尾添加 B 之后的状态，当前序列末尾添加 R 之后的状态)
    (1, 2),   # 0: 空
    (3, 6),   # 1: 一个 B
    (5, 4),   # 2: 一个 R
    (3, -1),  # 3: 连续多个 B
    (-1, 4),  # 4: 连续多个 R
    (-1, 6),  # 5: BR 交替，且以 B 结尾
    (5, -1),  # 6: BR 交替，且以 R 结尾
)

class Solution:
    def getSchemeCount(self, n: int, m: int, a: List[str]) -> int:
        if n < m:  # 保证 n >= m
            a = [list(col) for col in zip(*a)]
            n, m = m, n
        @cache
        def DFS(r: int, mask: int) -> int:
            if r == n:
                return 1
            # 写一个爆搜，生成出所有的合法状态
            def dfs(c: int, row_mask: int, col_mask: int) -> int:
                if c == m:
                    return DFS(r + 1, col_mask)  # 枚举下一行
                def nxt(color: int) -> int:
                    rm = TRANS[row_mask][color]  # 新的 rowMask
                    if rm < 0: return 0  # 非法
                    c3 = c * 3
                    cm = TRANS[(col_mask >> c3) & 7][color]  # 新的 colMask 的第 c 列
                    if cm < 0: return 0 # 非法
                    cm = col_mask & ~(7 << c3) | (cm << c3)  # 修改 colMask 的第 c 列
                    return dfs(c + 1, rm, cm)
                b = a[r][c]
                if b == 'B':
                    return nxt(0)
                if b == 'R':
                    return nxt(1)
                if b == '.':
                    return dfs(c + 1, row_mask, col_mask)
                return dfs(c + 1, row_mask, col_mask) + nxt(0) + nxt(1)
            return dfs(0, 0, mask)
        return DFS(0, 0)
[sol1-Go]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
// 每一行的含义：{当前序列末尾添加 B 后的状态，当前序列末尾添加 R 后的状态}
var trans = [7][2]int{
	{1, 2},  // 空
	{3, 6},  // 只有一个 B
	{5, 4},  // 只有一个 R
	{3, -1}, // 连续多个 B
	{-1, 4}, // 连续多个 R
	{-1, 6}, // BR 交替，且以 B 结尾
	{5, -1}, // BR 交替，且以 R 结尾
}

func getSchemeCount(n, m int, g []string) int64 {
	a := make([][]byte, n)
	for i, row := range g {
		a[i] = []byte(row)
	}
	if n < m {
		a = rotate(a) // 保证 n >= m
		n, m = m, n
	}

	memo := make([][]int, n)
	for i := range memo {
		memo[i] = make([]int, 1<<(m*3))
		for j := range memo[i] {
			memo[i][j] = -1
		}
	}
	var DFS func(int, int) int
	DFS = func(r, mask int) int {
		if r == n { // 找到 1 个合法方案
			return 1
		}
		ptr := &memo[r][mask]
		if *ptr != -1 {
			return *ptr
		}
		// 写一个爆搜，生成所有的合法状态
		var dfs func(int, int, int) int
		dfs = func(c, rowMask, colMask int) (res int) {
			if c == m {
				return DFS(r+1, colMask) // 枚举下一行
			}
			next := func(color int) int {
				rm := trans[rowMask][color] // 新的 rowMask
				if rm < 0 { // 非法
					return 0
				}
				c3 := c * 3
				cm := trans[colMask>>c3&7][color] // 新的 colMask 的第 c 列
				if cm < 0 { // 非法
					return 0
				}
				return dfs(c+1, rm, colMask&^(7<<c3)|cm<<c3) // 修改 colMask 的第 c 列
			}
			switch a[r][c] {
			case 'B': // 填 B
				return next(0)
			case 'R': // 填 R
				return next(1)
			case '?': // 留空 / 填 B / 填 R
				return dfs(c+1, rowMask, colMask) + next(0) + next(1)
			default: // 留空
				return dfs(c+1, rowMask, colMask)
			}
		}
		*ptr = dfs(0, 0, mask)
		return *ptr
	}
	return int64(DFS(0, 0))
}

func rotate(a [][]byte) [][]byte {
	n, m := len(a), len(a[0])
	b := make([][]byte, m)
	for i := range b {
		b[i] = make([]byte, n)
	}
	for i, r := range a {
		for j, v := range r {
			b[j][n-1-i] = v
		}
	}
	return b
}

复杂度分析

  • 时间复杂度：\mathcal{O}(n21^{m})。这里保证 m\le 5\le \sqrt{nm（如果 n<m 则旋转棋盘）。动态规划的时间复杂度 = 状态个数 \times 单个状态的计算时间。这里状态个数为 \mathcal{O}(n7^{m})，单个状态的计算时间为 \mathcal{O}(3^{m})，因此时间复杂度为 \mathcal{O}(n7^{m}3^{m})=\mathcal{O}(n21^{m})。考虑到很多状态是非法的，在全为 ? 的情况下，dfs 最多调用 5601518 次。
  • 空间复杂度：\mathcal{O}(n8^{m})。为了方便用位运算，实际用了 \mathcal{O}(n8^{m}) 的空间来存储状态。
 Comments
On this page
LCP 76-魔法棋盘
  1. 本题视频讲解
  2. 思路
  3. 复杂度分析