LCP 80-生物进化录
在永恒之森中,存在着一本生物进化录,以 一个树形结构 记载了所有生物的演化过程。经过观察并整理了各节点间的关系,parents[i] 表示编号i 节点的父节点编号(根节点的父节点为 -1)。
为了探索和记录其中的演化规律,队伍中的炼金术师提出了一种方法,可以以字符串的形式将其复刻下来,规则如下: - 初始只有一个根节点,表示演化的起点,依次记录01 字符串中的字符, - 如果记录 0,则在当前节点下添加一个子节点,并将指针指向新添加的子节点; - 如果记录1,则将指针回退到当前节点的父节点处。 现在需要应用上述的记录方法,复刻下它的演化过程。请返回能够复刻演化过程的字符串中, 字典序最小 的01 字符串。 注意: - 节点指针最终可以停在任何节点上,不一定要回到根节点。 示例 1: > 输入:parents = [-1,0,0,2] > > 输出:"00110" > >解释:树结构如下图所示,共存在 2 种记录方案: >第 1 种方案为:0(记录编号 1
的节点) -> 1(回退至节点 0) -> 0(记录编号 2 的节点) -> 0((记录编号 3 的节点)) >第 2 种方案为:0(记录编号 2 的节点)
-> 0(记录编号 3 的节点) -> 1(回退至节点 2) -> 1(回退至节点 0) -> 0(记录编号 1 的节点) >返回字典序更小的"00110" 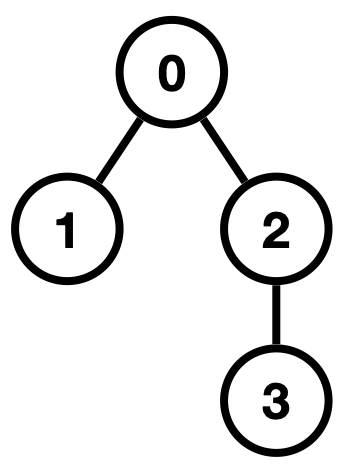{:width=120px}.gif) {:width=320px}
{:width=320px}
示例 2: > 输入:parents = [-1,0,0,1,2,2] > > 输出:"00101100" 提示: - 1 <= parents.length <= 10^4 - -1 <= parents[i] < i (即父节点编号小于子节点)
本题视频讲解
见【力扣杯2023春·战队赛】 第四题。
思路
- 要使整棵树对应的字符串的字典序最小,对于根节点下面的子树,对应的字符串的字典序也要最小,这意味着可以递归处理。
- 如何得到最小字典序?把所有子树的结果排序,然后拼接起来,在开头加上 0,末尾加上 1,然后返回。
- 题目说「节点指针最终可以停在任何节点上,不一定要回到根节点」。我们可以把结果的末尾的 1 都去掉来实现这一点(开头的一个 0 也要去掉)。但这样的话,我们对字符串排序的做法是否会影响答案的正确性呢?
- 假设有两棵子树 A 和 B,先 A 后 B 的结果是 000\cdots 11,先 B 后 A 的结果(字典序更大)是 001\cdots 0\cdots 11,注意中间有个 0,因为无论按照何种顺序遍历 A 和 B,0 和 1 的总数是不变的。所以原来字典序最小的,去掉末尾的 1,字典序仍然是最小的。
- 因此按照上面第 2 点说的,递归实现就好了。
1 | class Solution: |
1 | func evolutionaryRecord(parents []int) string { |
复杂度分析
- 时间复杂度:\mathcal{O}(n^2),其中 n 为 parents 的长度。瓶颈在拼接字符串上(可以用链表等结构优化),对于排序的时间复杂度,感性理解,如果树高比较小,那么比较的字符串就比较短,如果树高比较大,那么参与比较的字符串就比较少。具体分析 。
- 空间复杂度:\mathcal{O}(n)。