LCR 023-相交链表

给定两个单链表的头节点 headA 和 headB ，请找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交 ：

[![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2018/12/14/160_statement.png)](https://assets.leetcode-
cn.com/aliyun-lc-upload/uploads/2018/12/14/160_statement.png)

题目数据 保证 整个链式结构中不存在环。

注意 ，函数返回结果后，链表必须 保持其原始结构 。

示例 1：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2018/12/14/160_example_1.png)

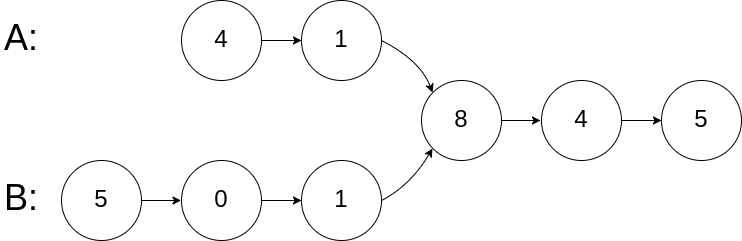
**输入：** intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
**输出：** Intersected at '8'
**解释：** 相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

示例 2：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2018/12/14/160_example_2.png)

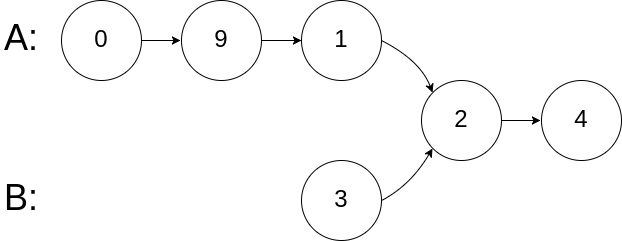
**输入：** intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
**输出：** Intersected at '2'
**解释：** 相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2018/12/14/160_example_3.png)

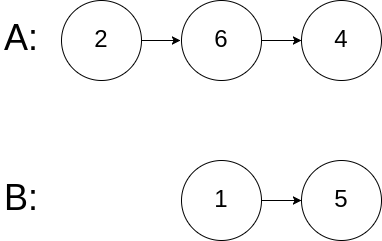
**输入：** intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
**输出：** null
**解释：** 从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

提示：

• listA 中节点数目为 m
• listB 中节点数目为 n
• 0 <= m, n <= 3 * 104
• 1 <= Node.val <= 105
• 0 <= skipA <= m
• 0 <= skipB <= n
• 如果 listA 和 listB 没有交点，intersectVal 为 0
• 如果 listA 和 listB 有交点，intersectVal == listA[skipA + 1] == listB[skipB + 1]

进阶： 能否设计一个时间复杂度 O(n) 、仅用 O(1) 内存的解决方案？

注意：本题与主站 160 题相同：<https://leetcode-cn.com/problems/intersection-of-two-linked-
lists/>

方法一：哈希集合

思路和算法

判断两个链表是否相交，可以使用哈希集合存储链表节点。

首先遍历链表 headA，并将链表 headA 中的每个节点加入哈希集合中。然后遍历链表 headB，对于遍历到的每个节点，判断该节点是否在哈希集合中：

• 如果当前节点不在哈希集合中，则继续遍历下一个节点；

• 如果当前节点在哈希集合中，则后面的节点都在哈希集合中，即从当前节点开始的所有节点都在两个链表的相交部分，因此在链表 headB 中遍历到的第一个在哈希集合中的节点就是两个链表相交的节点，返回该节点。

如果链表 headB 中的所有节点都不在哈希集合中，则两个链表不相交，返回 null。

代码

[sol1-Java]

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        Set<ListNode> visited = new HashSet<ListNode>();
        ListNode temp = headA;
        while (temp != null) {
            visited.add(temp);
            temp = temp.next;
        }
        temp = headB;
        while (temp != null) {
            if (visited.contains(temp)) {
                return temp;
            }
            temp = temp.next;
        }
        return null;
    }
}

[sol1-C#]

public class Solution {
    public ListNode GetIntersectionNode(ListNode headA, ListNode headB) {
        ISet<ListNode> visited = new HashSet<ListNode>();
        ListNode temp = headA;
        while (temp != null) {
            visited.Add(temp);
            temp = temp.next;
        }
        temp = headB;
        while (temp != null) {
            if (visited.Contains(temp)) {
                return temp;
            }
            temp = temp.next;
        }
        return null;
    }
}

[sol1-JavaScript]

var getIntersectionNode = function(headA, headB) {
    const visited = new Set();
    let temp = headA;
    while (temp !== null) {
        visited.add(temp);
        temp = temp.next;
    }
    temp = headB;
    while (temp !== null) {
        if (visited.has(temp)) {
            return temp;
        }
        temp = temp.next;
    }
    return null;
};

[sol1-Golang]

func getIntersectionNode(headA, headB *ListNode) *ListNode {
    vis := map[*ListNode]bool{}
    for tmp := headA; tmp != nil; tmp = tmp.Next {
        vis[tmp] = true
    }
    for tmp := headB; tmp != nil; tmp = tmp.Next {
        if vis[tmp] {
            return tmp
        }
    }
    return nil
}

[sol1-C++]

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        unordered_set<ListNode *> visited;
        ListNode *temp = headA;
        while (temp != nullptr) {
            visited.insert(temp);
            temp = temp->next;
        }
        temp = headB;
        while (temp != nullptr) {
            if (visited.count(temp)) {
                return temp;
            }
            temp = temp->next;
        }
        return nullptr;
    }
};

[sol1-C]

struct HashTable {
    struct ListNode *key;
    UT_hash_handle hh;
};

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    struct HashTable *hashTable = NULL;
    struct ListNode *temp = headA;
    while (temp != NULL) {
        struct HashTable *tmp;
        HASH_FIND(hh, hashTable, &temp, sizeof(struct HashTable *), tmp);
        if (tmp == NULL) {
            tmp = malloc(sizeof(struct HashTable));
            tmp->key = temp;
            HASH_ADD(hh, hashTable, key, sizeof(struct HashTable *), tmp);
        }
        temp = temp->next;
    }
    temp = headB;
    while (temp != NULL) {
        struct HashTable *tmp;
        HASH_FIND(hh, hashTable, &temp, sizeof(struct HashTable *), tmp);
        if (tmp != NULL) {
            return temp;
        }
        temp = temp->next;
    }
    return NULL;
}

复杂度分析

• 时间复杂度：O(m+n)，其中 m 和 n 是分别是链表 headA 和 headB 的长度。需要遍历两个链表各一次。

• 空间复杂度：O(m)，其中 m 是链表 headA 的长度。需要使用哈希集合存储链表 headA 中的全部节点。

方法二：双指针

思路和算法

使用双指针的方法，可以将空间复杂度降至 O(1)。

只有当链表 headA 和 headB 都不为空时，两个链表才可能相交。因此首先判断链表 headA 和 headB 是否为空，如果其中至少有一个链表为空，则两个链表一定不相交，返回 null。

当链表 headA 和 headB 都不为空时，创建两个指针 pA 和 pB，初始时分别指向两个链表的头节点 headA 和 headB，然后将两个指针依次遍历两个链表的每个节点。具体做法如下：

• 每步操作需要同时更新指针 pA 和 pB。

• 如果指针 pA 不为空，则将指针 pA 移到下一个节点；如果指针 pB 不为空，则将指针 pB 移到下一个节点。

• 如果指针 pA 为空，则将指针 pA 移到链表 headB 的头节点；如果指针 pB 为空，则将指针 pB 移到链表 headA 的头节点。

• 当指针 pA 和 pB 指向同一个节点或者都为空时，返回它们指向的节点或者 null。

证明

下面提供双指针方法的正确性证明。考虑两种情况，第一种情况是两个链表相交，第二种情况是两个链表不相交。

情况一：两个链表相交

链表 headA 和 headB 的长度分别是 m 和 n。假设链表 headA 的不相交部分有 a 个节点，链表 headB 的不相交部分有 b 个节点，两个链表相交的部分有 c 个节点，则有 a+c=m，b+c=n。

• 如果 a=b，则两个指针会同时到达两个链表相交的节点，此时返回相交的节点；

• 如果 a \ne b，则指针 pA 会遍历完链表 headA，指针 pB 会遍历完链表 headB，两个指针不会同时到达链表的尾节点，然后指针 pA 移到链表 headB 的头节点，指针 pB 移到链表 headA 的头节点，然后两个指针继续移动，在指针 pA 移动了 a+c+b 次、指针 pB 移动了 b+c+a 次之后，两个指针会同时到达两个链表相交的节点，该节点也是两个指针第一次同时指向的节点，此时返回相交的节点。

情况二：两个链表不相交

链表 headA 和 headB 的长度分别是 m 和 n。考虑当 m=n 和 m \ne n 时，两个指针分别会如何移动：

• 如果 m=n，则两个指针会同时到达两个链表的尾节点，然后同时变成空值 null，此时返回 null；

• 如果 m \ne n，则由于两个链表没有公共节点，两个指针也不会同时到达两个链表的尾节点，因此两个指针都会遍历完两个链表，在指针 pA 移动了 m+n 次、指针 pB 移动了 n+m 次之后，两个指针会同时变成空值 null，此时返回 null。

代码

[sol2-Java]

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) {
            return null;
        }
        ListNode pA = headA, pB = headB;
        while (pA != pB) {
            pA = pA == null ? headB : pA.next;
            pB = pB == null ? headA : pB.next;
        }
        return pA;
    }
}

[sol2-C#]

public class Solution {
    public ListNode GetIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) {
            return null;
        }
        ListNode pA = headA, pB = headB;
        while (pA != pB) {
            pA = pA == null ? headB : pA.next;
            pB = pB == null ? headA : pB.next;
        }
        return pA;
    }
}

[sol2-JavaScript]

var getIntersectionNode = function(headA, headB) {
    if (headA === null || headB === null) {
        return null;
    }
    let pA = headA, pB = headB;
    while (pA !== pB) {
        pA = pA === null ? headB : pA.next;
        pB = pB === null ? headA : pB.next;
    }
    return pA;
};

[sol2-Golang]

func getIntersectionNode(headA, headB *ListNode) *ListNode {
    if headA == nil || headB == nil {
        return nil
    }
    pa, pb := headA, headB
    for pa != pb {
        if pa == nil {
            pa = headB
        } else {
            pa = pa.Next
        }
        if pb == nil {
            pb = headA
        } else {
            pb = pb.Next
        }
    }
    return pa
}

[sol2-C++]

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if (headA == nullptr || headB == nullptr) {
            return nullptr;
        }
        ListNode *pA = headA, *pB = headB;
        while (pA != pB) {
            pA = pA == nullptr ? headB : pA->next;
            pB = pB == nullptr ? headA : pB->next;
        }
        return pA;
    }
};

[sol2-C]

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    if (headA == NULL || headB == NULL) {
        return NULL;
    }
    struct ListNode *pA = headA, *pB = headB;
    while (pA != pB) {
        pA = pA == NULL ? headB : pA->next;
        pB = pB == NULL ? headA : pB->next;
    }
    return pA;
}

复杂度分析

• 时间复杂度：O(m+n)，其中 m 和 n 是分别是链表 headA 和 headB 的长度。两个指针同时遍历两个链表，每个指针遍历两个链表各一次。

• 空间复杂度：O(1)。