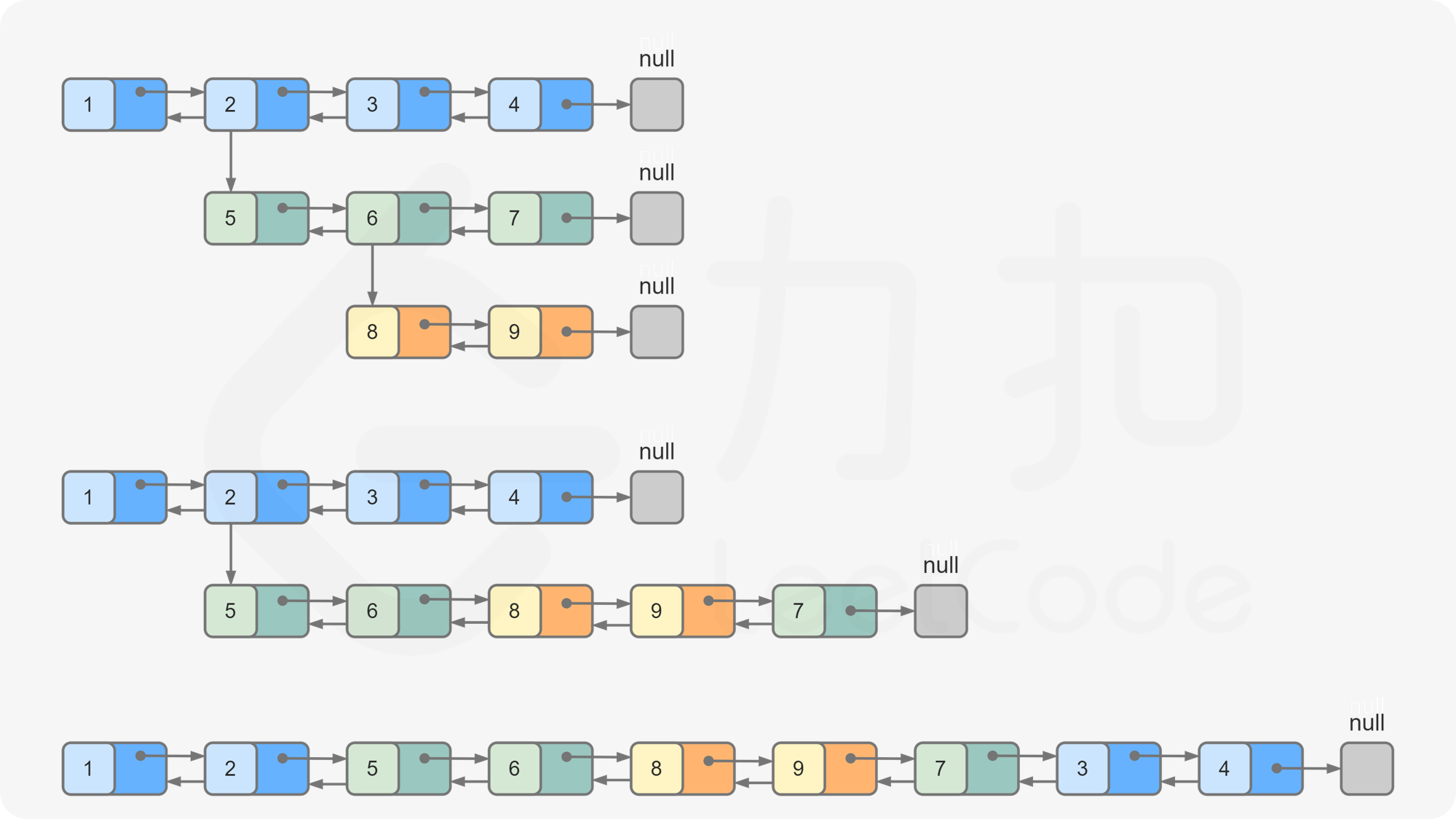
多级双向链表中,除了指向下一个节点和前一个节点指针之外,它还有一个子链表指针,可能指向单独的双向链表。这些子列表也可能会有一个或多个自己的子项,依此类推,生成多级数据结构,如下面的示例所示。
给定位于列表第一级的头节点,请扁平化列表,即将这样的多级双向链表展平成普通的双向链表,使所有结点出现在单级双链表中。
示例 1:
**输入:** head = [1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12]
**输出:** [1,2,3,7,8,11,12,9,10,4,5,6]
**解释:**
输入的多级列表如下图所示:
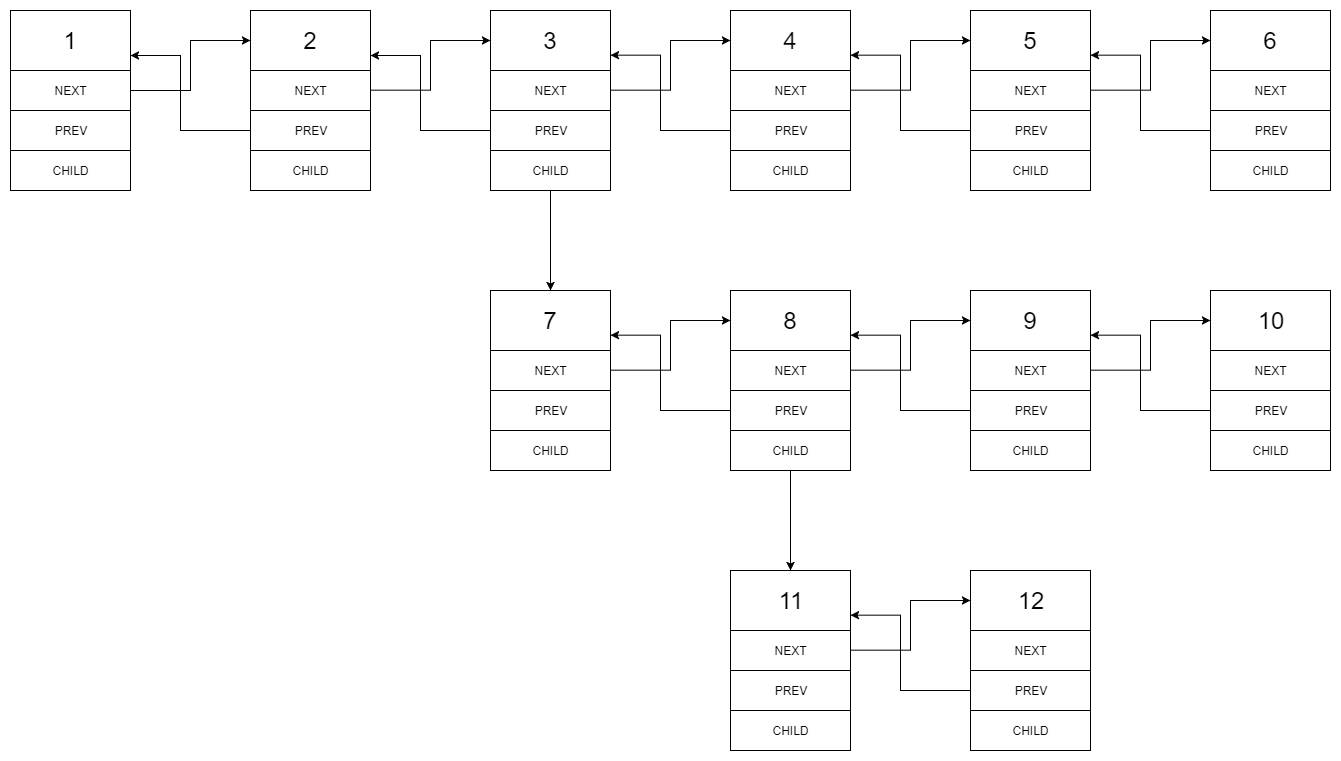
扁平化后的链表如下图:

示例 2:
**输入:** head = [1,2,null,3]
**输出:** [1,3,2]
**解释:** 输入的多级列表如下图所示:
1---2---NULL
|
3---NULL
示例 3:
**输入:** head = []
**输出:** []
如何表示测试用例中的多级链表?
以 示例 1 为例:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
序列化其中的每一级之后:
[1,2,3,4,5,6,null]
[7,8,9,10,null]
[11,12,null]
为了将每一级都序列化到一起,我们需要每一级中添加值为 null 的元素,以表示没有节点连接到上一级的上级节点。
[1,2,3,4,5,6,null]
[null,null,7,8,9,10,null]
[null,11,12,null]
合并所有序列化结果,并去除末尾的 null 。
[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12]
提示:
- 节点数目不超过
1000
1 <= Node.val <= 10^5
注意:本题与主站 430 题相同: <https://leetcode-cn.com/problems/flatten-a-multilevel-
doubly-linked-list/>
方法一:深度优先搜索
思路与算法
当我们遍历到某个节点 node 时,如果它的 child 成员不为空,那么我们需要将 child 指向的链表结构进行扁平化,并且插入 node 与 node 的下一个节点之间。
因此,我们在遇到 child 成员不为空的节点时,就要先去处理 child 指向的链表结构,这就是一个「深度优先搜索」的过程。当我们完成了对 child 指向的链表结构的扁平化之后,就可以「回溯」到 node 节点。
为了能够将扁平化的链表插入 node 与 node 的下一个节点之间,我们需要知道扁平化的链表的最后一个节点 last,随后进行如下的三步操作:
这样一来,我们就可以将扁平化的链表成功地插入。

在深度优先搜索完成后,我们返回给定的首节点即可。
细节
需要注意的是,node 可能没有下一个节点,即 next 为空。此时,我们只需进行第二步操作。
此外,在插入扁平化的链表后,我们需要将 node 的 child 成员置为空。
代码
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
public:
Node* flatten(Node* head) {
function<Node*(Node*)> dfs = [&](Node* node) {
Node* cur = node;
Node* last = nullptr;
while (cur) {
Node* next = cur->next;
if (cur->child) {
Node* child_last = dfs(cur->child);
next = cur->next;
cur->next = cur->child;
cur->child->prev = cur;
if (next) {
child_last->next = next;
next->prev = child_last;
}
cur->child = nullptr;
last = child_last;
}
else {
last = cur;
}
cur = next;
}
return last;
};
dfs(head);
return head;
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
public Node flatten(Node head) {
dfs(head);
return head;
}
public Node dfs(Node node) {
Node cur = node;
Node last = null;
while (cur != null) {
Node next = cur.next;
if (cur.child != null) {
Node childLast = dfs(cur.child);
next = cur.next;
cur.next = cur.child;
cur.child.prev = cur;
if (next != null) {
childLast.next = next;
next.prev = childLast;
}
cur.child = null;
last = childLast;
} else {
last = cur;
}
cur = next;
}
return last;
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| public class Solution {
public Node Flatten(Node head) {
DFS(head);
return head;
}
public Node DFS(Node node) {
Node cur = node;
Node last = null;
while (cur != null) {
Node next = cur.next;
if (cur.child != null) {
Node childLast = DFS(cur.child);
next = cur.next;
cur.next = cur.child;
cur.child.prev = cur;
if (next != null) {
childLast.next = next;
next.prev = childLast;
}
cur.child = null;
last = childLast;
} else {
last = cur;
}
cur = next;
}
return last;
}
}
|
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Solution:
def flatten(self, head: "Node") -> "Node":
def dfs(node: "Node") -> "Node":
cur = node
last = None
while cur:
nxt = cur.next
if cur.child:
child_last = dfs(cur.child)
nxt = cur.next
cur.next = cur.child
cur.child.prev = cur
if nxt:
child_last.next = nxt
nxt.prev = child_last
cur.child = None
last = child_last
else:
last = cur
cur = nxt
return last
dfs(head)
return head
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| var flatten = function(head) {
const dfs = (node) => {
let cur = node;
let last = null;
while (cur) {
let next = cur.next;
if (cur.child) {
const childLast = dfs(cur.child);
next = cur.next;
cur.next = cur.child;
cur.child.prev = cur;
if (next != null) {
childLast.next = next;
next.prev = childLast;
}
cur.child = null;
last = childLast;
} else {
last = cur;
}
cur = next;
}
return last;
}
dfs(head);
return head;
};
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| func dfs(node *Node) (last *Node) {
cur := node
for cur != nil {
next := cur.Next
if cur.Child != nil {
childLast := dfs(cur.Child)
next = cur.Next
cur.Next = cur.Child
cur.Child.Prev = cur
if next != nil {
childLast.Next = next
next.Prev = childLast
}
cur.Child = nil
last = childLast
} else {
last = cur
}
cur = next
}
return
}
func flatten(root *Node) *Node {
dfs(root)
return root
}
|
复杂度分析