LCR 036-逆波兰表达式求值

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:45:43 2023-09-13 16:45:43 Updated    

根据
逆波兰表示法，求该后缀表达式的计算结果。

有效的算符包括 +、-、*、/ 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

说明：

  • 整数除法只保留整数部分。
  • 给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：

**输入：** tokens = ["2","1","+","3","*"]
**输出：** 9
**解释：** 该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

**输入：** tokens = ["4","13","5","/","+"]
**输出：** 6
**解释：** 该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

**输入：** tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
**输出：** 22
**解释：**
该算式转化为常见的中缀算术表达式为：
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
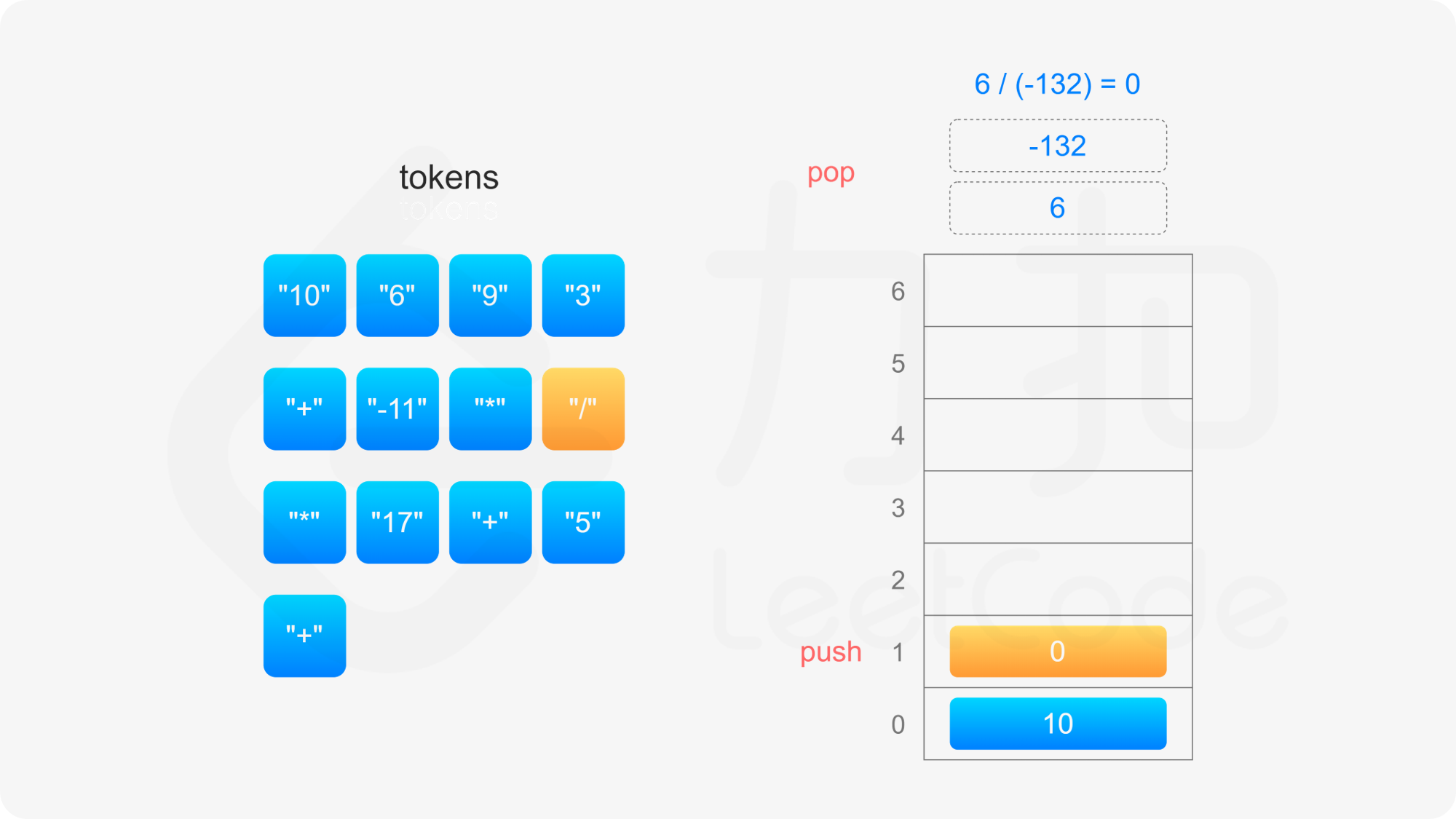
= ((10 * (6 / -132)) + 17) + 5
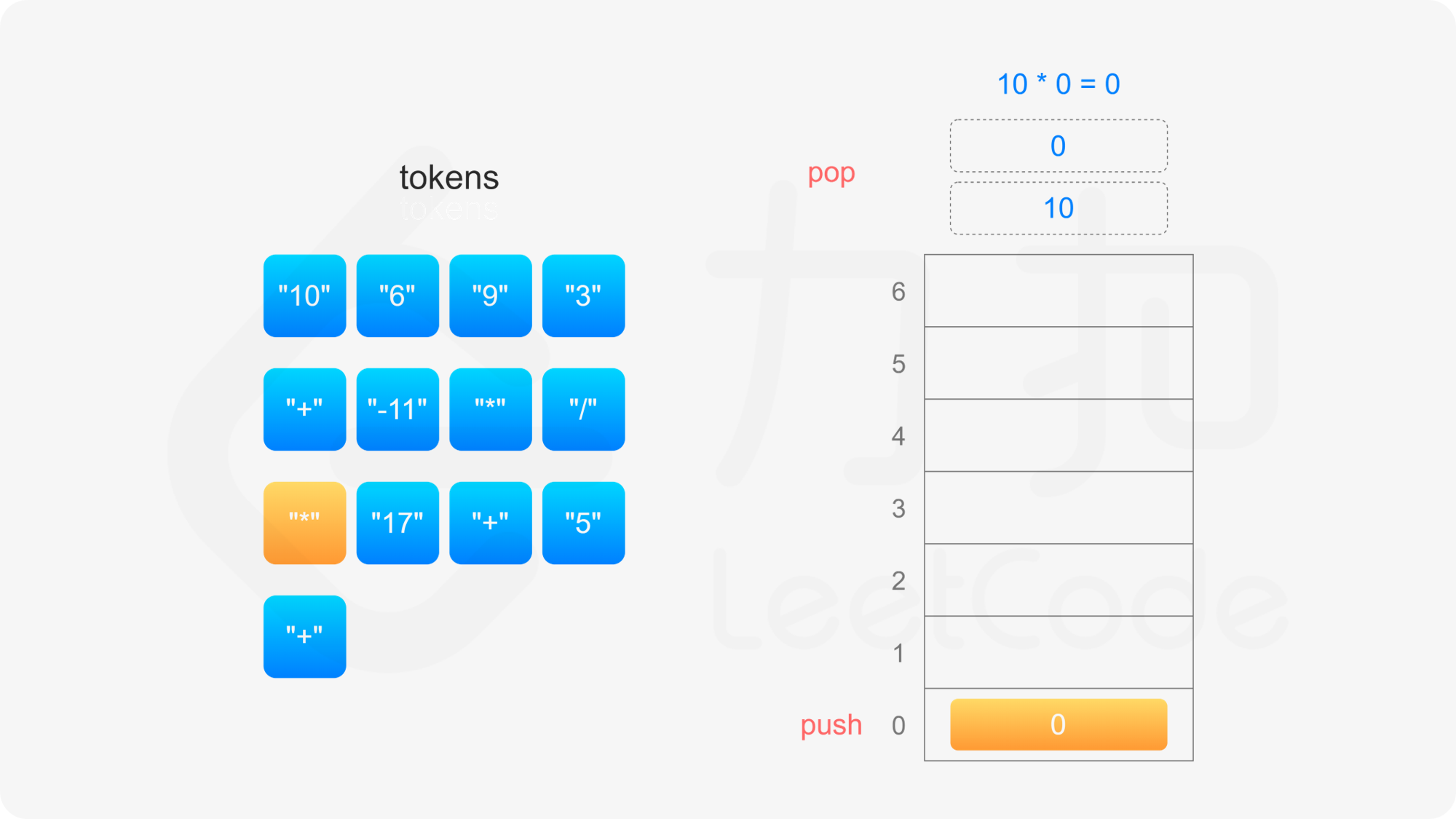
= ((10 * 0) + 17) + 5
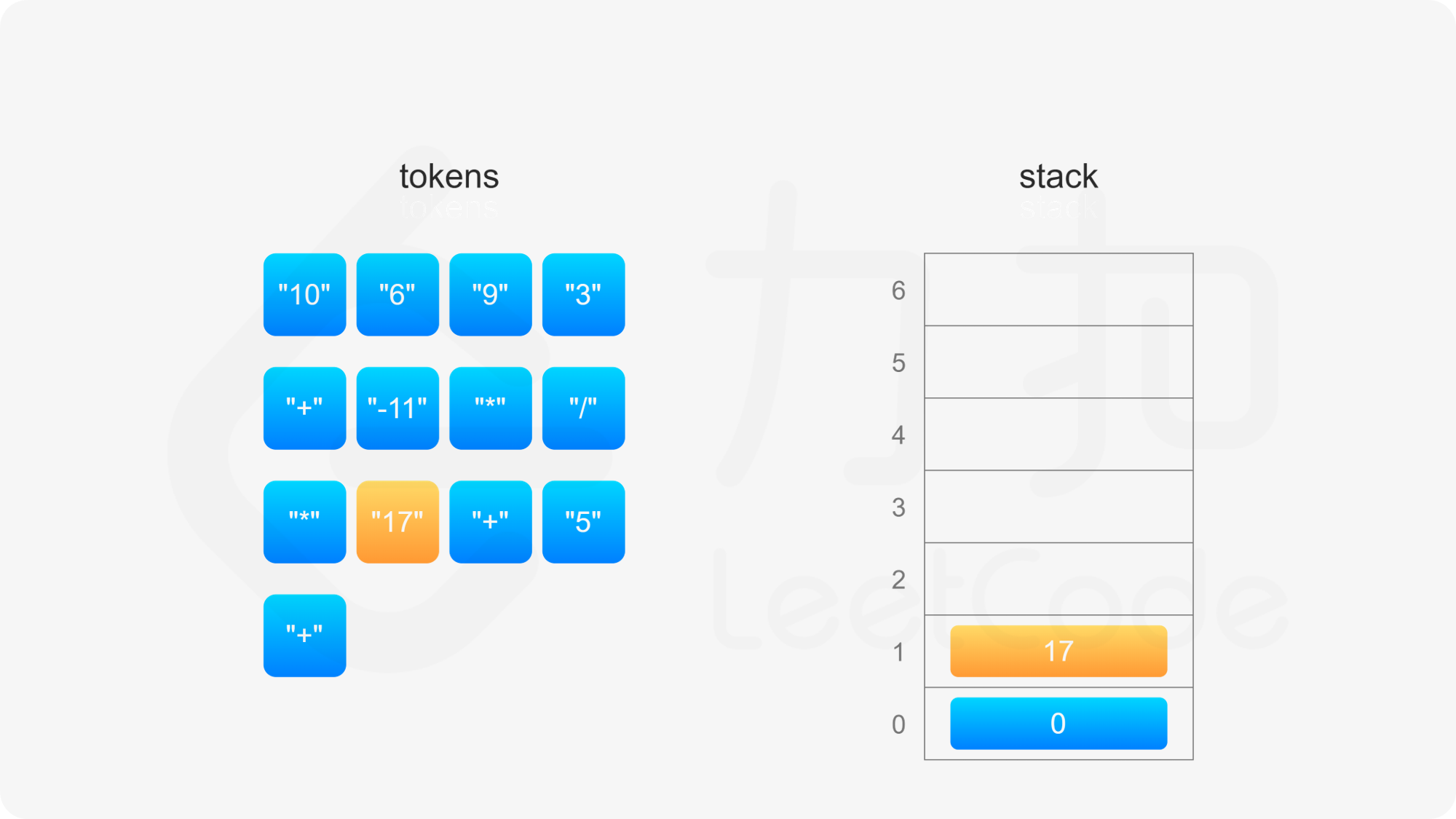
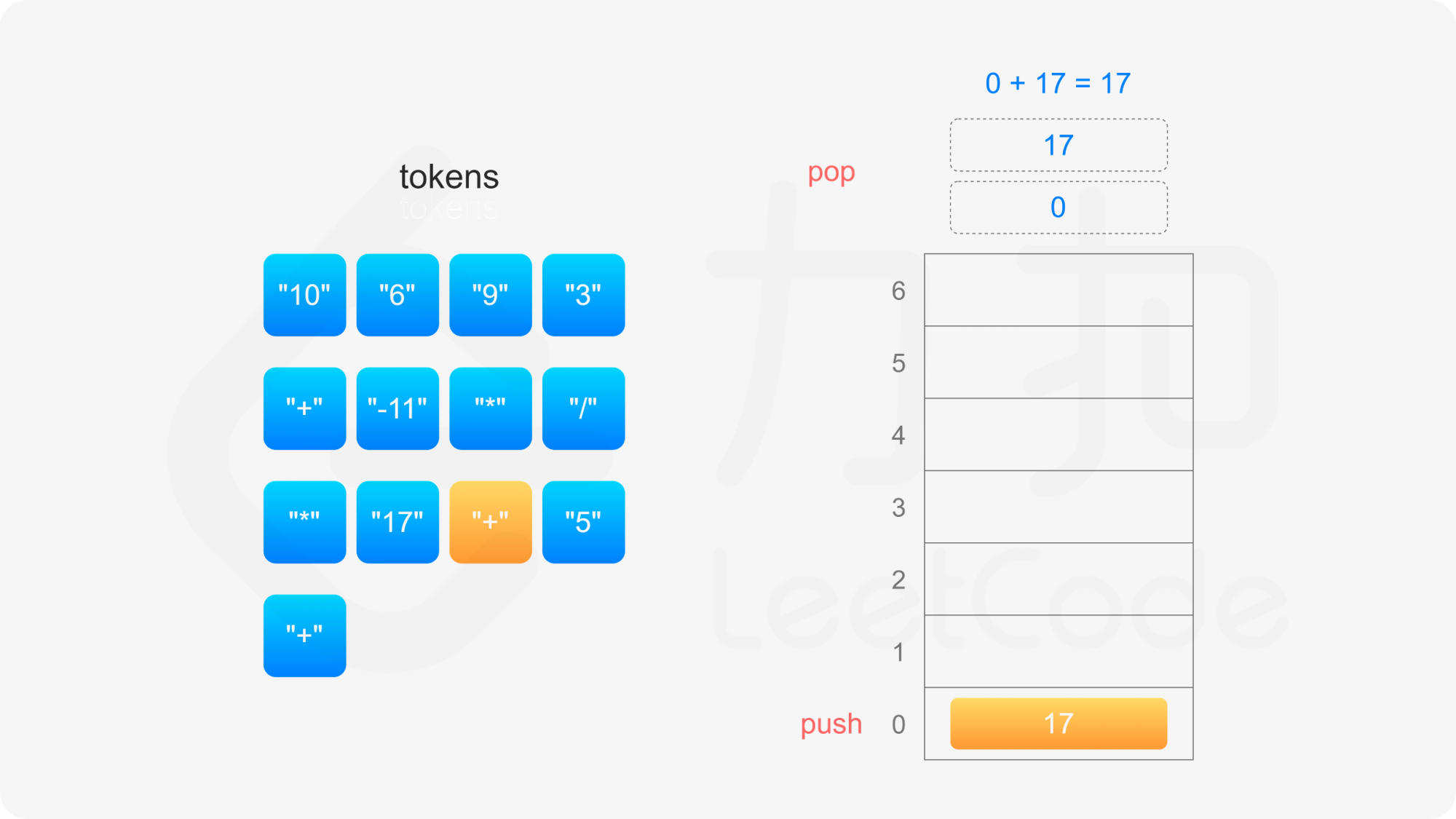
= (0 + 17) + 5
= 17 + 5
= 22

提示：

  • 1 <= tokens.length <= 104
  • tokens[i] 要么是一个算符（"+"、"-"、"*" 或 "/"），要么是一个在范围 [-200, 200] 内的整数

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

  • 平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
  • 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

  • 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
  • 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中。

注意：本题与主站 150 题相同： <https://leetcode-cn.com/problems/evaluate-reverse-polish-
notation/>

前言

后缀表达式由波兰的逻辑学家卢卡西维兹提出，也称逆波兰表达式。后缀表达式的特点是：没有括号，运算符总是放在和它相关的操作数之后。

方法一：栈

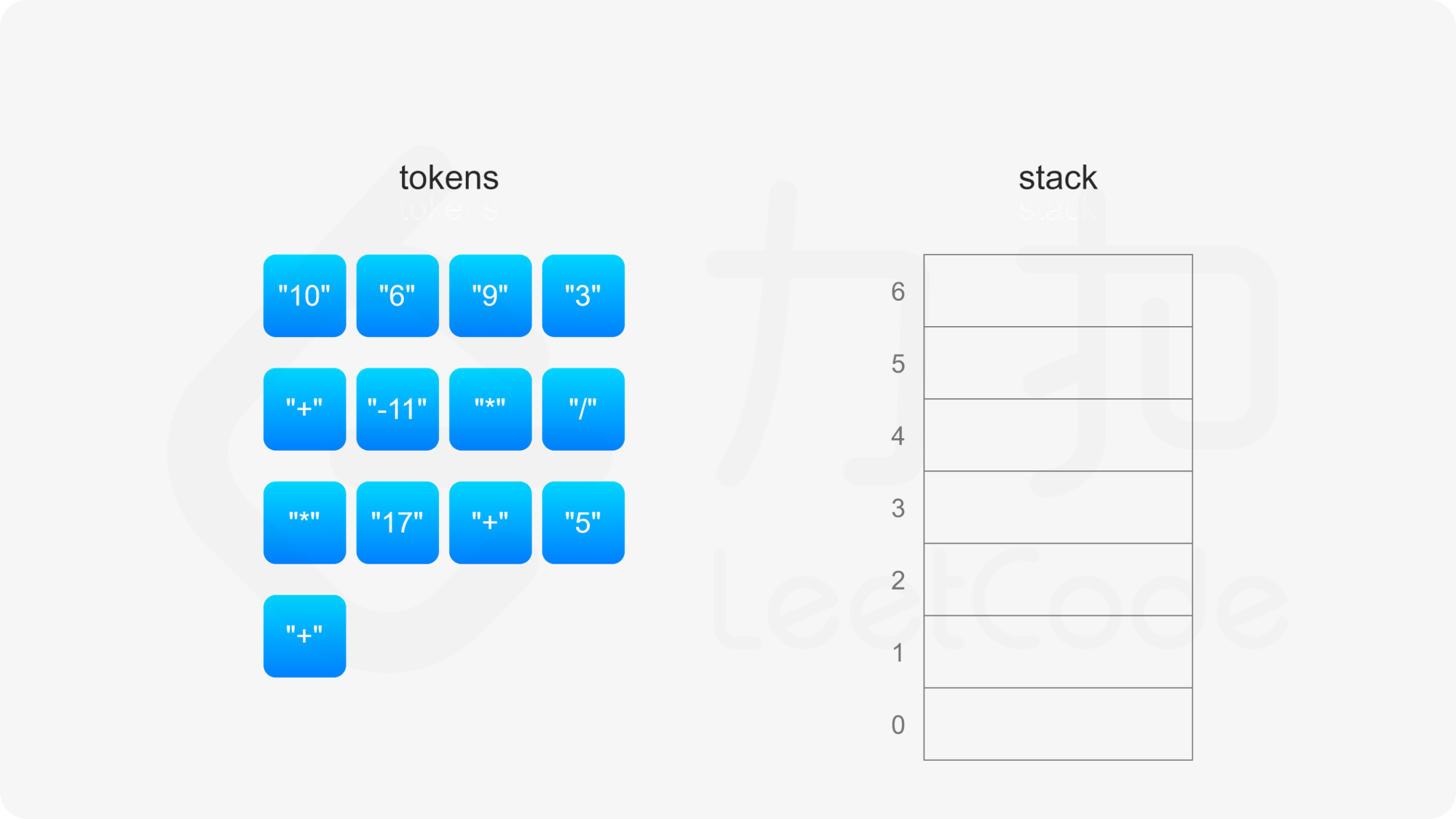
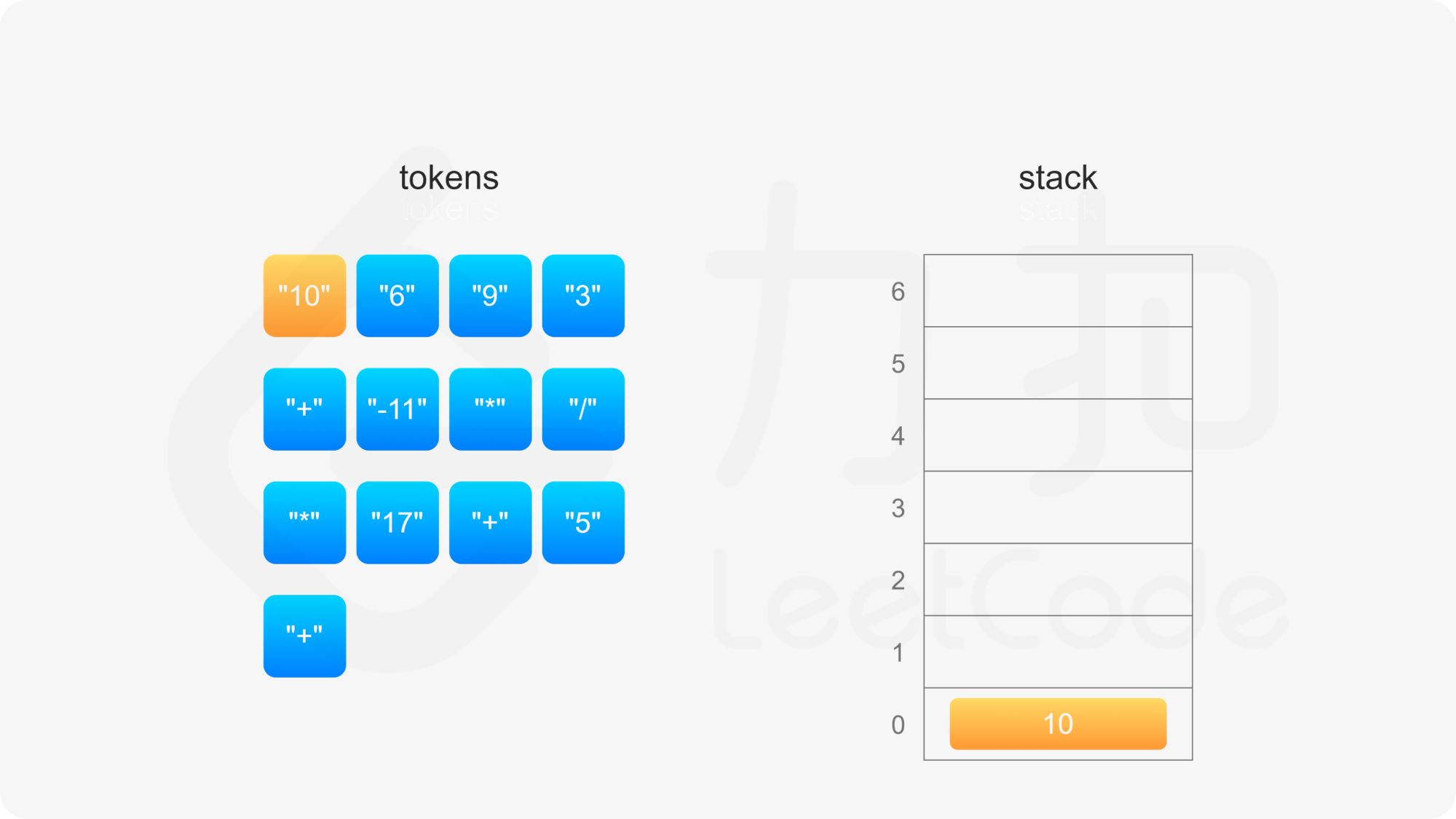
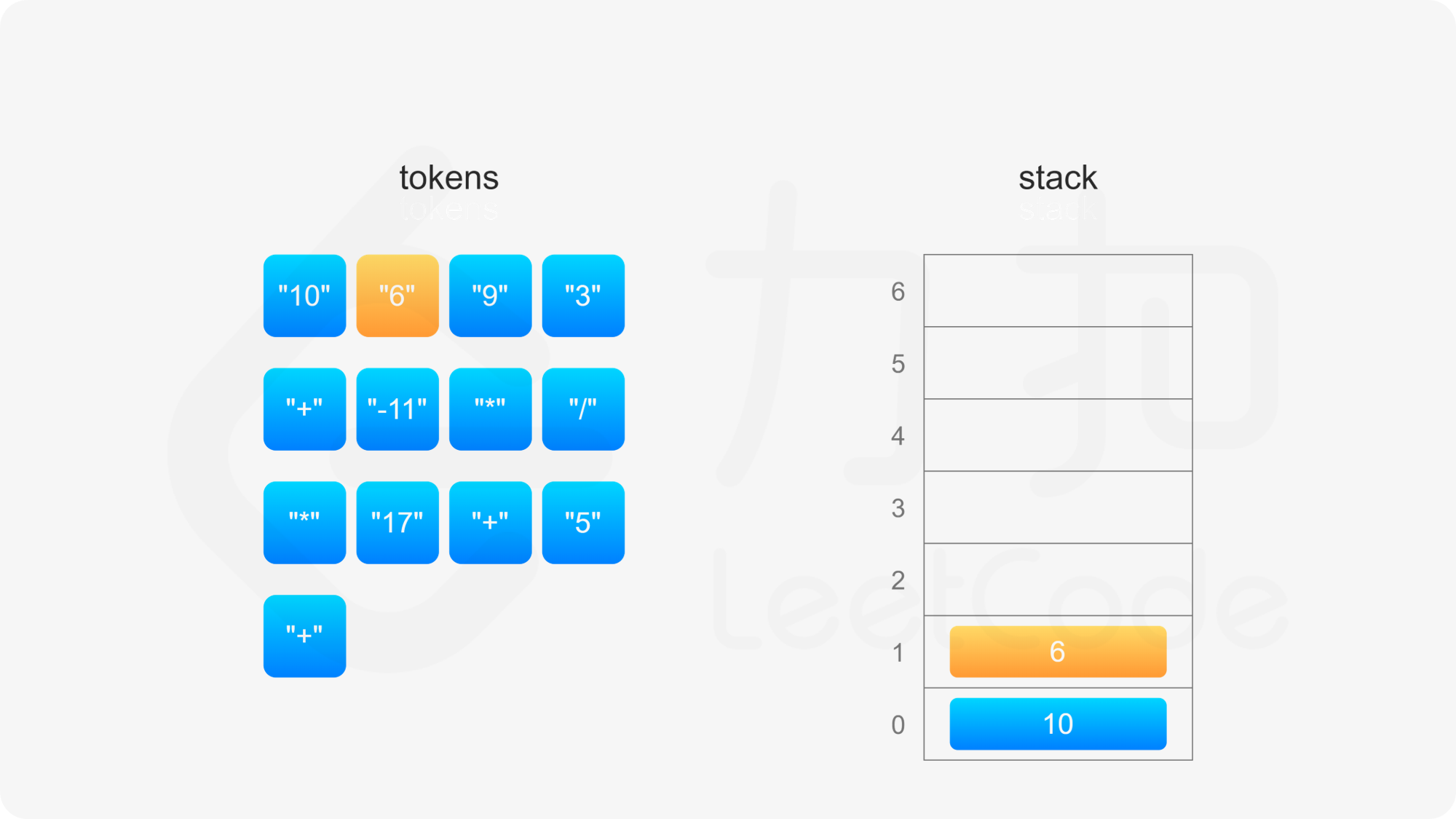
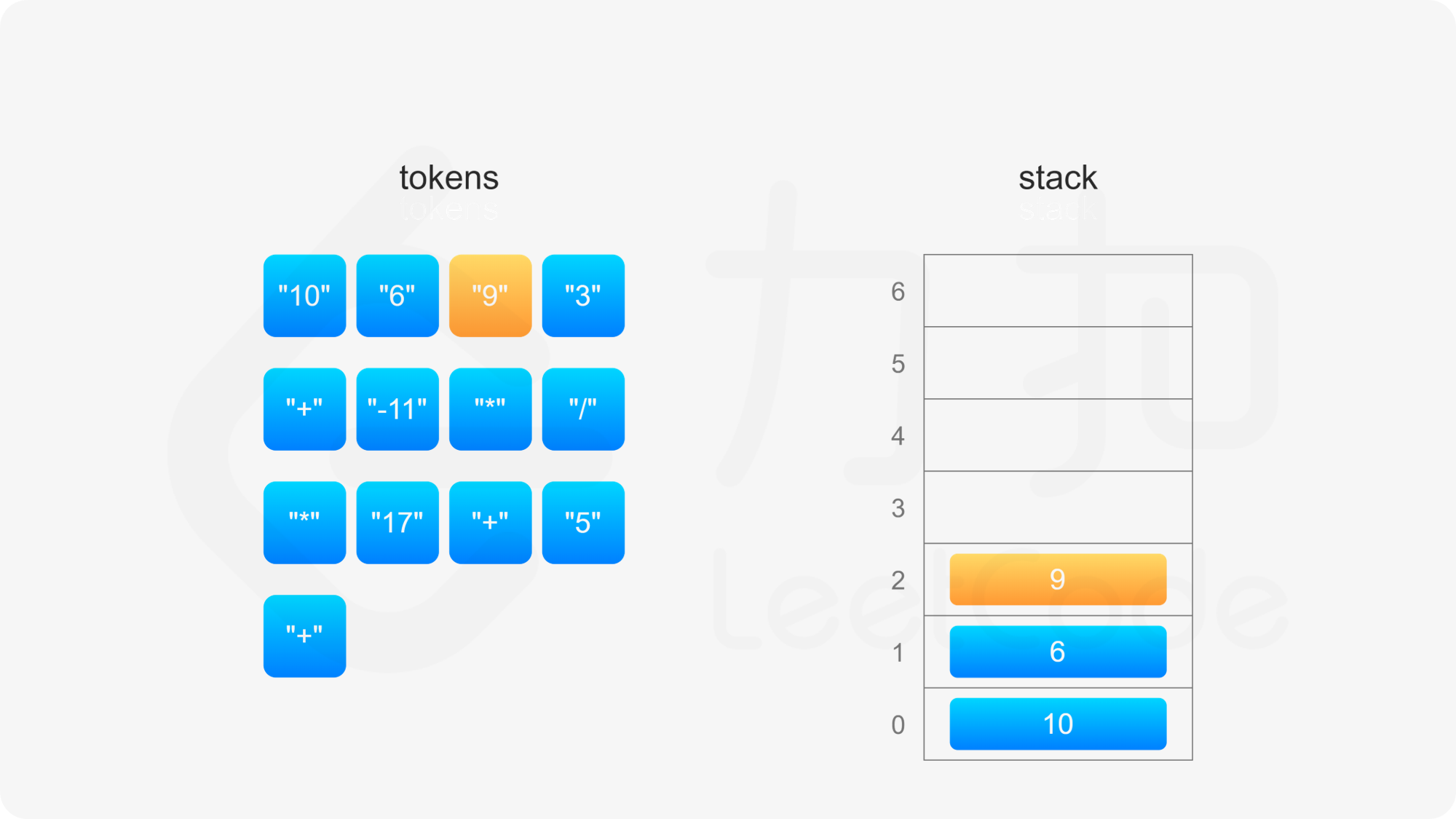
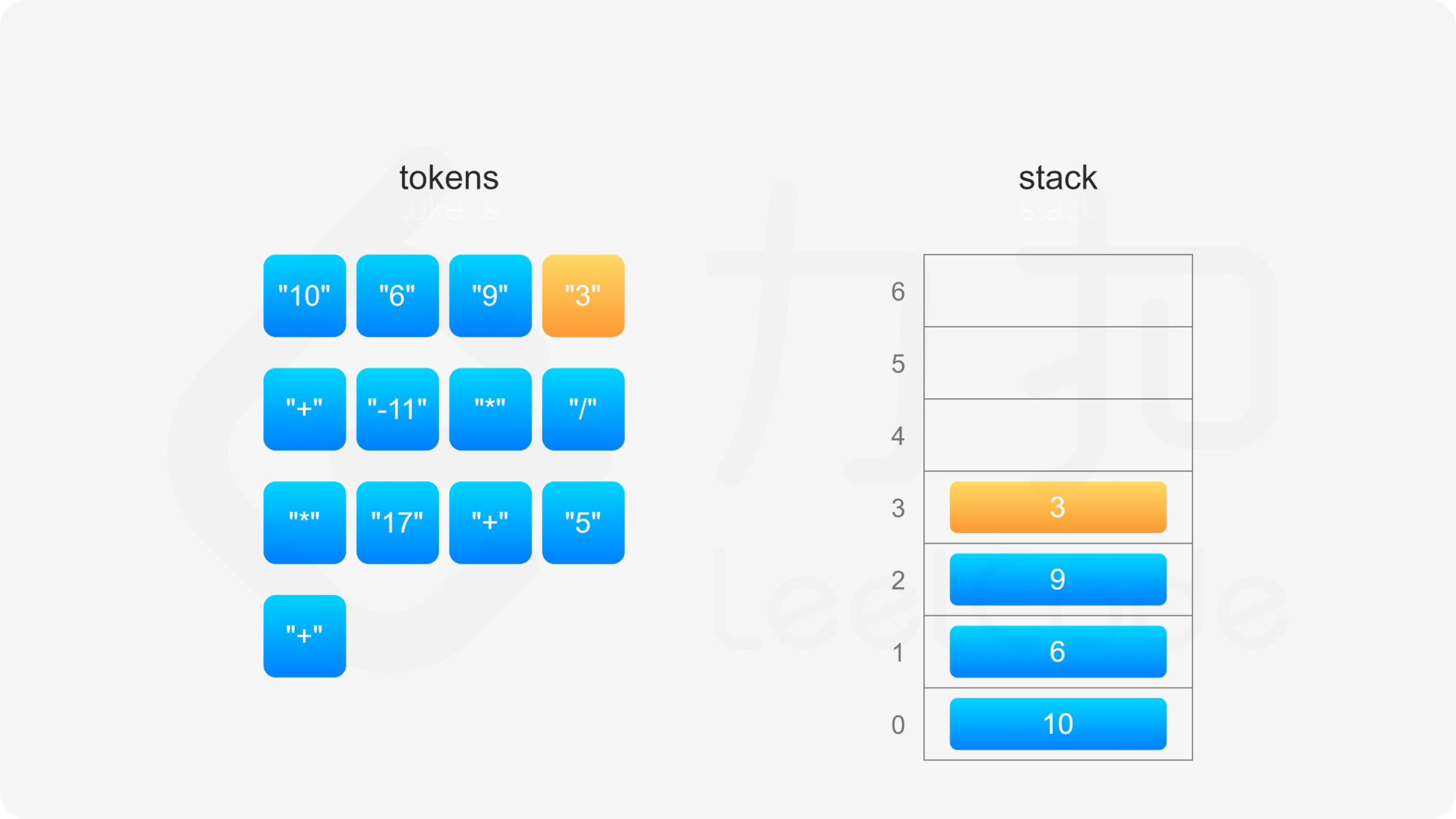
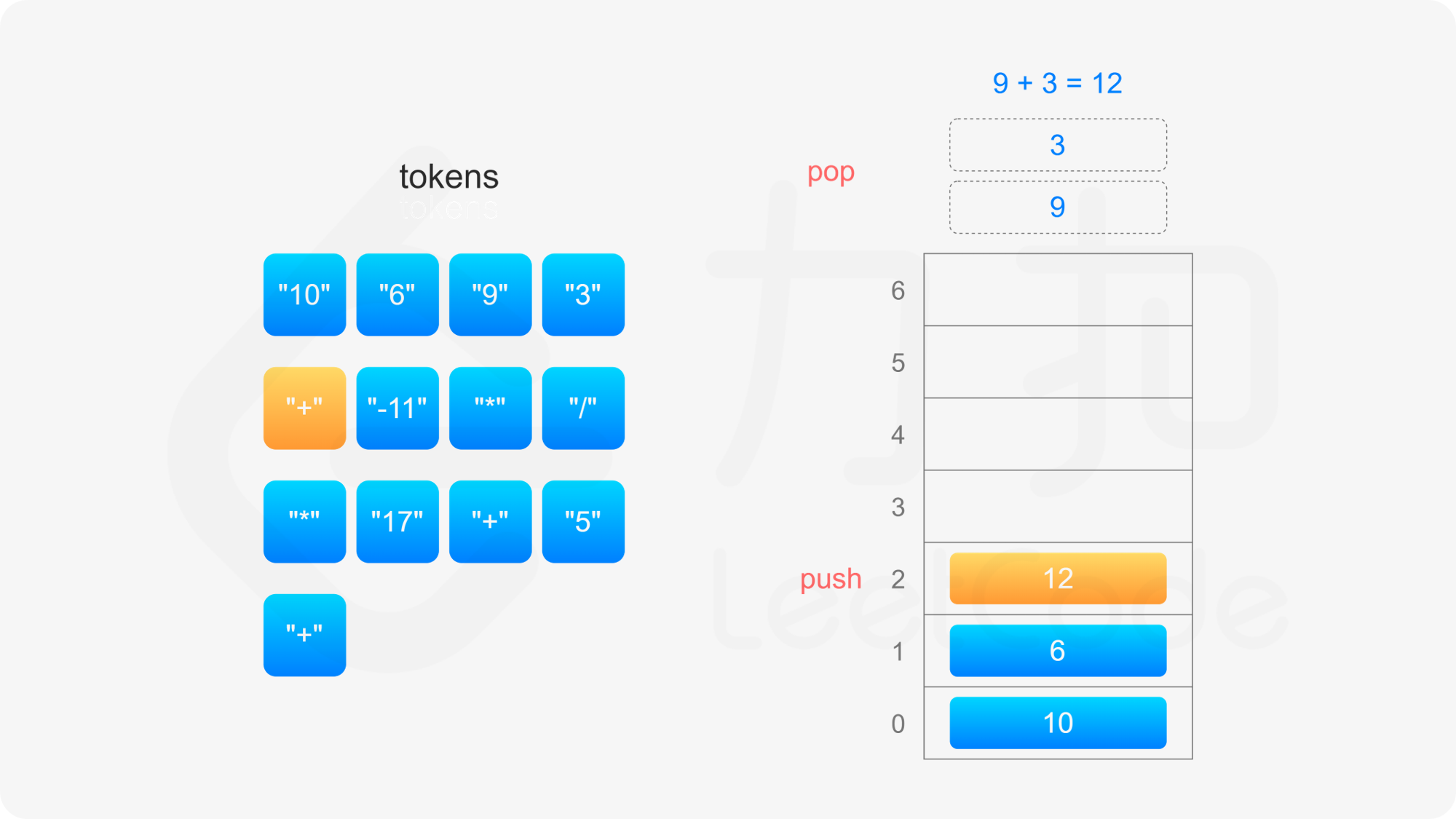
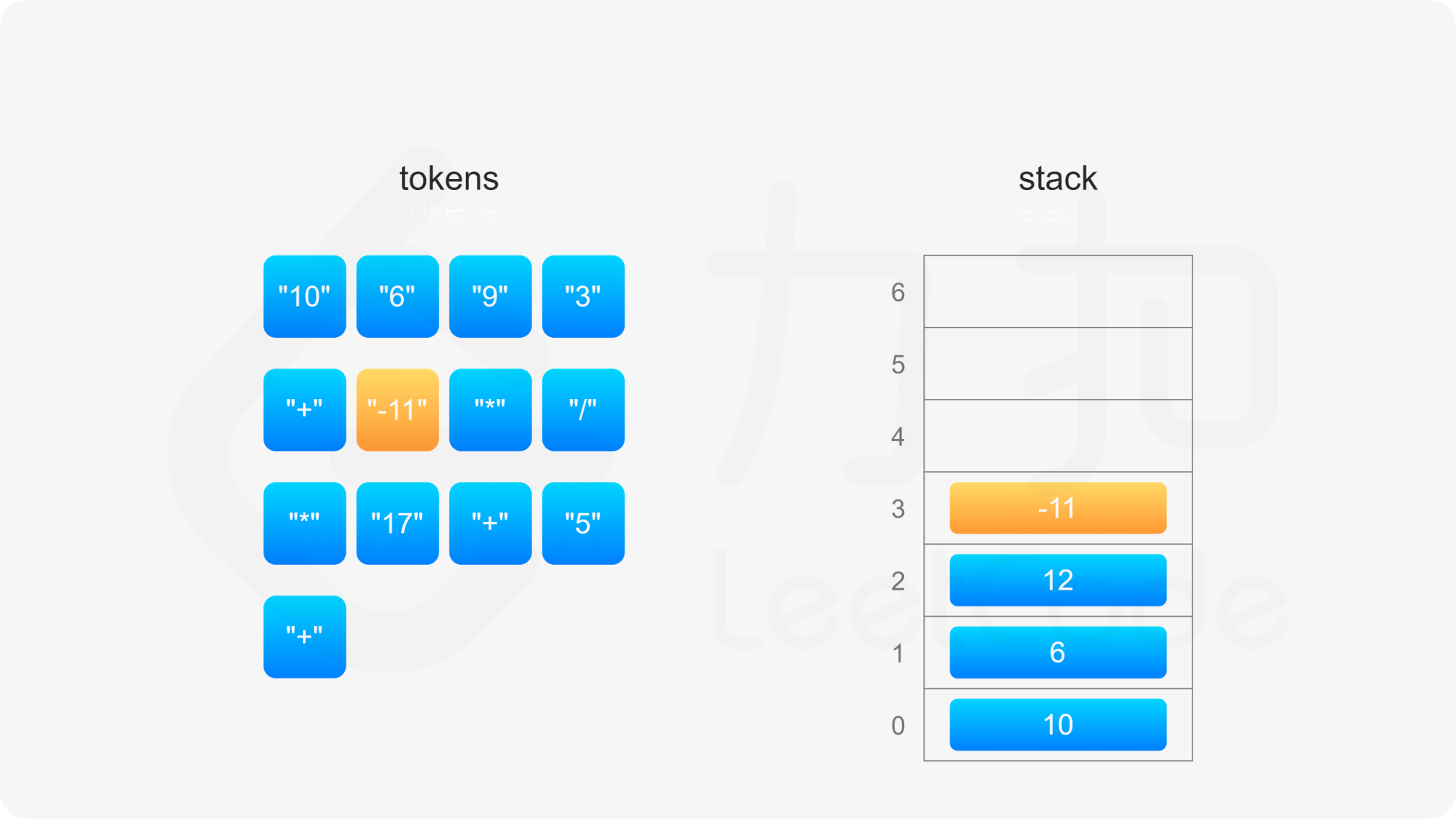
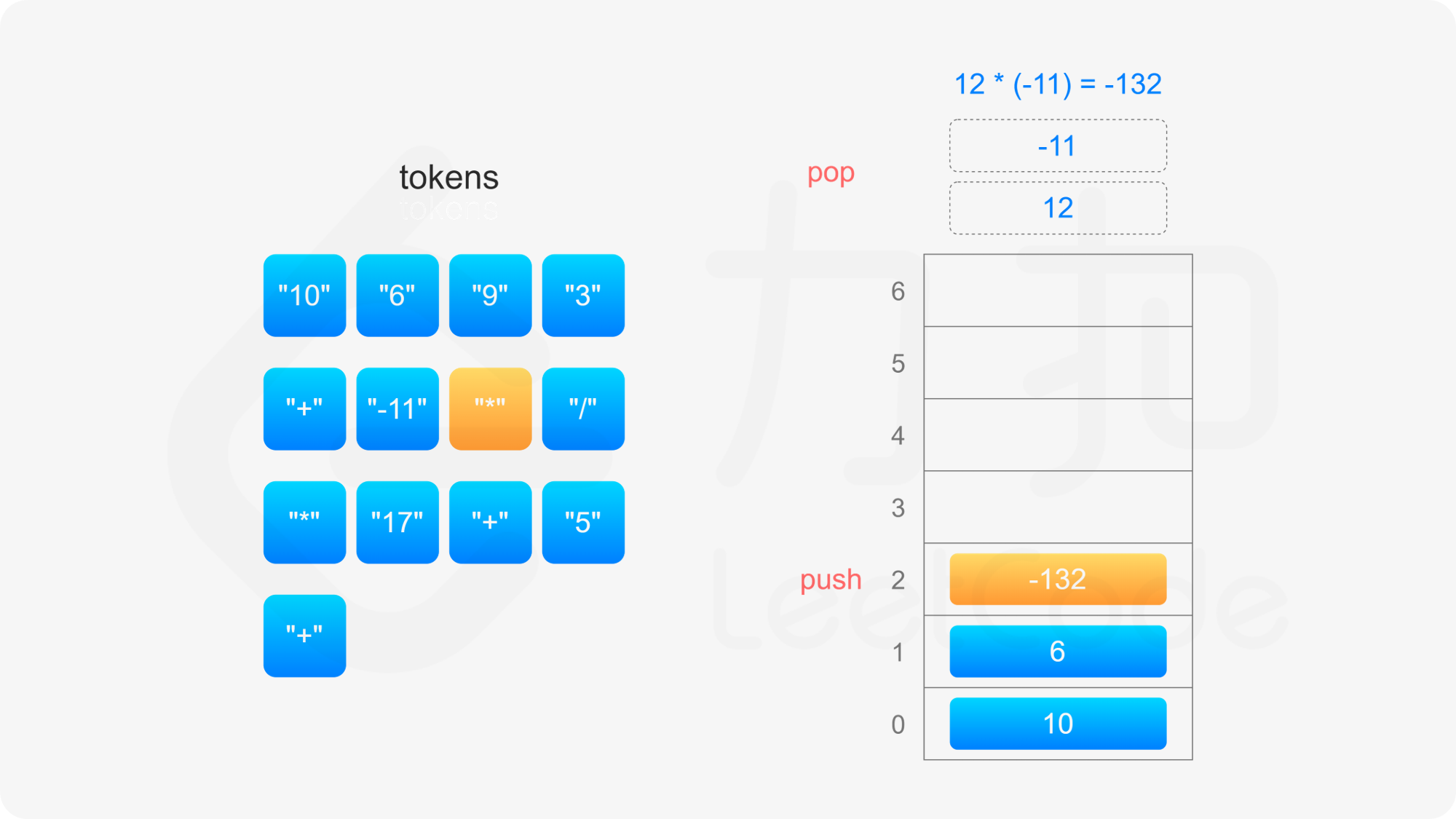
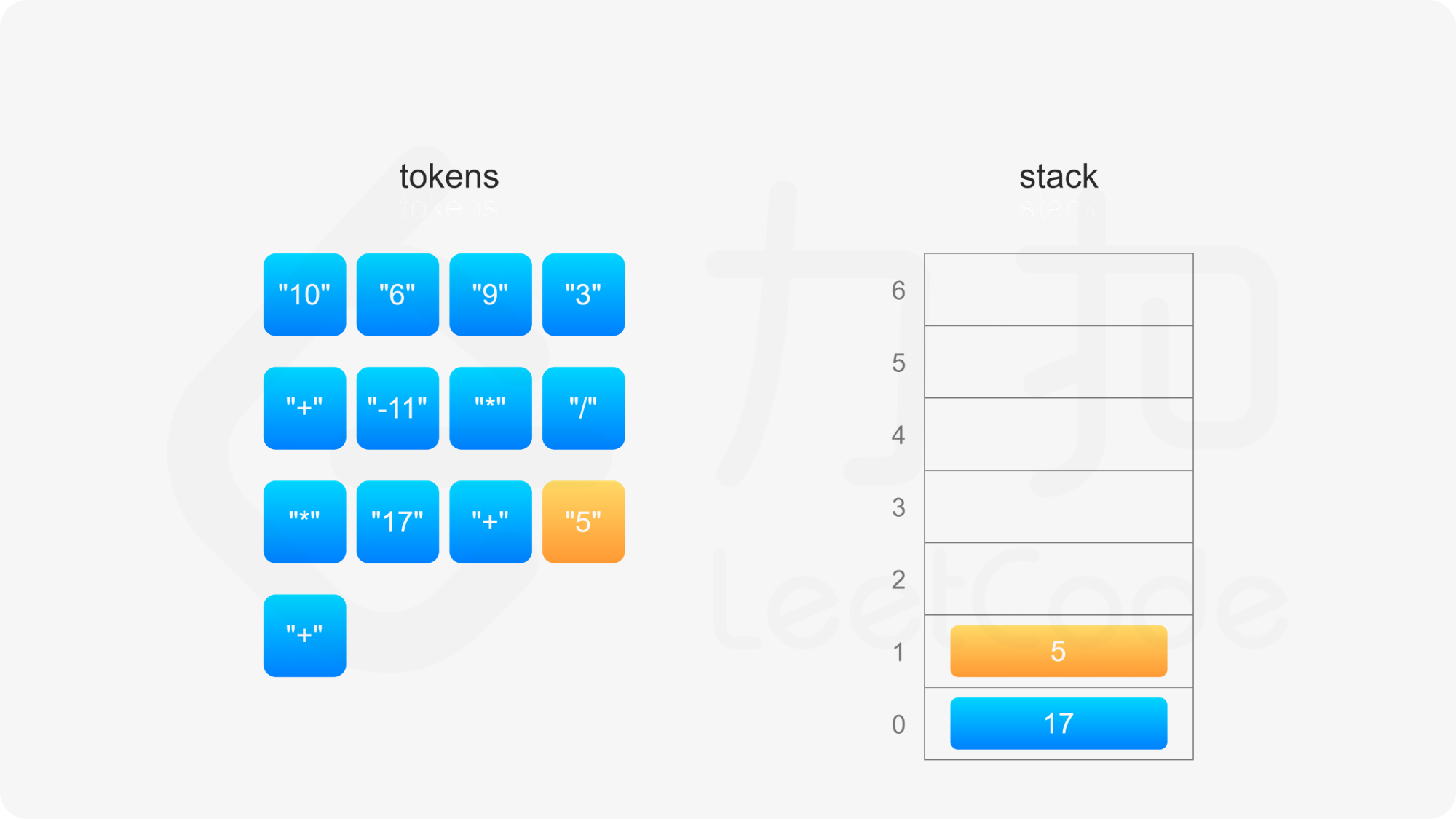
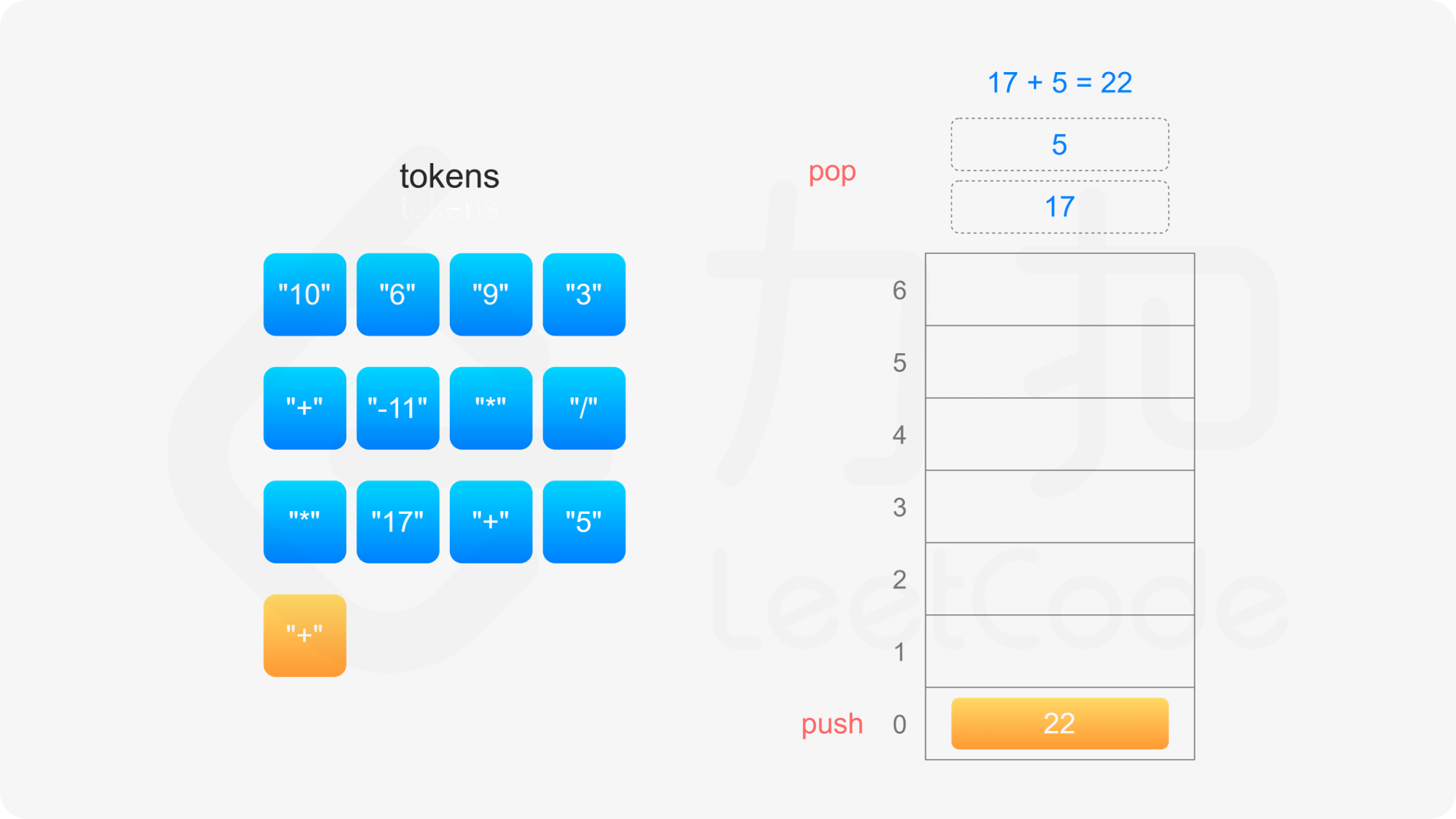
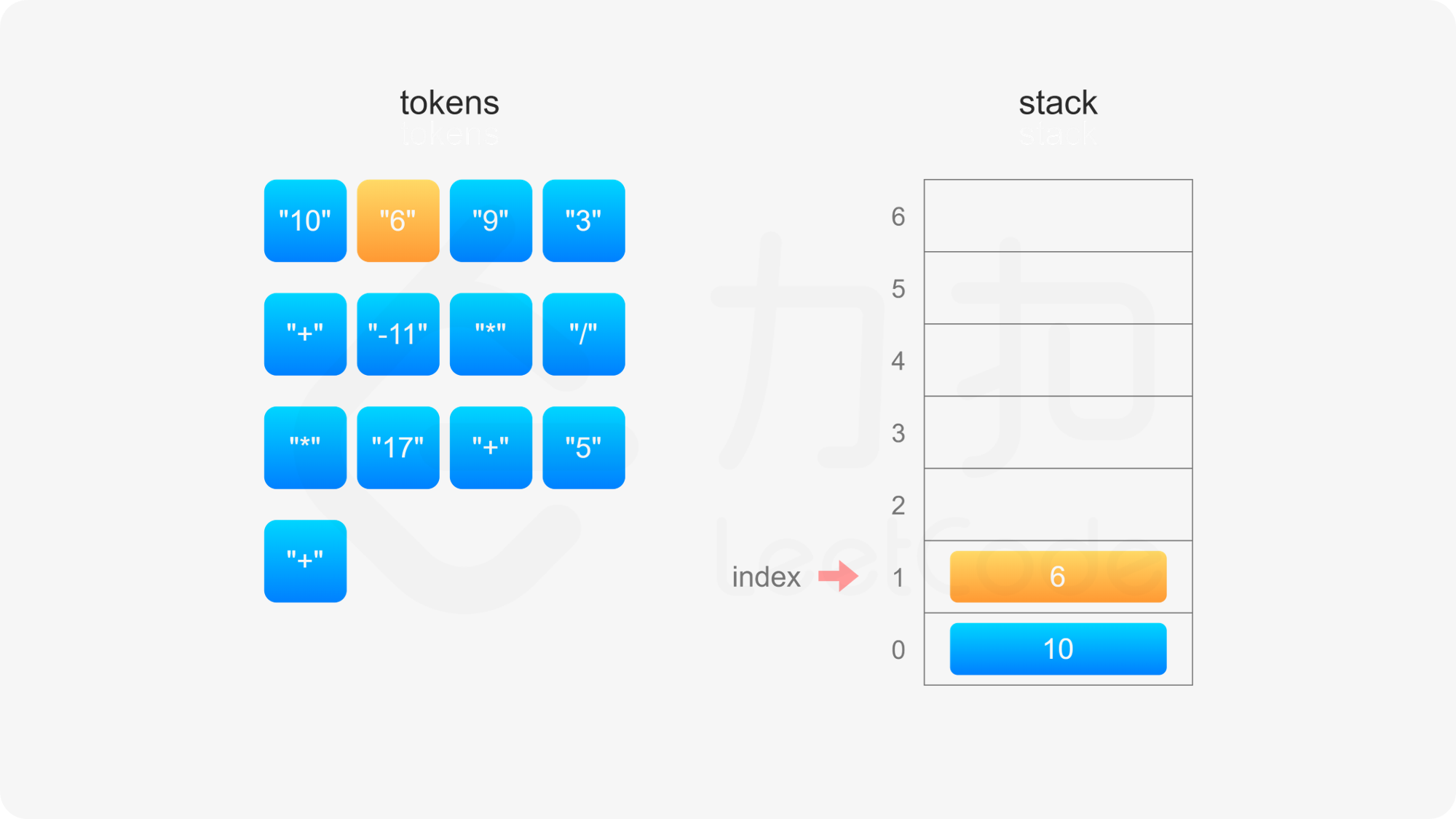
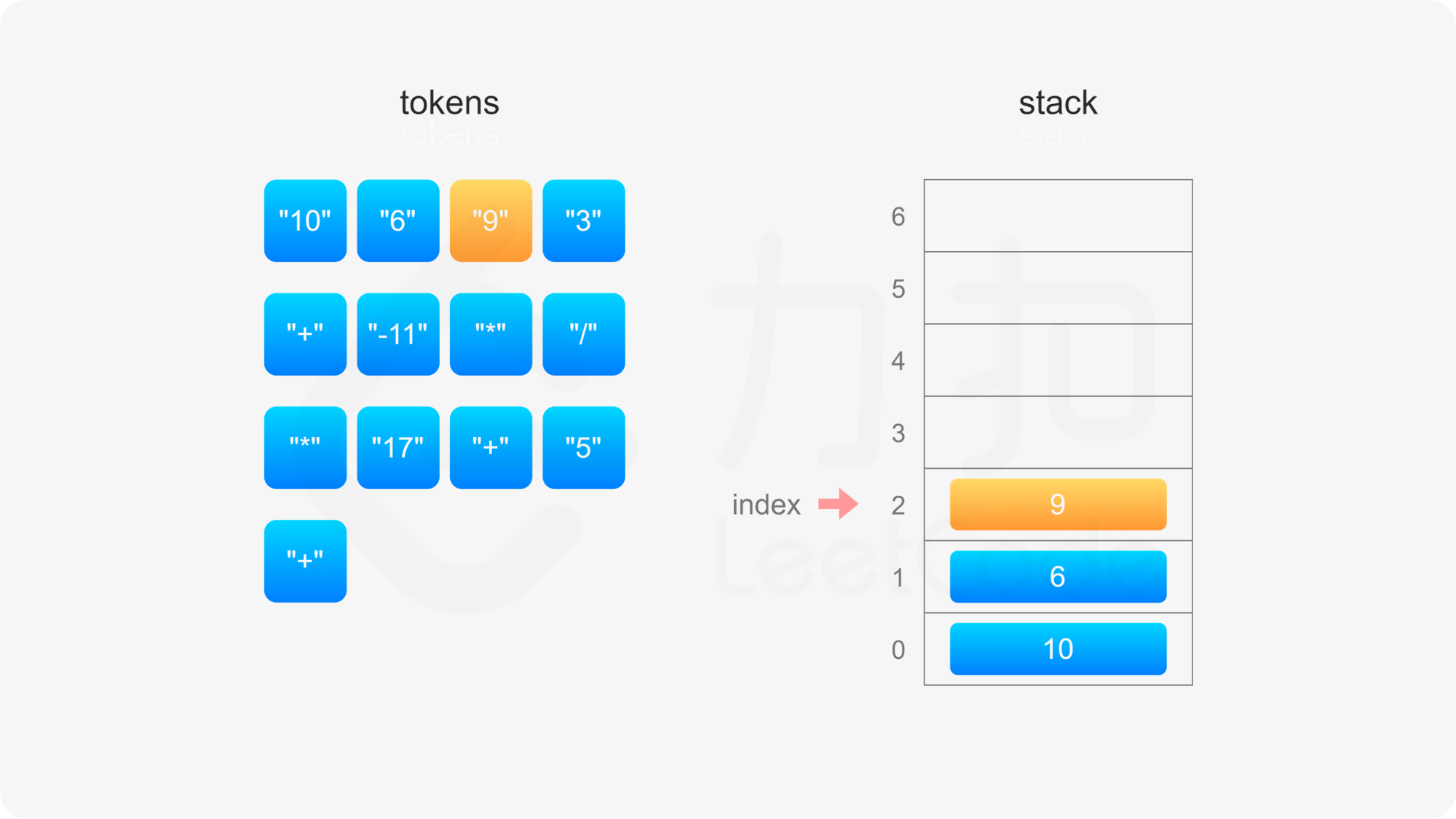
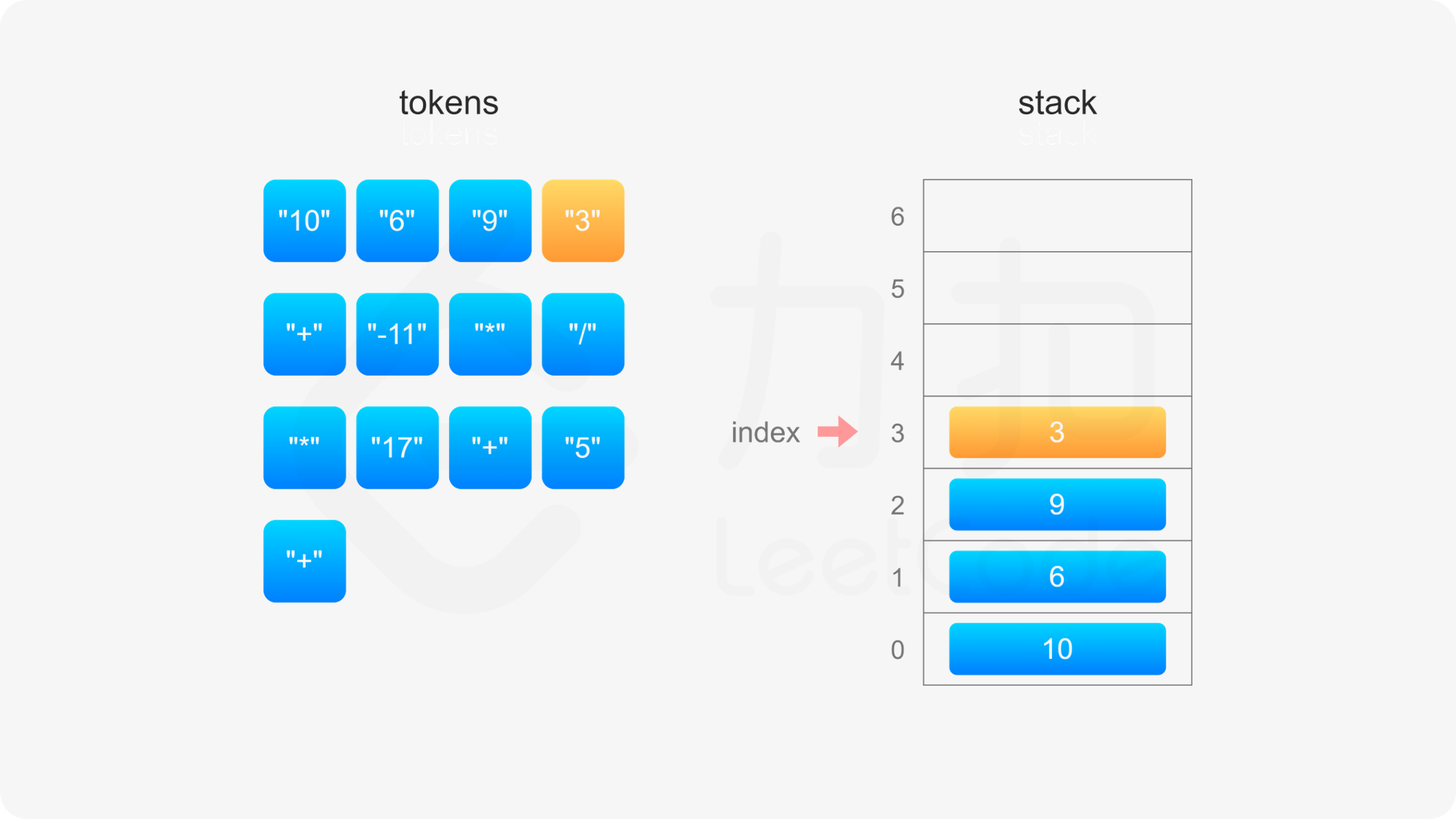
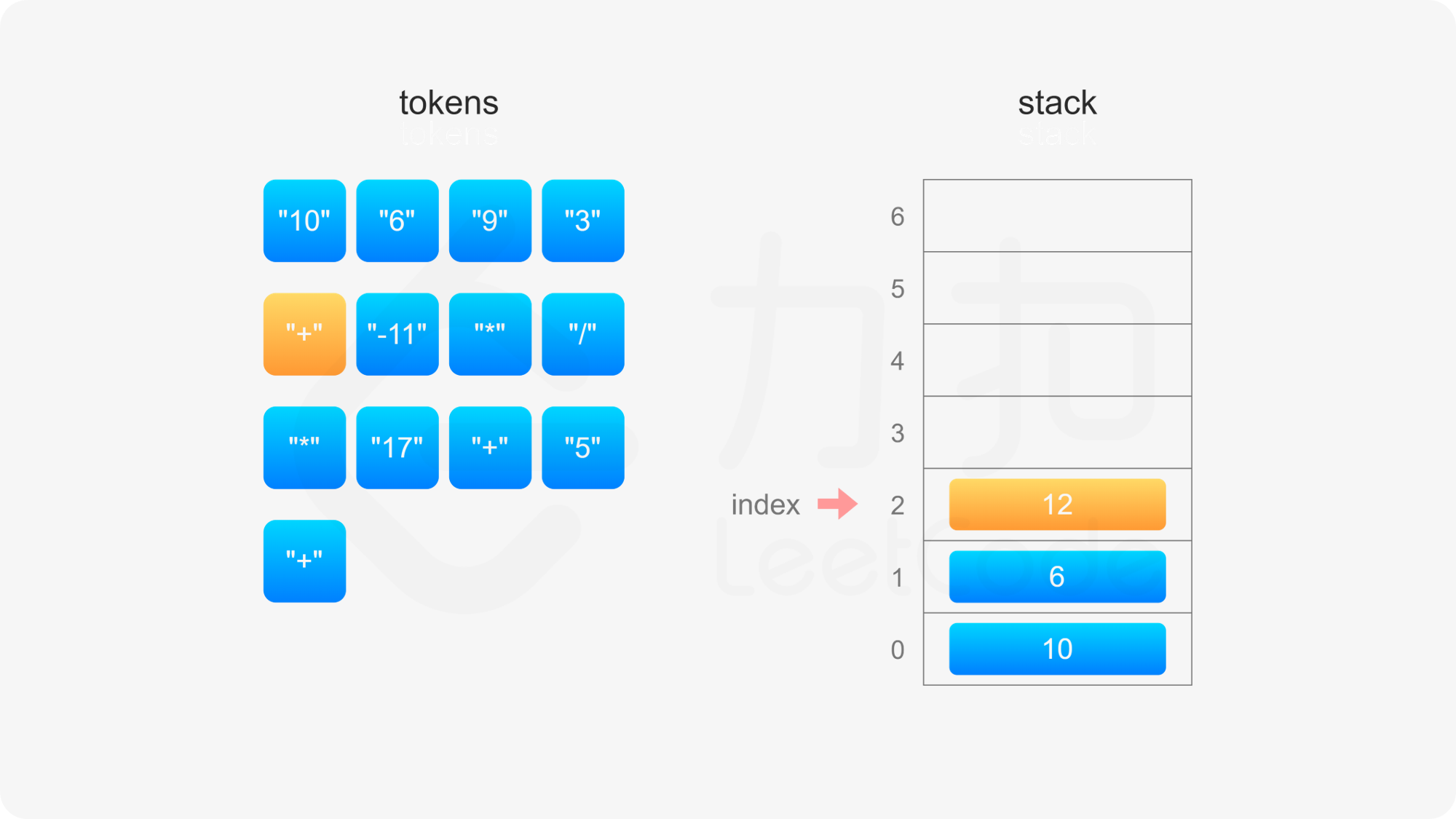
后缀表达式严格遵循「从左到右」的运算。计算后缀表达式的值时，使用一个栈存储操作数，从左到右遍历后缀表达式，进行如下操作：

  • 如果遇到操作数，则将操作数入栈；

  • 如果遇到运算符，则将两个操作数出栈，其中先出栈的是右操作数，后出栈的是左操作数，使用运算符对两个操作数进行运算，将运算得到的新操作数入栈。

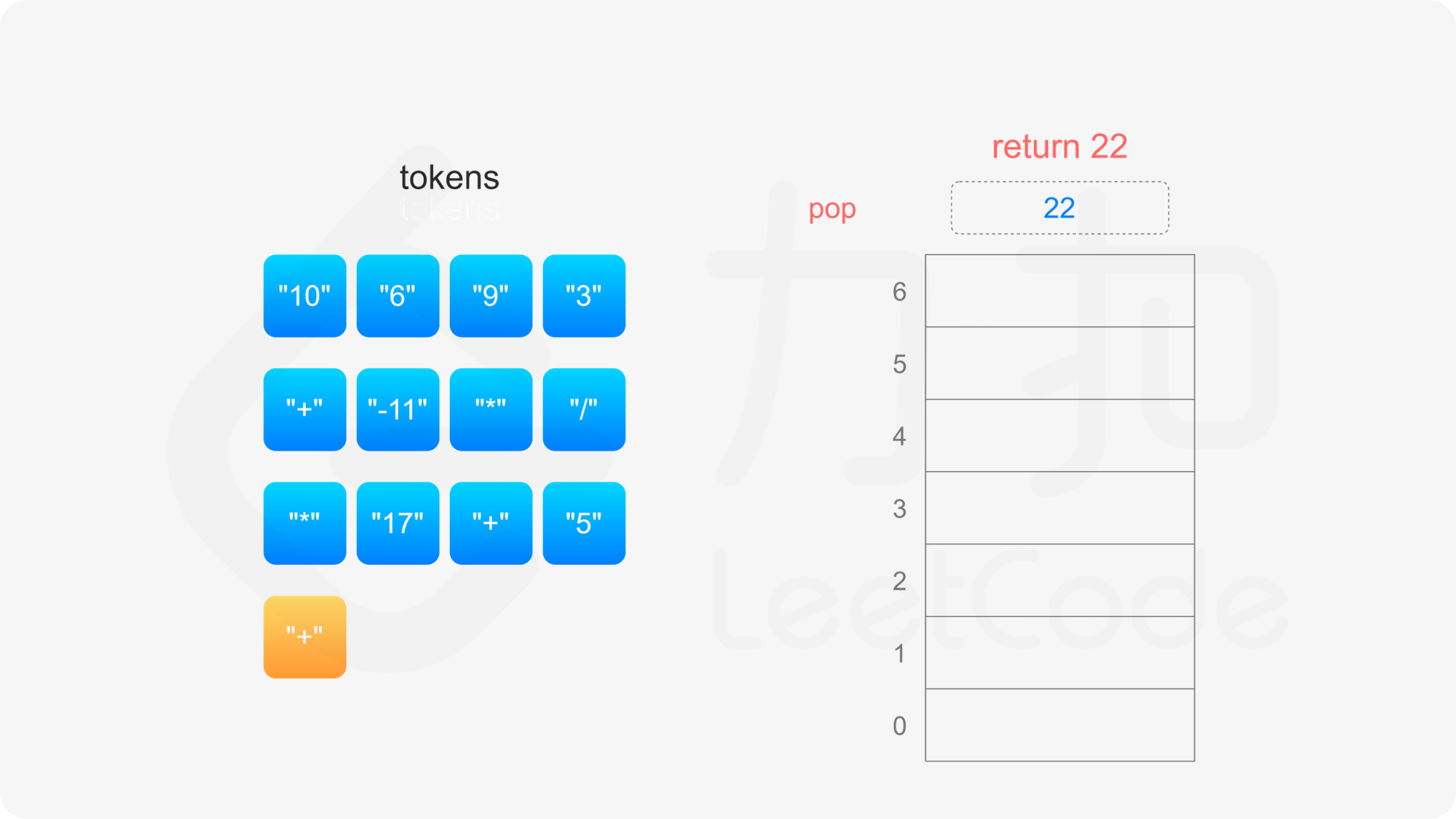
整个后缀表达式遍历完毕之后，栈内只有一个元素，该元素即为后缀表达式的值。

<ppt1,ppt2,ppt3,ppt4,ppt5,ppt6,ppt7,ppt8,ppt9,ppt10,ppt11,ppt12,ppt13,ppt14,ppt15>

[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> stack = new LinkedList<Integer>();
        int n = tokens.length;
        for (int i = 0; i < n; i++) {
            String token = tokens[i];
            if (isNumber(token)) {
                stack.push(Integer.parseInt(token));
            } else {
                int num2 = stack.pop();
                int num1 = stack.pop();
                switch (token) {
                    case "+":
                        stack.push(num1 + num2);
                        break;
                    case "-":
                        stack.push(num1 - num2);
                        break;
                    case "*":
                        stack.push(num1 * num2);
                        break;
                    case "/":
                        stack.push(num1 / num2);
                        break;
                    default:
                }
            }
        }
        return stack.pop();
    }

    public boolean isNumber(String token) {
        return !("+".equals(token) || "-".equals(token) || "*".equals(token) || "/".equals(token));
    }
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
var evalRPN = function(tokens) {
    const stack = [];
    const n = tokens.length;
    for (let i = 0; i < n; i++) {
        const token = tokens[i];
        if (isNumber(token)) {
            stack.push(parseInt(token));
        } else {
            const num2 = stack.pop();
            const num1 = stack.pop();
            if (token === '+') {
                stack.push(num1 + num2);
            } else if (token === '-') {
                stack.push(num1 - num2);
            } else if (token === '*') {
                stack.push(num1 * num2);
            } else if (token === '/') {
                stack.push(num1 / num2 > 0 ? Math.floor(num1 / num2) : Math.ceil(num1 / num2));
            }
        }
    }
    return stack.pop();
};

const isNumber = (token) => {
    return !('+' === token || '-' === token || '*' === token || '/' === token );
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func evalRPN(tokens []string) int {
    stack := []int{}
    for _, token := range tokens {
        val, err := strconv.Atoi(token)
        if err == nil {
            stack = append(stack, val)
        } else {
            num1, num2 := stack[len(stack)-2], stack[len(stack)-1]
            stack = stack[:len(stack)-2]
            switch token {
            case "+":
                stack = append(stack, num1+num2)
            case "-":
                stack = append(stack, num1-num2)
            case "*":
                stack = append(stack, num1*num2)
            default:
                stack = append(stack, num1/num2)
            }
        }
    }
    return stack[0]
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def evalRPN(self, tokens: List[str]) -> int:
        op_to_binary_fn = {
            "+": add,
            "-": sub,
            "*": mul,
            "/": lambda x, y: int(x / y),   # 需要注意 python 中负数除法的表现与题目不一致
        }

        stack = list()
        for token in tokens:
            try:
                num = int(token)
            except ValueError:
                num2 = stack.pop()
                num1 = stack.pop()
                num = op_to_binary_fn[token](num1, num2)
            finally:
                stack.append(num)
            
        return stack[0]
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<int> stk;
        int n = tokens.size();
        for (int i = 0; i < n; i++) {
            string& token = tokens[i];
            if (isNumber(token)) {
                stk.push(atoi(token.c_str()));
            } else {
                int num2 = stk.top();
                stk.pop();
                int num1 = stk.top();
                stk.pop();
                switch (token[0]) {
                    case '+':
                        stk.push(num1 + num2);
                        break;
                    case '-':
                        stk.push(num1 - num2);
                        break;
                    case '*':
                        stk.push(num1 * num2);
                        break;
                    case '/':
                        stk.push(num1 / num2);
                        break;
                }
            }
        }
        return stk.top();
    }

    bool isNumber(string& token) {
        return !(token == "+" || token == "-" || token == "*" || token == "/");
    }
};
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
bool isNumber(char* token) {
    return strlen(token) > 1 || ('0' <= token[0] && token[0] <= '9');
}

int evalRPN(char** tokens, int tokensSize) {
    int n = tokensSize;
    int stk[n], top = 0;
    for (int i = 0; i < n; i++) {
        char* token = tokens[i];
        if (isNumber(token)) {
            stk[top++] = atoi(token);
        } else {
            int num2 = stk[--top];
            int num1 = stk[--top];
            switch (token[0]) {
                case '+':
                    stk[top++] = num1 + num2;
                    break;
                case '-':
                    stk[top++] = num1 - num2;
                    break;
                case '*':
                    stk[top++] = num1 * num2;
                    break;
                case '/':
                    stk[top++] = num1 / num2;
                    break;
            }
        }
    }
    return stk[top - 1];
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 是数组 tokens 的长度。需要遍历数组 tokens 一次，计算后缀表达式的值。

  • 空间复杂度：O(n)，其中 n 是数组 tokens 的长度。使用栈存储计算过程中的数，栈内元素个数不会超过后缀表达式的长度。

方法二：数组模拟栈

方法一使用栈存储操作数。也可以使用一个数组模拟栈操作。

如果使用数组代替栈，则需要预先定义数组的长度。对于长度为 n 的后缀表达式，显然栈内元素个数不会超过 n，但是将数组的长度定义为 n 仍然超过了栈内元素个数的上界。那么，栈内元素最多可能有多少个？

对于一个有效的后缀表达式，其长度 n 一定是奇数，且操作数的个数一定比运算符的个数多 1 个，即包含 n+1/2 个操作数和 n-1/2 个运算符。考虑遇到操作数和运算符时，栈内元素个数分别会如何变化：

  • 如果遇到操作数，则将操作数入栈，因此栈内元素增加 1 个；

  • 如果遇到运算符，则将两个操作数出栈，然后将一个新操作数入栈，因此栈内元素先减少 2 个再增加 1 个，结果是栈内元素减少 1 个。

由此可以得到操作数和运算符与栈内元素个数变化的关系：遇到操作数时，栈内元素增加 1 个；遇到运算符时，栈内元素减少 1 个。

最坏情况下，n+1/2 个操作数都在表达式的前面，n-1/2 个运算符都在表达式的后面，此时栈内元素最多为 n+1/2 个。在其余情况下，栈内元素总是少于 n+1/2 个。因此，在任何情况下，栈内元素最多可能有 n+1/2 个，将数组的长度定义为 n+1/2 即可。

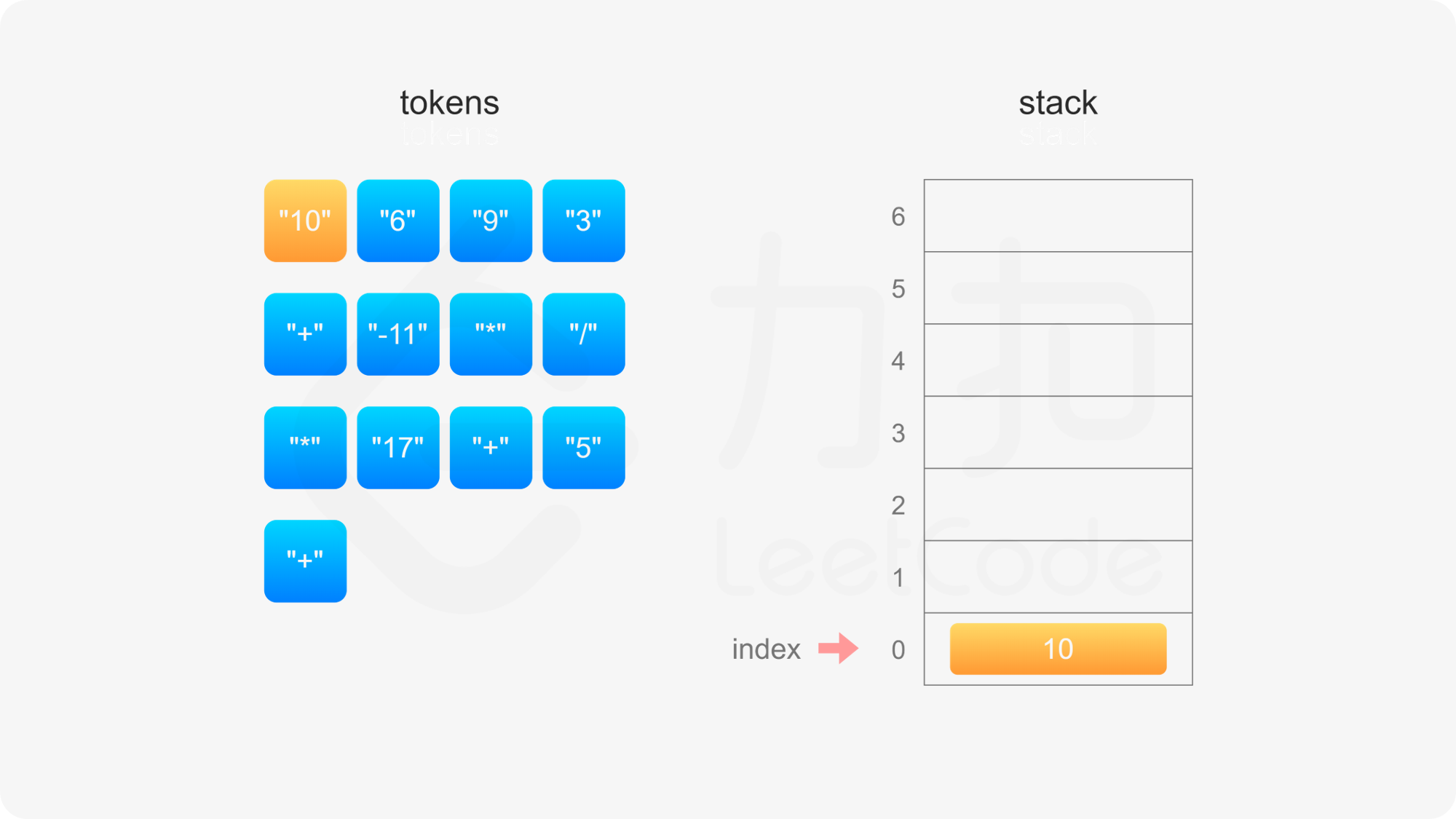
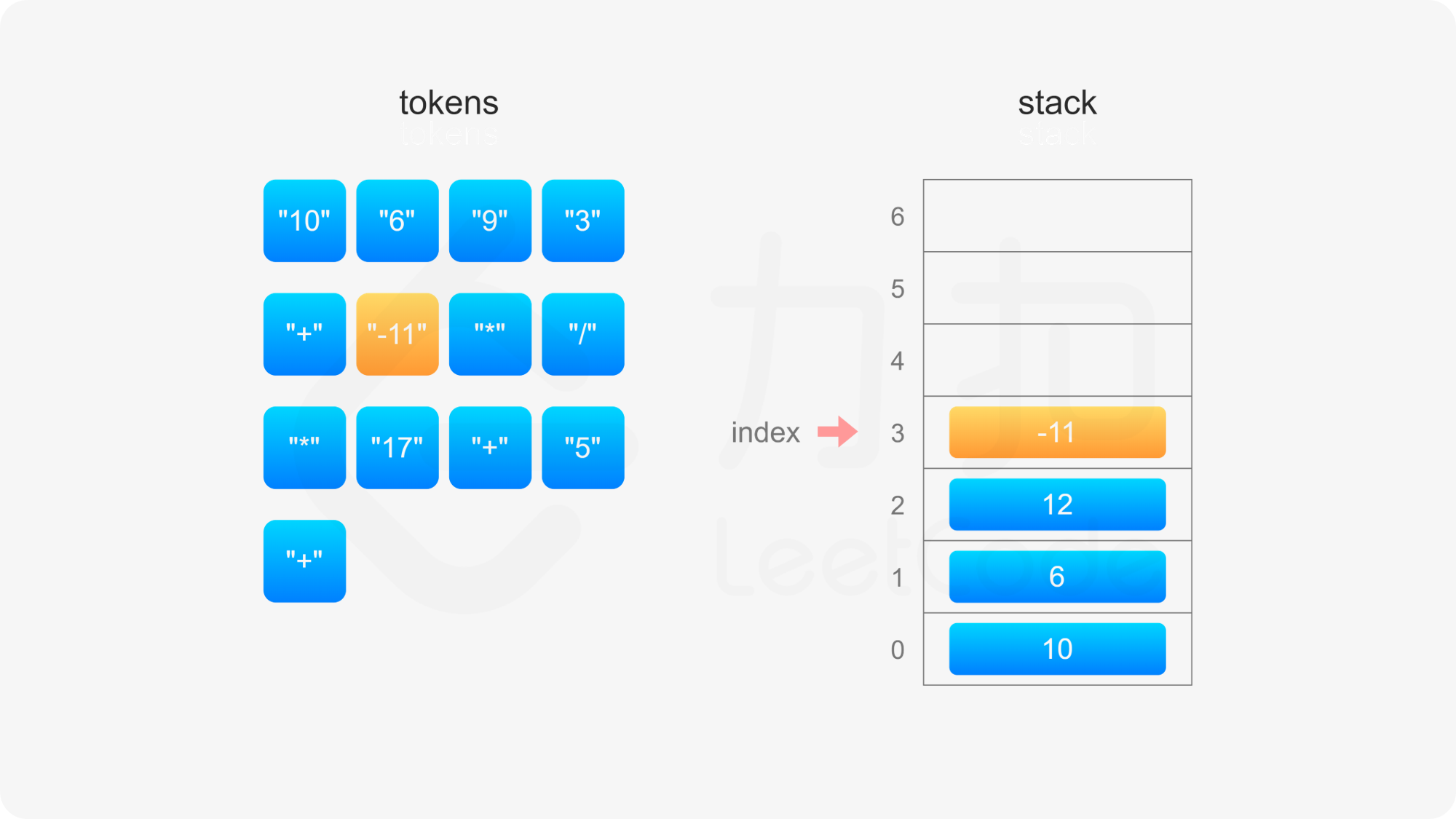
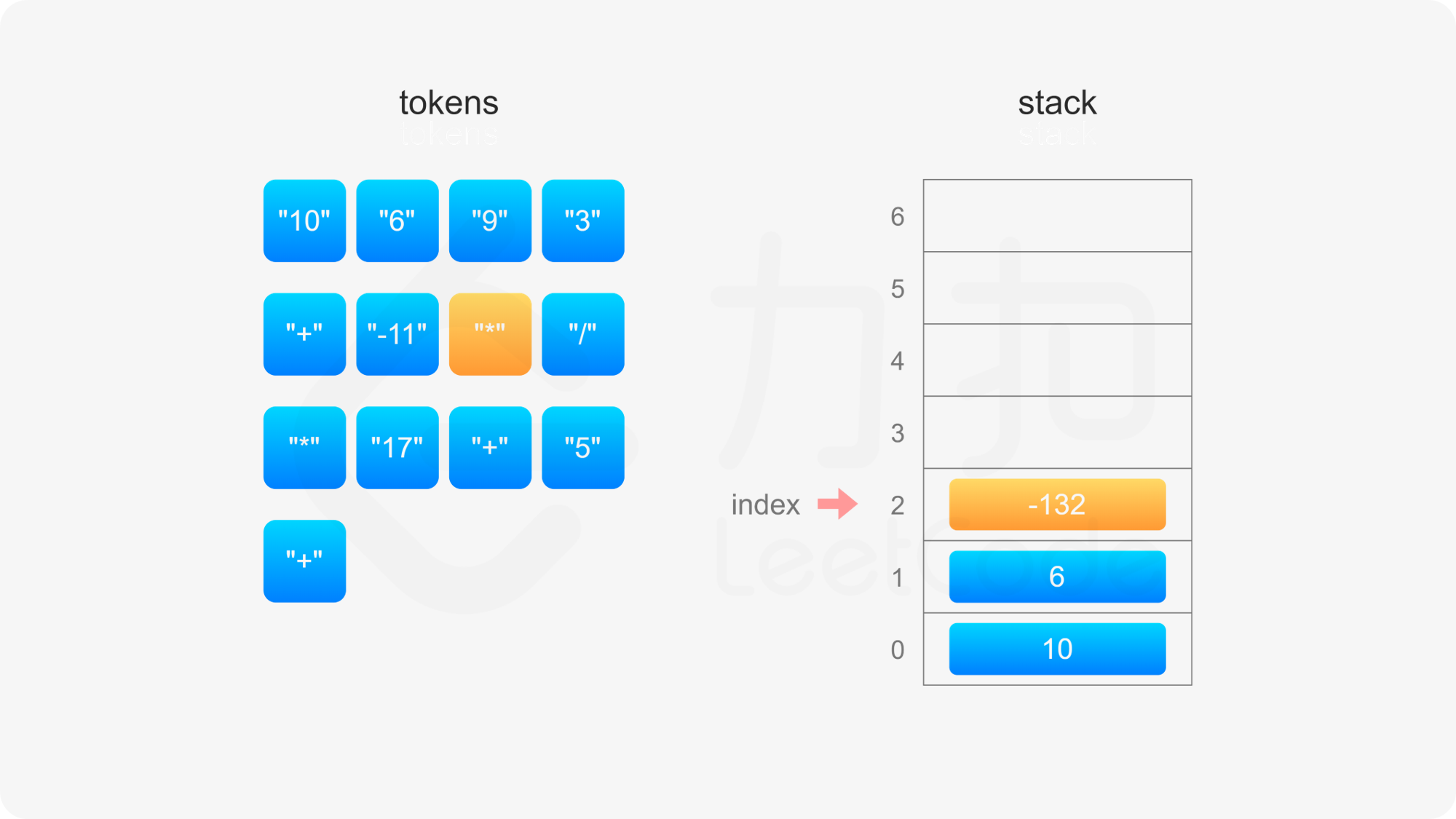
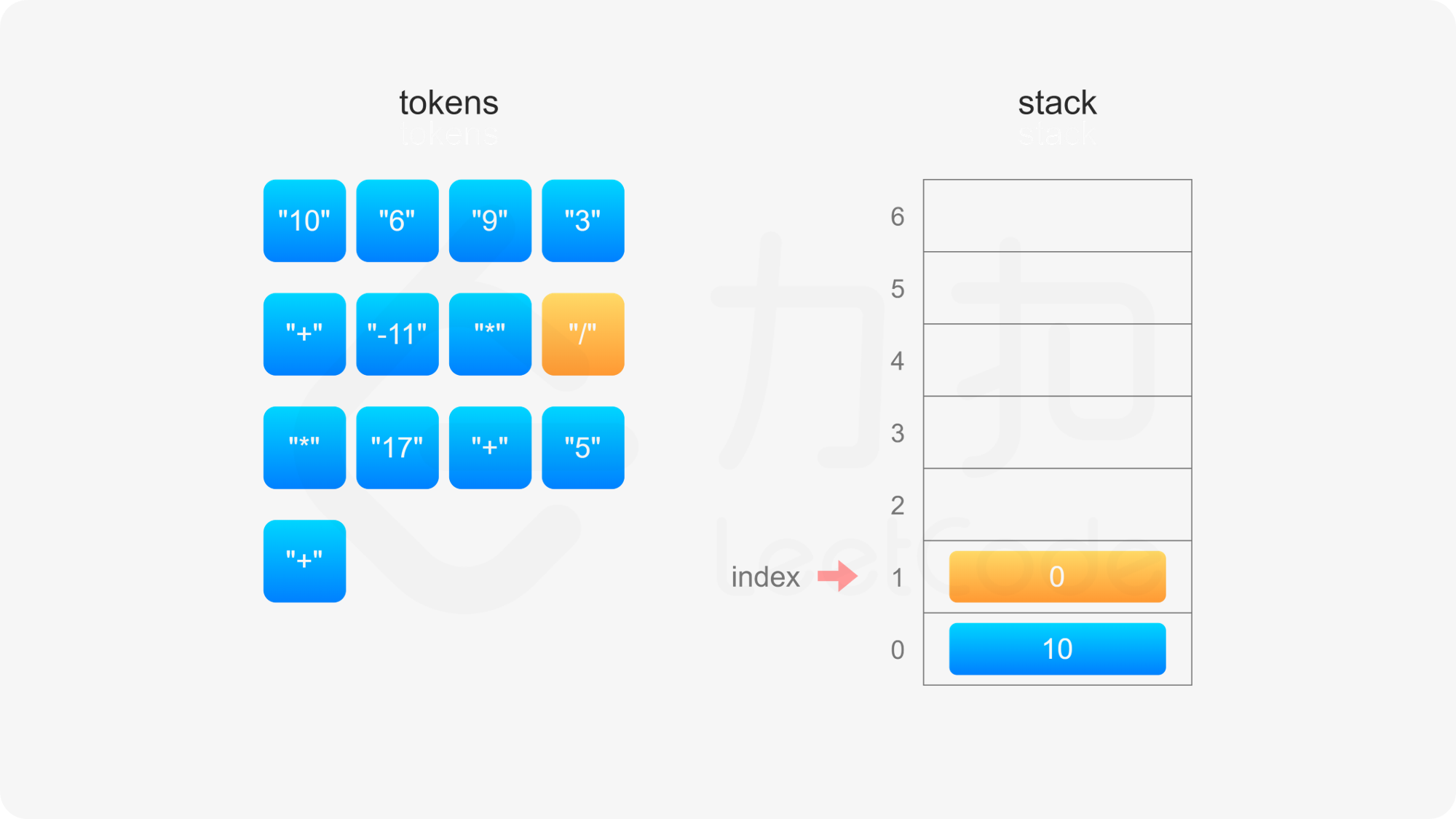
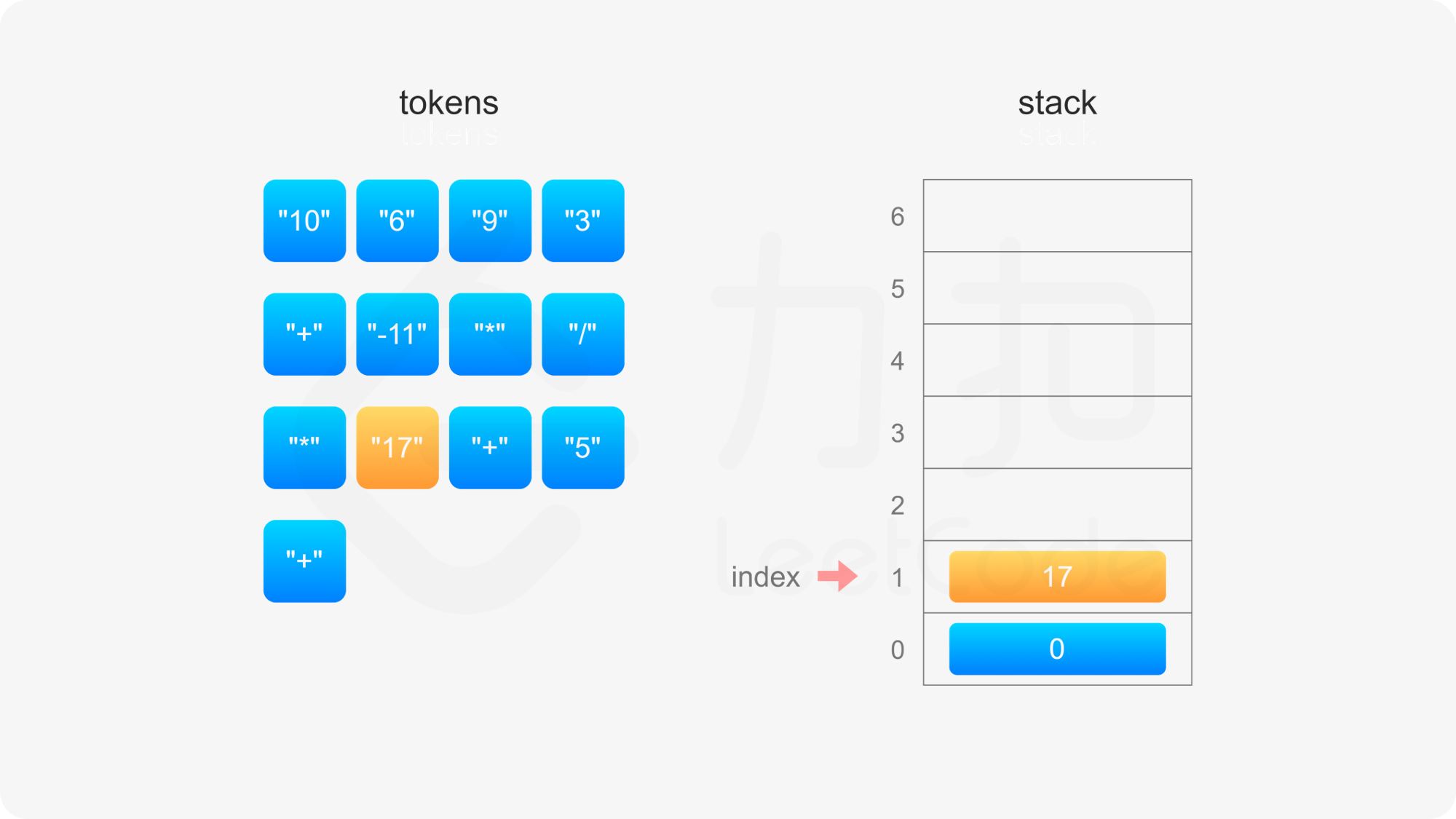
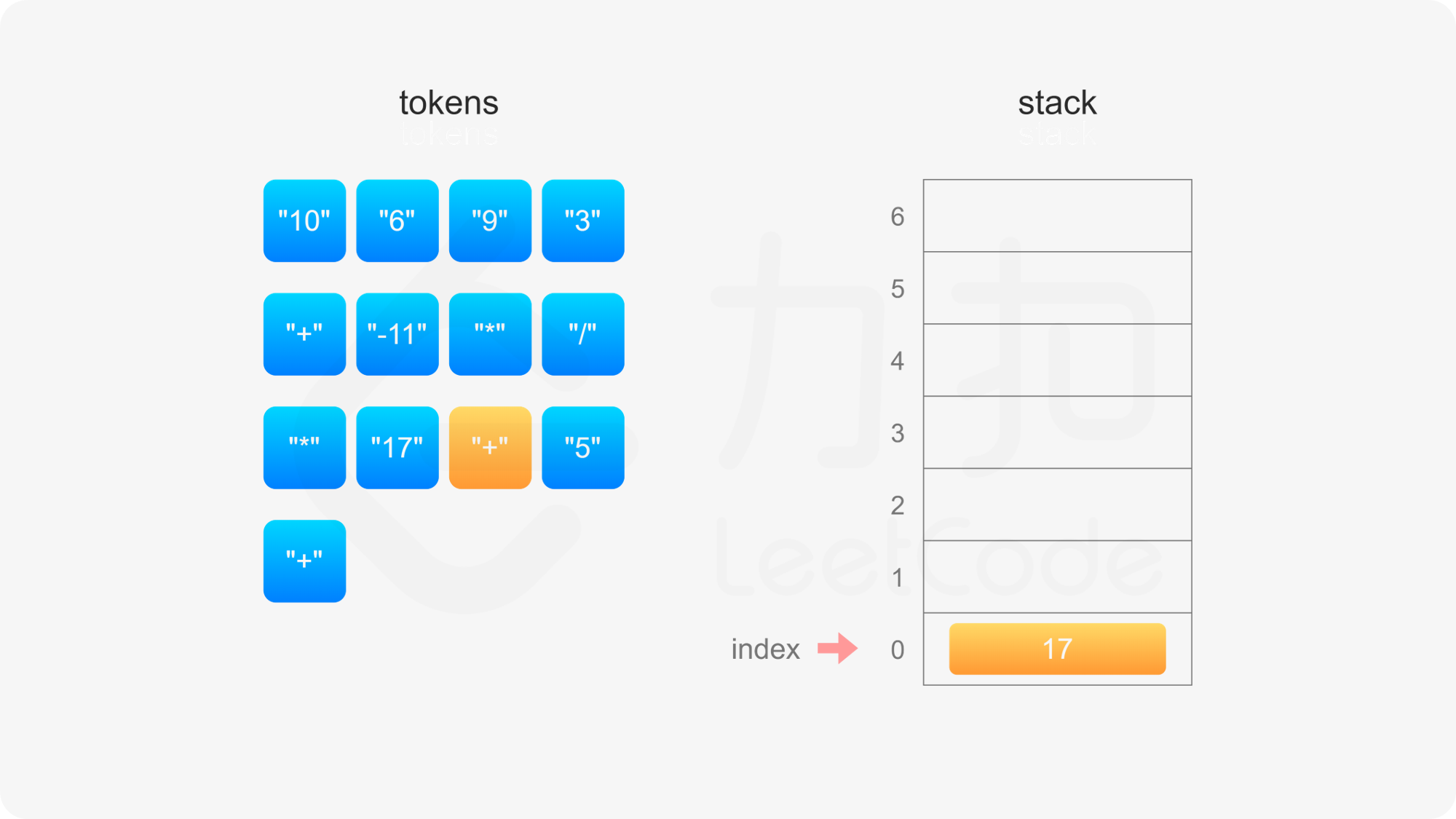
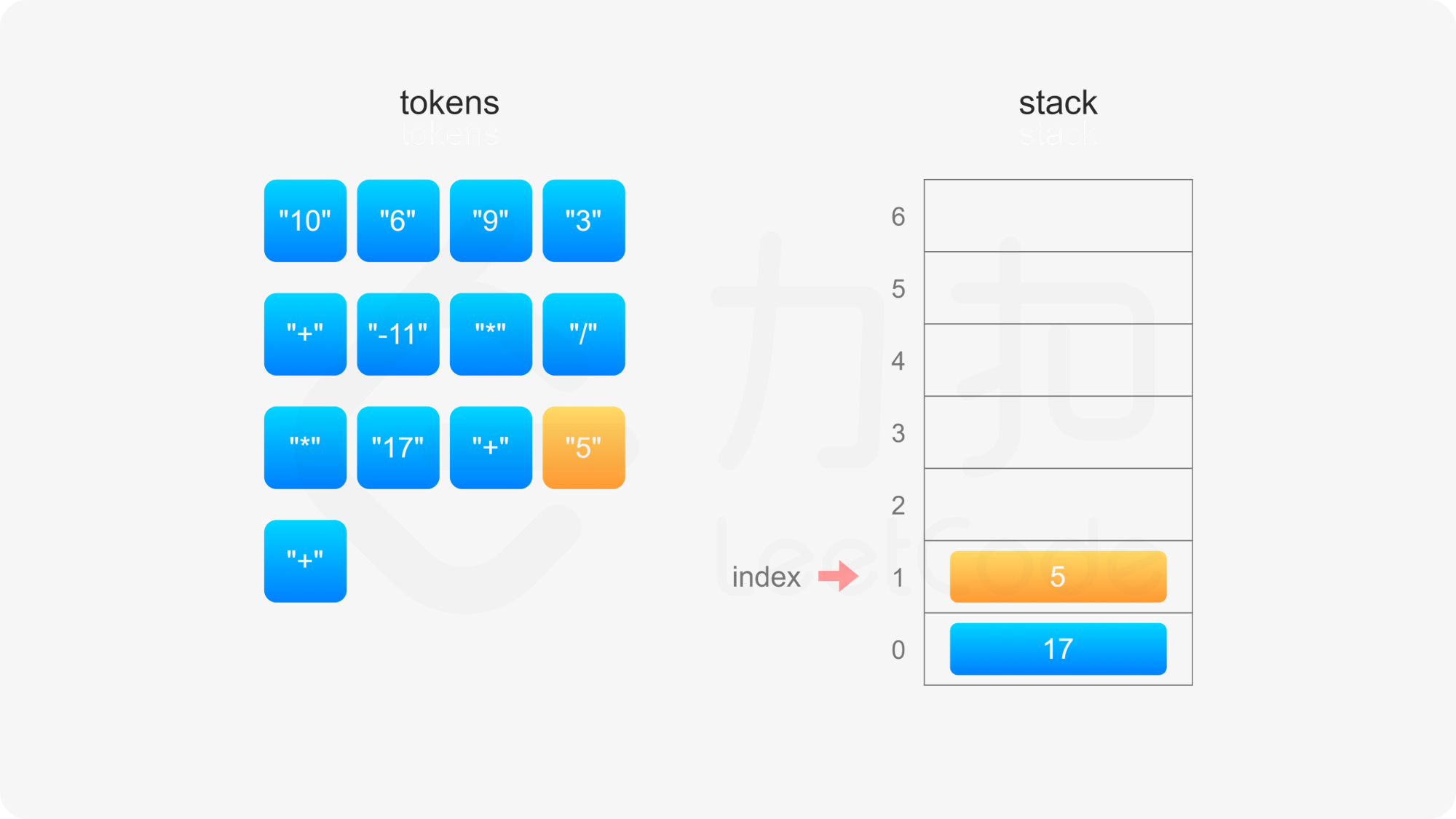
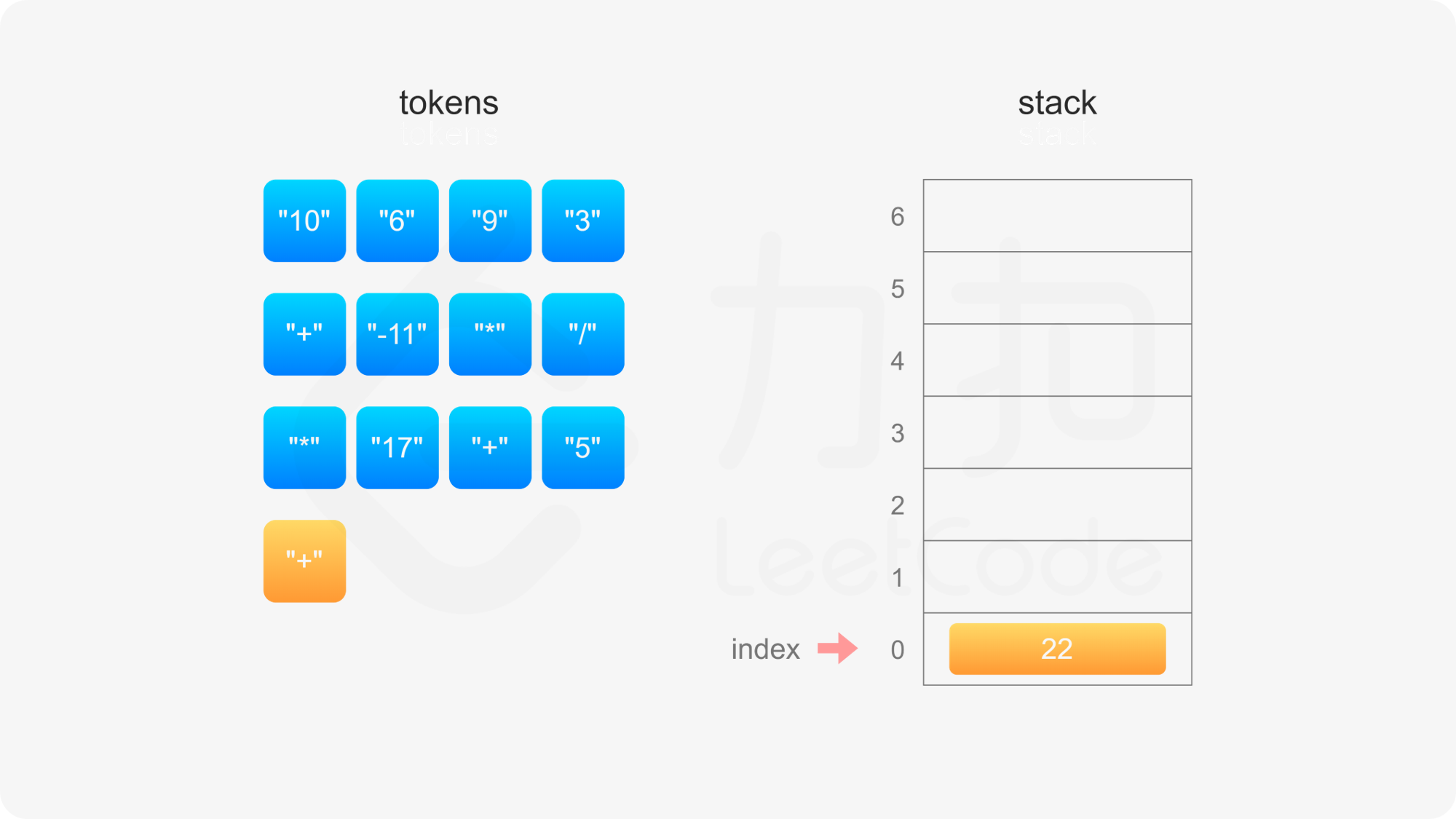
具体实现方面，创建数组 stack 模拟栈，数组下标 0 的位置对应栈底，定义 index 表示栈顶元素的下标位置，初始时栈为空，index}=-1。当遇到操作数和运算符时，进行如下操作：

  • 如果遇到操作数，则将 index 的值加 1，然后将操作数赋给 stack}[\textit{index}]；

  • 如果遇到运算符，则将 index 的值减 1，此时 stack}[\textit{index}] 和 stack}[\textit{index}+1] 的元素分别是左操作数和右操作数，使用运算符对两个操作数进行运算，将运算得到的新操作数赋给 stack}[\textit{index}]。

整个后缀表达式遍历完毕之后，栈内只有一个元素，因此 index}=0，此时 stack}[\textit{index}] 即为后缀表达式的值。

<ppt1,ppt2,ppt3,ppt4,ppt5,ppt6,ppt7,ppt8,ppt9,ppt10,ppt11,ppt12,ppt13,ppt14,ppt15>

[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int evalRPN(String[] tokens) {
        int n = tokens.length;
        int[] stack = new int[(n + 1) / 2];
        int index = -1;
        for (int i = 0; i < n; i++) {
            String token = tokens[i];
            switch (token) {
                case "+":
                    index--;
                    stack[index] += stack[index + 1];
                    break;
                case "-":
                    index--;
                    stack[index] -= stack[index + 1];
                    break;
                case "*":
                    index--;
                    stack[index] *= stack[index + 1];
                    break;
                case "/":
                    index--;
                    stack[index] /= stack[index + 1];
                    break;
                default:
                    index++;
                    stack[index] = Integer.parseInt(token);
            }
        }
        return stack[index];
    }
}
[sol2-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
var evalRPN = function(tokens) {
    const n = tokens.length;
    const stack = new Array(Math.floor((n + 1) / 2)).fill(0);
    let index = -1;
    for (let i = 0; i < n; i++) {
        const token = tokens[i];
        if (token === '+') {
            index--;
            stack[index] += stack[index + 1];
        } else if (token === '-') {
            index--;
            stack[index] -= stack[index + 1];
        } else if (token === '*') {
            index--;
            stack[index] *= stack[index + 1];
        } else if (token === '/') {
            index--;
            stack[index] = stack[index] / stack[index + 1] > 0 ? Math.floor(stack[index] / stack[index + 1]) : Math.ceil(stack[index] / stack[index + 1]);
        } else {
            index++;
            stack[index] = parseInt(token);
        }
    }
    return stack[index];
};
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func evalRPN(tokens []string) int {
    stack := make([]int, (len(tokens)+1)/2)
    index := -1
    for _, token := range tokens {
        val, err := strconv.Atoi(token)
        if err == nil {
            index++
            stack[index] = val
        } else {
            index--
            switch token {
            case "+":
                stack[index] += stack[index+1]
            case "-":
                stack[index] -= stack[index+1]
            case "*":
                stack[index] *= stack[index+1]
            default:
                stack[index] /= stack[index+1]
            }
        }
    }
    return stack[0]
}
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def evalRPN(self, tokens: List[str]) -> int:
        op_to_binary_fn = {
            "+": add,
            "-": sub,
            "*": mul,
            "/": lambda x, y: int(x / y),   # 需要注意 python 中负数除法的表现与题目不一致
        }

        n = len(tokens)
        stack = [0] * ((n + 1) // 2)
        index = -1
        for token in tokens:
            try:
                num = int(token)
                index += 1
                stack[index] = num
            except ValueError:
                index -= 1
                stack[index] = op_to_binary_fn[token](stack[index], stack[index + 1])
            
        return stack[0]
[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        int n = tokens.size();
        vector<int> stk((n + 1) / 2);
        int index = -1;
        for (int i = 0; i < n; i++) {
            string& token = tokens[i];
            if (token.length() > 1 || isdigit(token[0])) {
                index++;
                stk[index] = atoi(token.c_str());
            } else {
                switch (token[0]) {
                    case '+':
                        index--;
                        stk[index] += stk[index + 1];
                        break;
                    case '-':
                        index--;
                        stk[index] -= stk[index + 1];
                        break;
                    case '*':
                        index--;
                        stk[index] *= stk[index + 1];
                        break;
                    case '/':
                        index--;
                        stk[index] /= stk[index + 1];
                        break;
                }
            }
        }
        return stk[index];
    }
};
[sol2-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
int evalRPN(char** tokens, int tokensSize) {
    int n = tokensSize;
    int stk[(n + 1) / 2];
    memset(stk, 0, sizeof(stk));
    int index = -1;
    for (int i = 0; i < n; i++) {
        char* token = tokens[i];
        if (strlen(token) > 1 || isdigit(token[0])) {
            index++;
            stk[index] = atoi(token);
        } else {
            switch (token[0]) {
                case '+':
                    index--;
                    stk[index] += stk[index + 1];
                    break;
                case '-':
                    index--;
                    stk[index] -= stk[index + 1];
                    break;
                case '*':
                    index--;
                    stk[index] *= stk[index + 1];
                    break;
                case '/':
                    index--;
                    stk[index] /= stk[index + 1];
                    break;
            }
        }
    }
    return stk[index];
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 是数组 tokens 的长度。需要遍历数组 tokens 一次，计算后缀表达式的值。

  • 空间复杂度：O(n)，其中 n 是数组 tokens 的长度。需要创建长度为 n+1/2 的数组模拟栈操作。

 Comments
On this page
LCR 036-逆波兰表达式求值