给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:

**输入:** [1,2,3,null,5,null,4]
**输出:** [1,3,4]
示例 2:
**输入:** [1,null,3]
**输出:** [1,3]
示例 3:
**输入:** []
**输出:** []
提示:
- 二叉树的节点个数的范围是
[0,100]
-100 <= Node.val <= 100
注意:本题与主站 199 题相同:<https://leetcode-cn.com/problems/binary-tree-right-side-
view/>
前言
由于树的形状无法提前知晓,不可能设计出优于 O(n) 的算法。因此,我们应该试着寻找线性时间解。带着这个想法,我们来考虑一些同等有效的方案。
方法一:深度优先搜索
思路
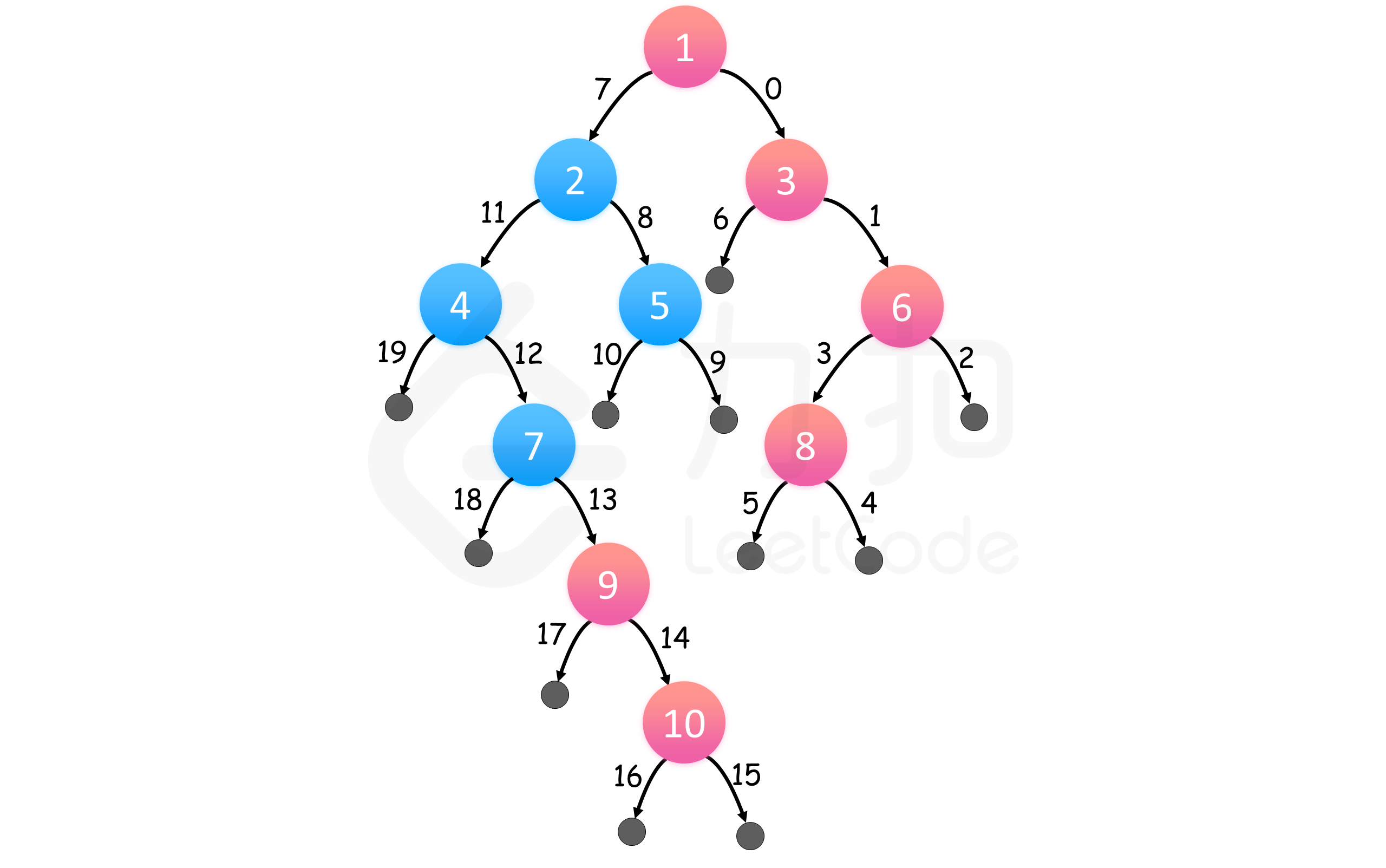
我们对树进行深度优先搜索,在搜索过程中,我们总是先访问右子树。那么对于每一层来说,我们在这层见到的第一个结点一定是最右边的结点。
算法
这样一来,我们可以存储在每个深度访问的第一个结点,一旦我们知道了树的层数,就可以得到最终的结果数组。

上图表示了问题的一个实例。红色结点自上而下组成答案,边缘以访问顺序标号。
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
rightmost_value_at_depth = dict()
max_depth = -1
stack = [(root, 0)]
while stack:
node, depth = stack.pop()
if node is not None:
max_depth = max(max_depth, depth)
rightmost_value_at_depth.setdefault(depth, node.val)
stack.append((node.left, depth + 1))
stack.append((node.right, depth + 1))
return [rightmost_value_at_depth[depth] for depth in range(max_depth + 1)]
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| class Solution {
public List<Integer> rightSideView(TreeNode root) {
Map<Integer, Integer> rightmostValueAtDepth = new HashMap<Integer, Integer>();
int max_depth = -1;
Deque<TreeNode> nodeStack = new LinkedList<TreeNode>();
Deque<Integer> depthStack = new LinkedList<Integer>();
nodeStack.push(root);
depthStack.push(0);
while (!nodeStack.isEmpty()) {
TreeNode node = nodeStack.pop();
int depth = depthStack.pop();
if (node != null) {
max_depth = Math.max(max_depth, depth);
if (!rightmostValueAtDepth.containsKey(depth)) {
rightmostValueAtDepth.put(depth, node.val);
}
nodeStack.push(node.left);
nodeStack.push(node.right);
depthStack.push(depth + 1);
depthStack.push(depth + 1);
}
}
List<Integer> rightView = new ArrayList<Integer>();
for (int depth = 0; depth <= max_depth; depth++) {
rightView.add(rightmostValueAtDepth.get(depth));
}
return rightView;
}
}
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
unordered_map<int, int> rightmostValueAtDepth;
int max_depth = -1;
stack<TreeNode*> nodeStack;
stack<int> depthStack;
nodeStack.push(root);
depthStack.push(0);
while (!nodeStack.empty()) {
TreeNode* node = nodeStack.top();nodeStack.pop();
int depth = depthStack.top();depthStack.pop();
if (node != NULL) {
max_depth = max(max_depth, depth);
if (rightmostValueAtDepth.find(depth) == rightmostValueAtDepth.end()) {
rightmostValueAtDepth[depth] = node -> val;
}
nodeStack.push(node -> left);
nodeStack.push(node -> right);
depthStack.push(depth + 1);
depthStack.push(depth + 1);
}
}
vector<int> rightView;
for (int depth = 0; depth <= max_depth; ++depth) {
rightView.push_back(rightmostValueAtDepth[depth]);
}
return rightView;
}
};
|
复杂度分析
方法二:广度优先搜索
思路
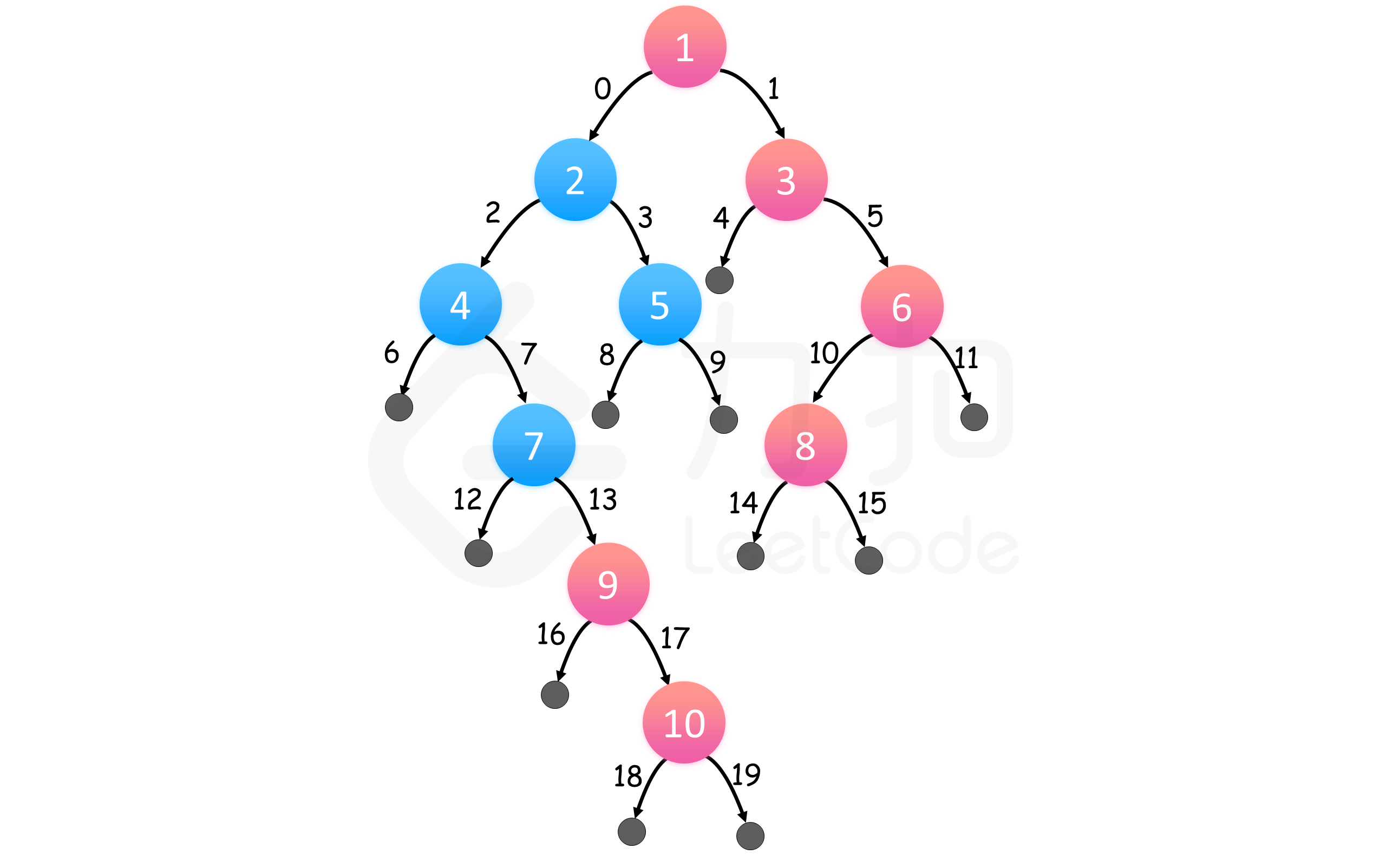
我们可以对二叉树进行层次遍历,那么对于每层来说,最右边的结点一定是最后被遍历到的。二叉树的层次遍历可以用广度优先搜索实现。
算法
执行广度优先搜索,左结点排在右结点之前,这样,我们对每一层都从左到右访问。因此,只保留每个深度最后访问的结点,我们就可以在遍历完整棵树后得到每个深度最右的结点。除了将栈改成队列,并去除了 rightmost_value_at_depth 之前的检查外,算法没有别的改动。

上图表示了同一个示例,红色结点自上而下组成答案,边缘以访问顺序标号。
[sol2-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
rightmost_value_at_depth = dict()
max_depth = -1
queue = deque([(root, 0)])
while queue:
node, depth = queue.popleft()
if node is not None:
max_depth = max(max_depth, depth)
rightmost_value_at_depth[depth] = node.val
queue.append((node.left, depth + 1))
queue.append((node.right, depth + 1))
return [rightmost_value_at_depth[depth] for depth in range(max_depth + 1)]
|
[sol2-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public List<Integer> rightSideView(TreeNode root) {
Map<Integer, Integer> rightmostValueAtDepth = new HashMap<Integer, Integer>();
int max_depth = -1;
Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();
Queue<Integer> depthQueue = new LinkedList<Integer>();
nodeQueue.add(root);
depthQueue.add(0);
while (!nodeQueue.isEmpty()) {
TreeNode node = nodeQueue.remove();
int depth = depthQueue.remove();
if (node != null) {
max_depth = Math.max(max_depth, depth);
rightmostValueAtDepth.put(depth, node.val);
nodeQueue.add(node.left);
nodeQueue.add(node.right);
depthQueue.add(depth + 1);
depthQueue.add(depth + 1);
}
}
List<Integer> rightView = new ArrayList<Integer>();
for (int depth = 0; depth <= max_depth; depth++) {
rightView.add(rightmostValueAtDepth.get(depth));
}
return rightView;
}
}
|
[sol2-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
unordered_map<int, int> rightmostValueAtDepth;
int max_depth = -1;
queue<TreeNode*> nodeQueue;
queue<int> depthQueue;
nodeQueue.push(root);
depthQueue.push(0);
while (!nodeQueue.empty()) {
TreeNode* node = nodeQueue.front();nodeQueue.pop();
int depth = depthQueue.front();depthQueue.pop();
if (node != NULL) {
max_depth = max(max_depth, depth);
rightmostValueAtDepth[depth] = node -> val;
nodeQueue.push(node -> left);
nodeQueue.push(node -> right);
depthQueue.push(depth + 1);
depthQueue.push(depth + 1);
}
}
vector<int> rightView;
for (int depth = 0; depth <= max_depth; ++depth) {
rightView.push_back(rightmostValueAtDepth[depth]);
}
return rightView;
}
};
|
复杂度分析
注释
deque 数据类型来自于collections 模块,支持从头和尾部的常数时间 append/pop 操作。若使用 Python 的 list,通过 list.pop(0) 去除头部会消耗 O(n) 的时间。