给定一个二叉树 根节点 root ,树的每个节点的值要么是 0,要么是 1。请剪除该二叉树中所有节点的值为 0 的子树。
节点 node 的子树为 node 本身,以及所有 node 的后代。
示例 1:
**输入:** [1,null,0,0,1]
**输出:** [1,null,0,null,1]
**解释:**
只有红色节点满足条件"所有不包含 1 的子树"。
右图为返回的答案。

示例 2:
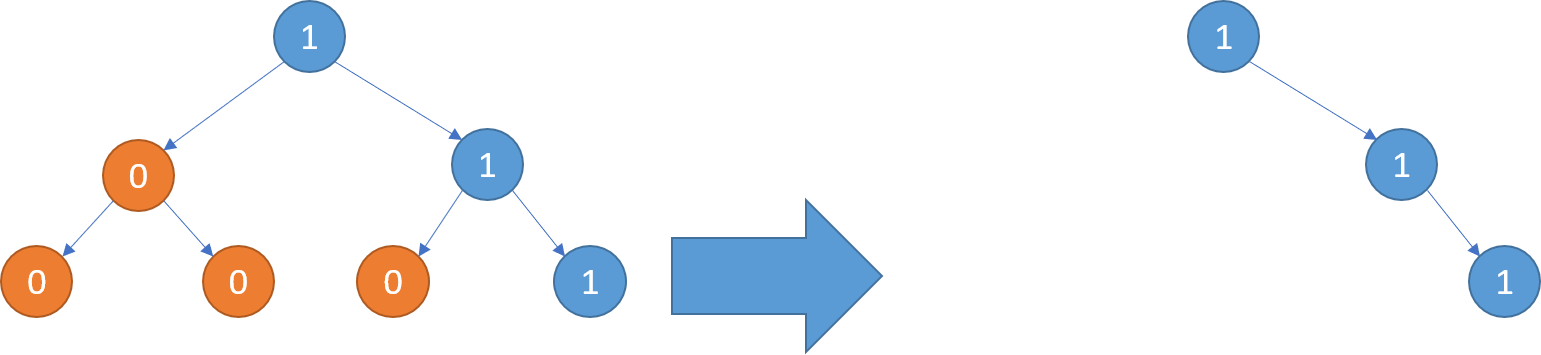
**输入:** [1,0,1,0,0,0,1]
**输出:** [1,null,1,null,1]
**解释:**
示例 3:
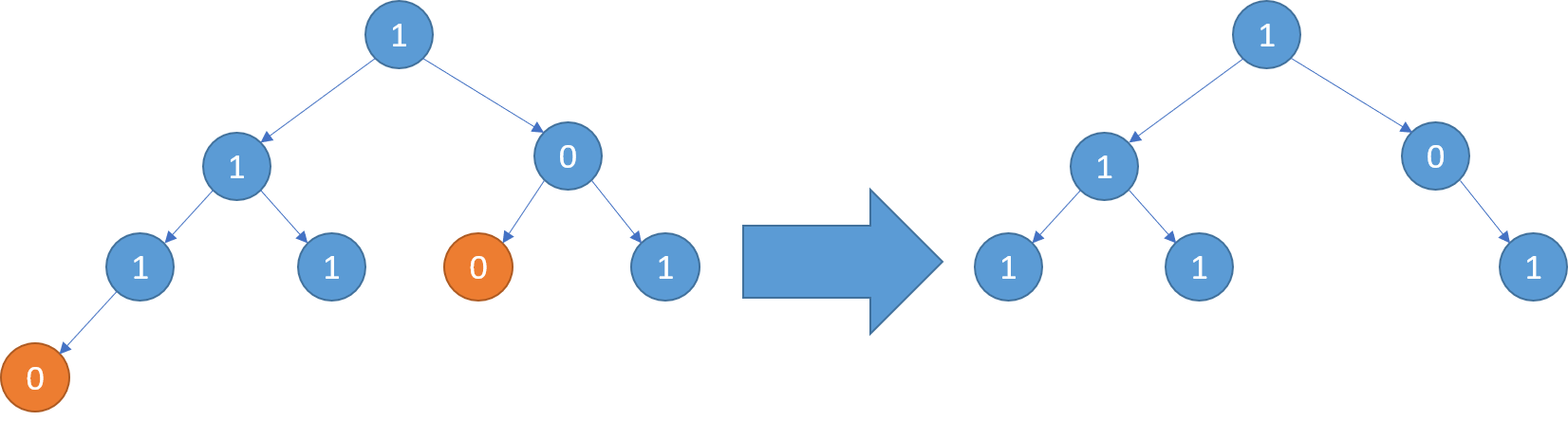
**输入:** [1,1,0,1,1,0,1,0]
**输出:** [1,1,0,1,1,null,1]
**解释:**
提示:
- 二叉树的节点个数的范围是
[1,200]
- 二叉树节点的值只会是
0 或 1
注意:本题与主站 814 题相同:https://leetcode-cn.com/problems/binary-tree-pruning/
方法一:递归
思路
树相关的题目首先考虑用递归解决。首先确定边界条件,当输入为空时,即可返回空。然后对左子树和右子树分别递归进行 pruneTree 操作。递归完成后,当这三个条件:左子树为空,右子树为空,当前节点的值为 0,同时满足时,才表示以当前节点为根的原二叉树的所有节点都为 0,需要将这棵子树移除,返回空。有任一条件不满足时,当前节点不应该移除,返回当前节点。
代码
[sol1-Python3]1
2
3
4
5
6
7
8
9
| class Solution:
def pruneTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if root is None:
return None
root.left = self.pruneTree(root.left)
root.right = self.pruneTree(root.right)
if root.left is None and root.right is None and root.val == 0:
return None
return root
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public TreeNode pruneTree(TreeNode root) {
if (root == null) {
return null;
}
root.left = pruneTree(root.left);
root.right = pruneTree(root.right);
if (root.left == null && root.right == null && root.val == 0) {
return null;
}
return root;
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
| public class Solution {
public TreeNode PruneTree(TreeNode root) {
if (root == null) {
return null;
}
root.left = PruneTree(root.left);
root.right = PruneTree(root.right);
if (root.left == null && root.right == null && root.val == 0) {
return null;
}
return root;
}
}
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public:
TreeNode* pruneTree(TreeNode* root) {
if (!root) {
return nullptr;
}
root->left = pruneTree(root->left);
root->right = pruneTree(root->right);
if (!root->left && !root->right && !root->val) {
return nullptr;
}
return root;
}
};
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
| struct TreeNode* pruneTree(struct TreeNode* root){
if (!root) {
return NULL;
}
root->left = pruneTree(root->left);
root->right = pruneTree(root->right);
if (!root->left && !root->right && !root->val) {
return NULL;
}
return root;
}
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
| func pruneTree(root *TreeNode) *TreeNode {
if root == nil {
return nil
}
root.Left = pruneTree(root.Left)
root.Right = pruneTree(root.Right)
if root.Left == nil && root.Right == nil && root.Val == 0 {
return nil
}
return root
}
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
| var pruneTree = function(root) {
if (!root) {
return null;
}
root.left = pruneTree(root.left);
root.right = pruneTree(root.right);
if (!root.left && !root.right&& root.val === 0) {
return null;
}
return root;
};
|
复杂度分析