LCR 101-分割等和子集

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 17:01:06 2023-09-13 17:01:06 Updated    

给定一个非空的正整数数组 nums ，请判断能否将这些数字分成元素和相等的两部分。

示例 1：

**输入：** nums = [1,5,11,5]
**输出：** true
**解释：** nums **** 可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

**输入：** nums = [1,2,3,5]
**输出：** false
**解释：** nums **** 不可以分为和相等的两部分

提示：

  • 1 <= nums.length <= 200
  • 1 <= nums[i] <= 100

注意：本题与主站 416 题相同： <https://leetcode-cn.com/problems/partition-equal-subset-
sum/>

前言

作者在这里希望读者认真阅读前言部分。

本题是经典的「NP 完全问题 」，也就是说，如果你发现了该问题的一个多项式算法 ，那么恭喜你证明出了 P=NP，可以期待一下图灵奖了。

正因如此，我们不应期望该问题有多项式时间复杂度的解法。我们能想到的，例如基于贪心算法的「将数组降序排序后，依次将每个元素添加至当前元素和较小的子集中」之类的方法都是错误的，可以轻松地举出反例。因此，我们必须尝试非多项式时间复杂度的算法，例如时间复杂度与元素大小相关的动态规划。

方法一：动态规划

思路与算法

这道题可以换一种表述：给定一个只包含正整数的非空数组 nums}[0]，判断是否可以从数组中选出一些数字，使得这些数字的和等于整个数组的元素和的一半。因此这个问题可以转换成「0-1 背包问题」。这道题与传统的「0-1 背包问题」的区别在于，传统的「0-1 背包问题」要求选取的物品的重量之和不能超过背包的总容量，这道题则要求选取的数字的和恰好等于整个数组的元素和的一半。类似于传统的「0-1 背包问题」，可以使用动态规划求解。

在使用动态规划求解之前，首先需要进行以下判断。

  • 根据数组的长度 n 判断数组是否可以被划分。如果 n<2，则不可能将数组分割成元素和相等的两个子集，因此直接返回 false。

  • 计算整个数组的元素和 sum 以及最大元素 maxNum。如果 sum 是奇数，则不可能将数组分割成元素和相等的两个子集，因此直接返回 false。如果 sum 是偶数，则令 target}=\textit{sum} }{2，需要判断是否可以从数组中选出一些数字，使得这些数字的和等于 target。如果 maxNum}>\textit{target，则除了 maxNum 以外的所有元素之和一定小于 target，因此不可能将数组分割成元素和相等的两个子集，直接返回 false。

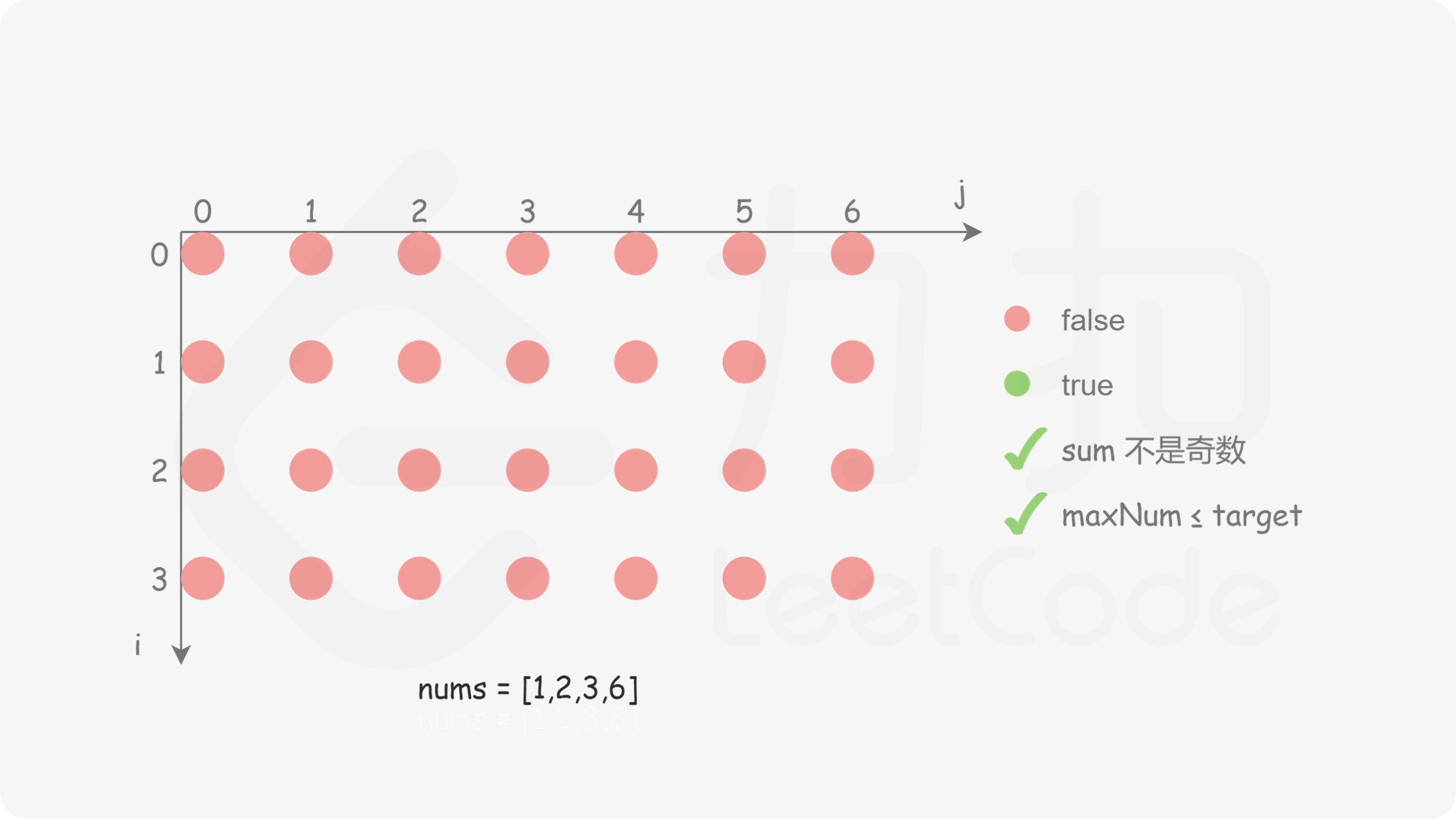
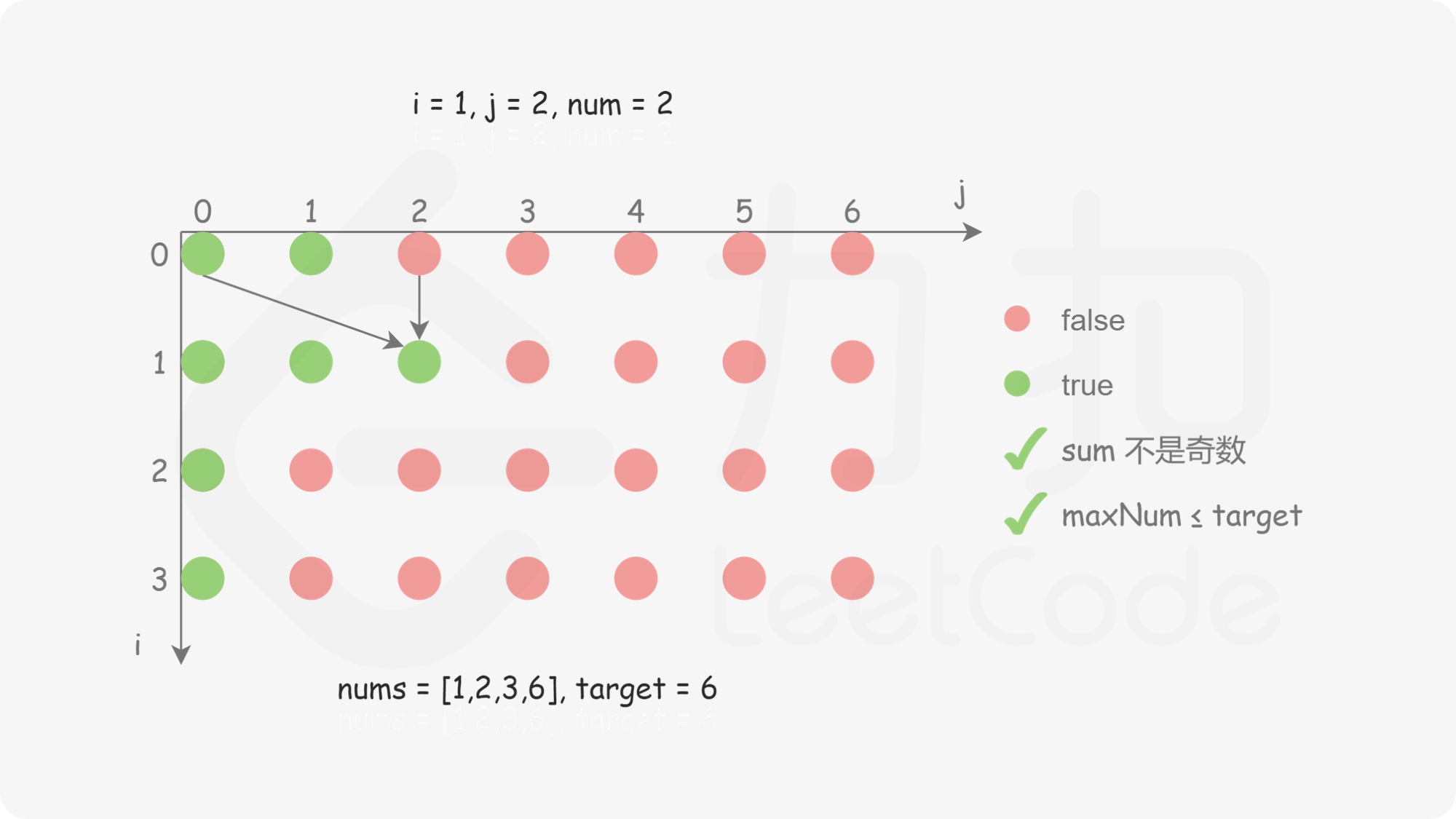
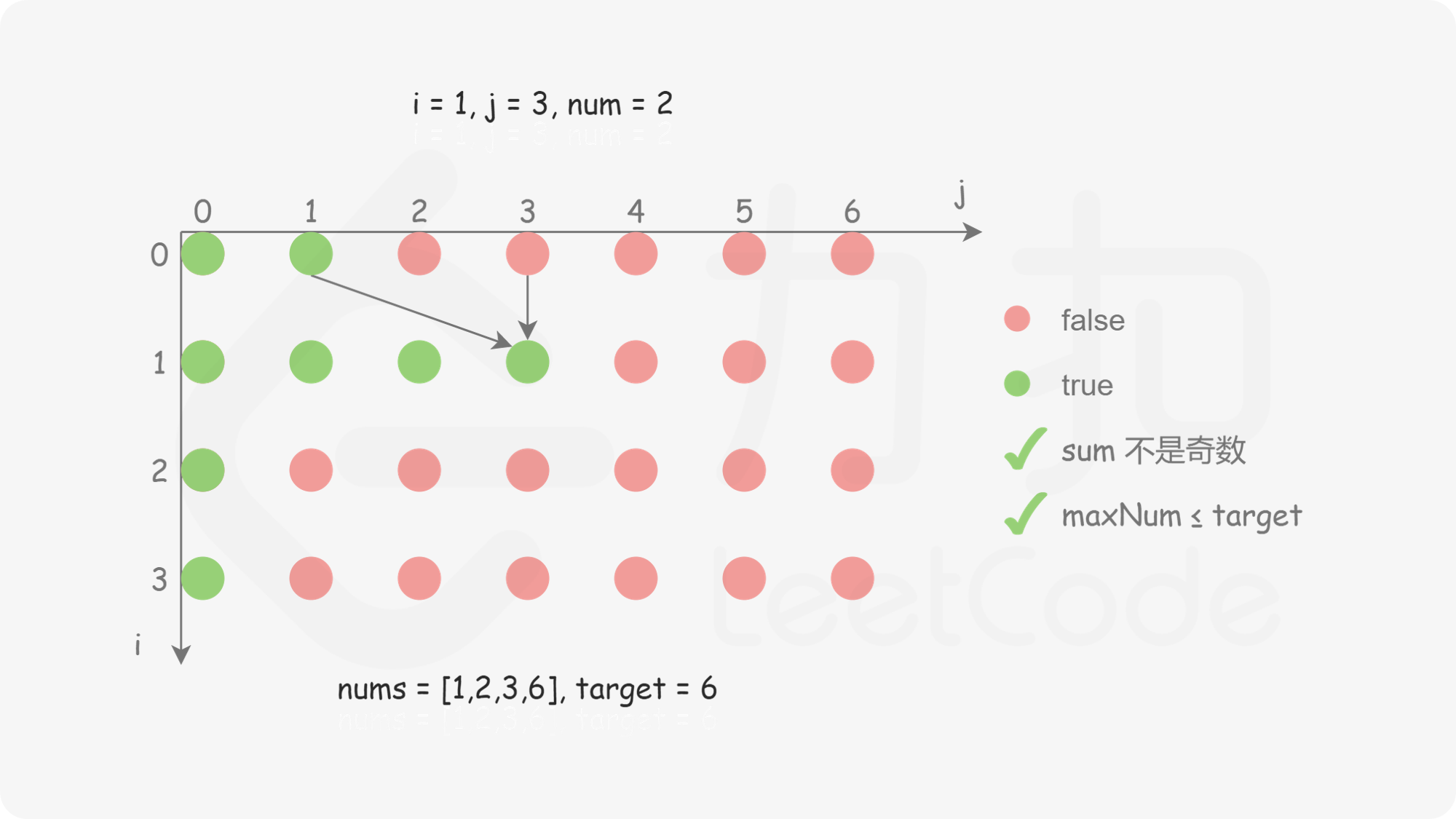
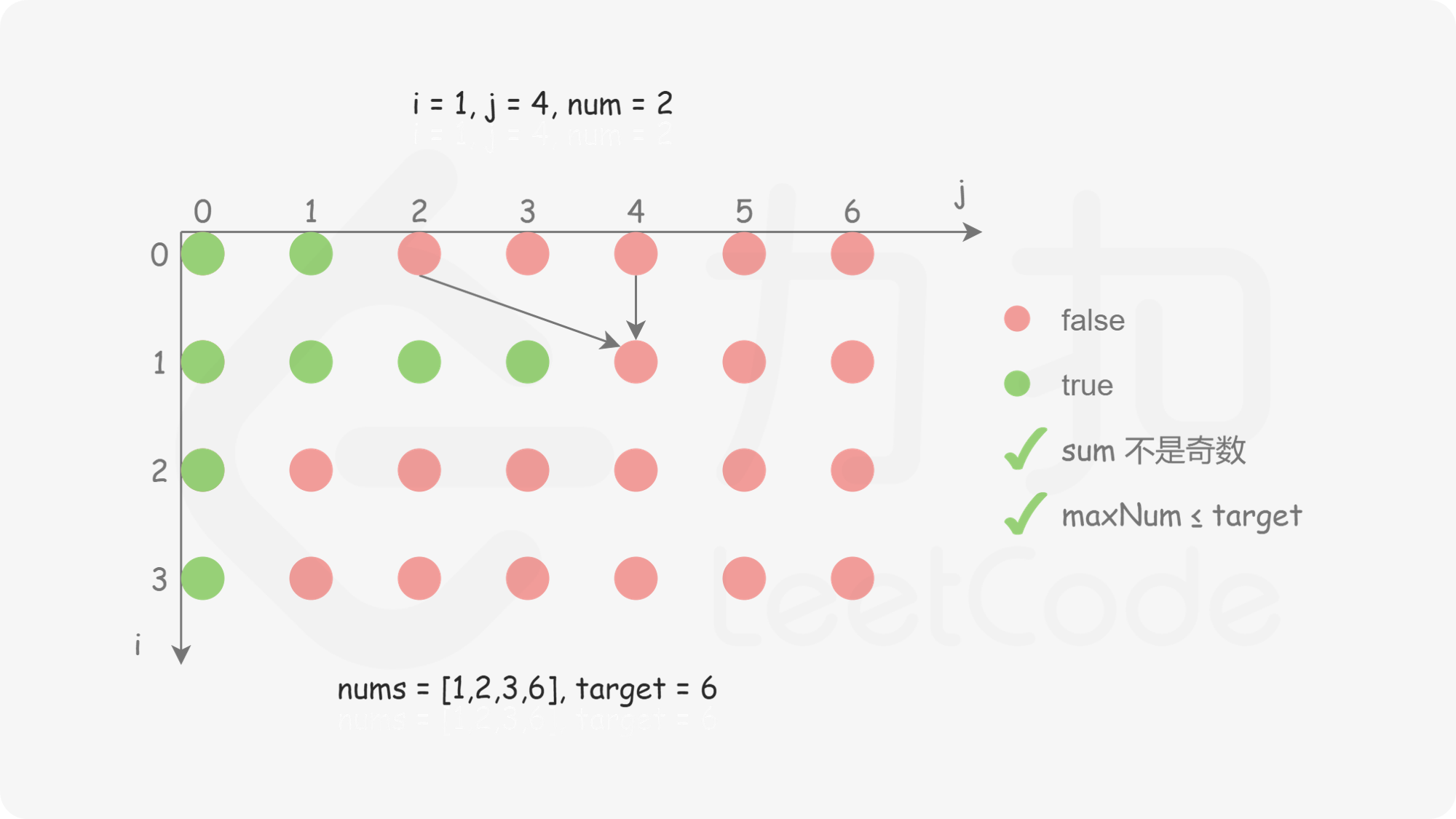
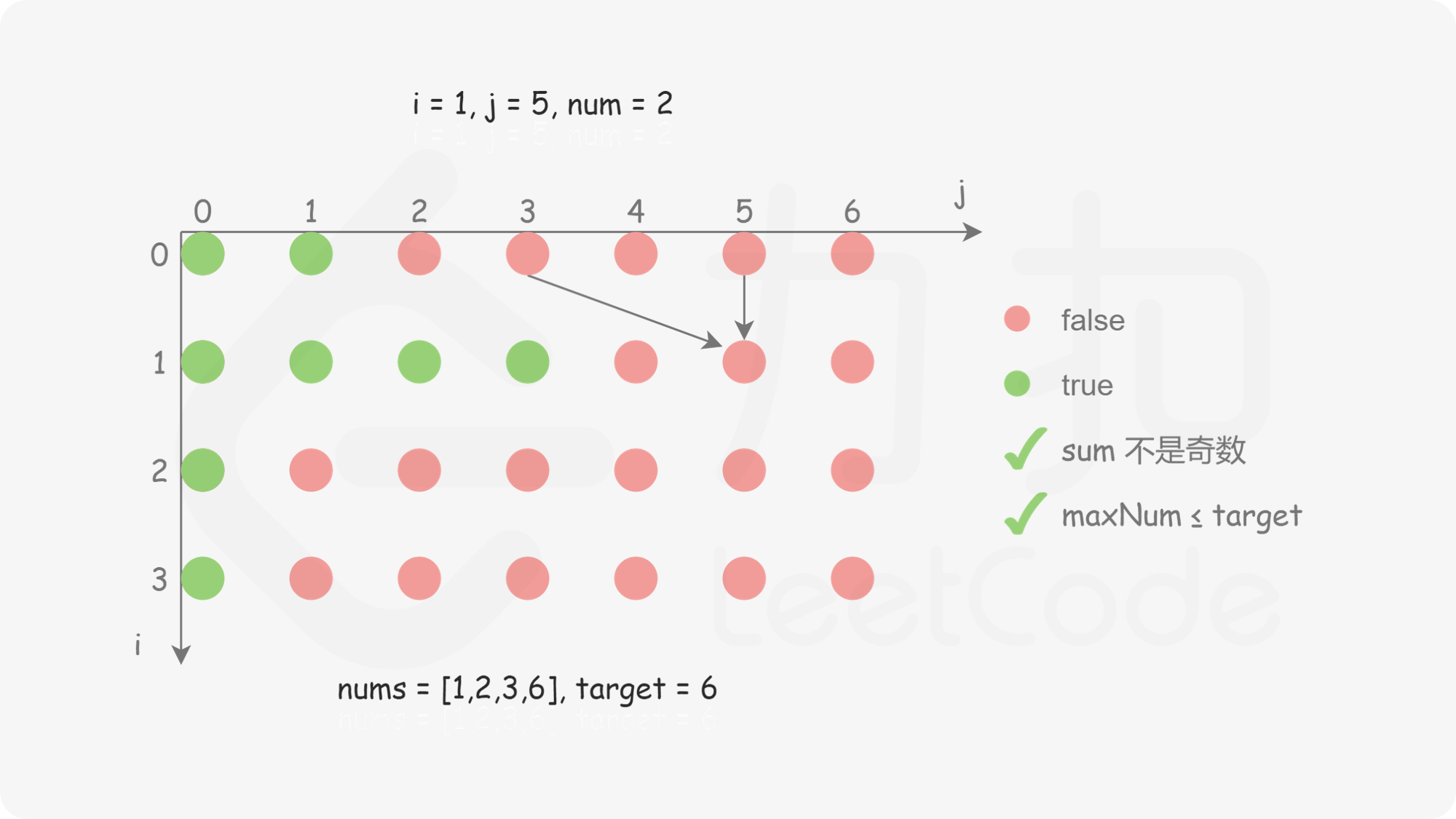
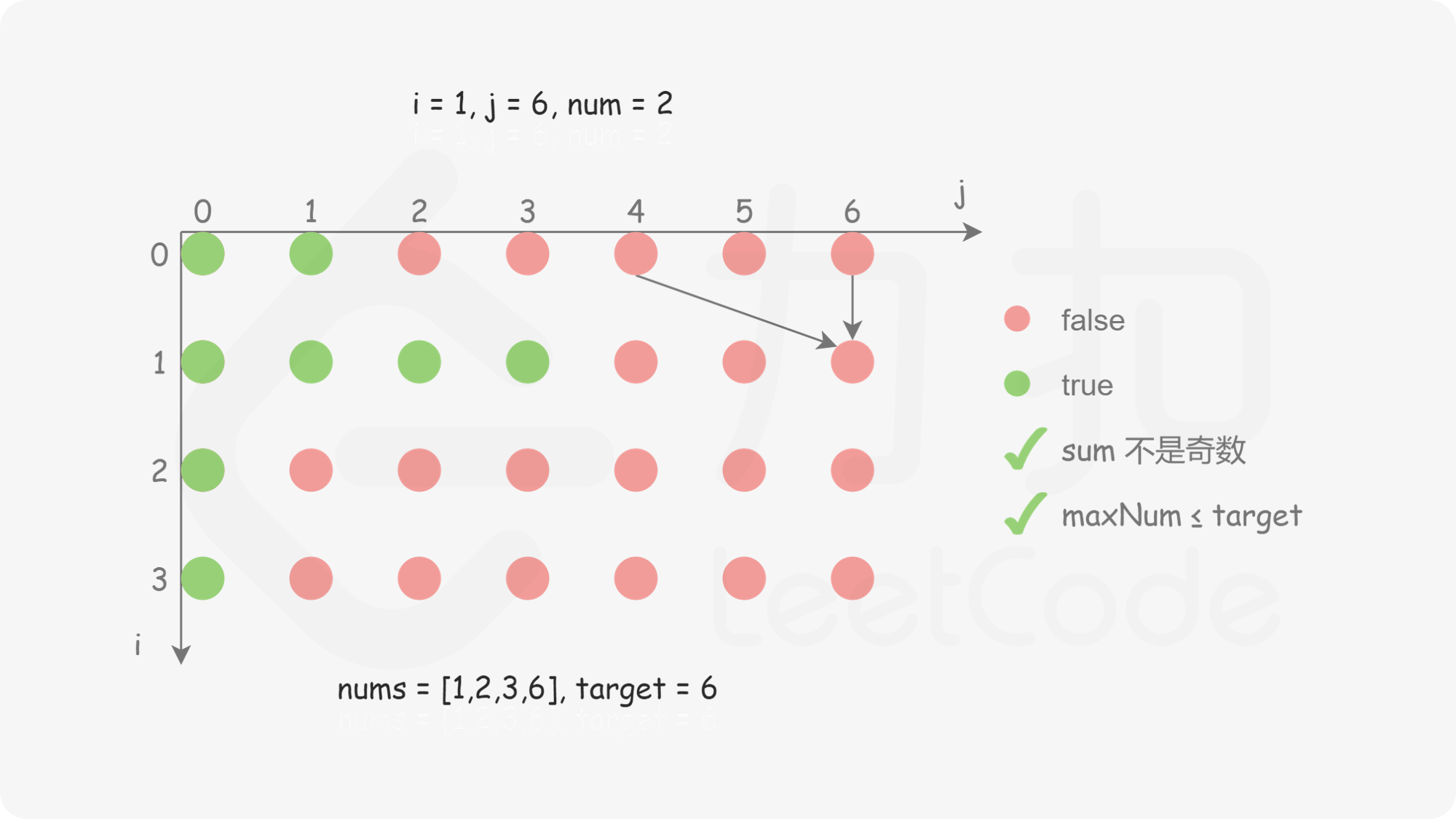
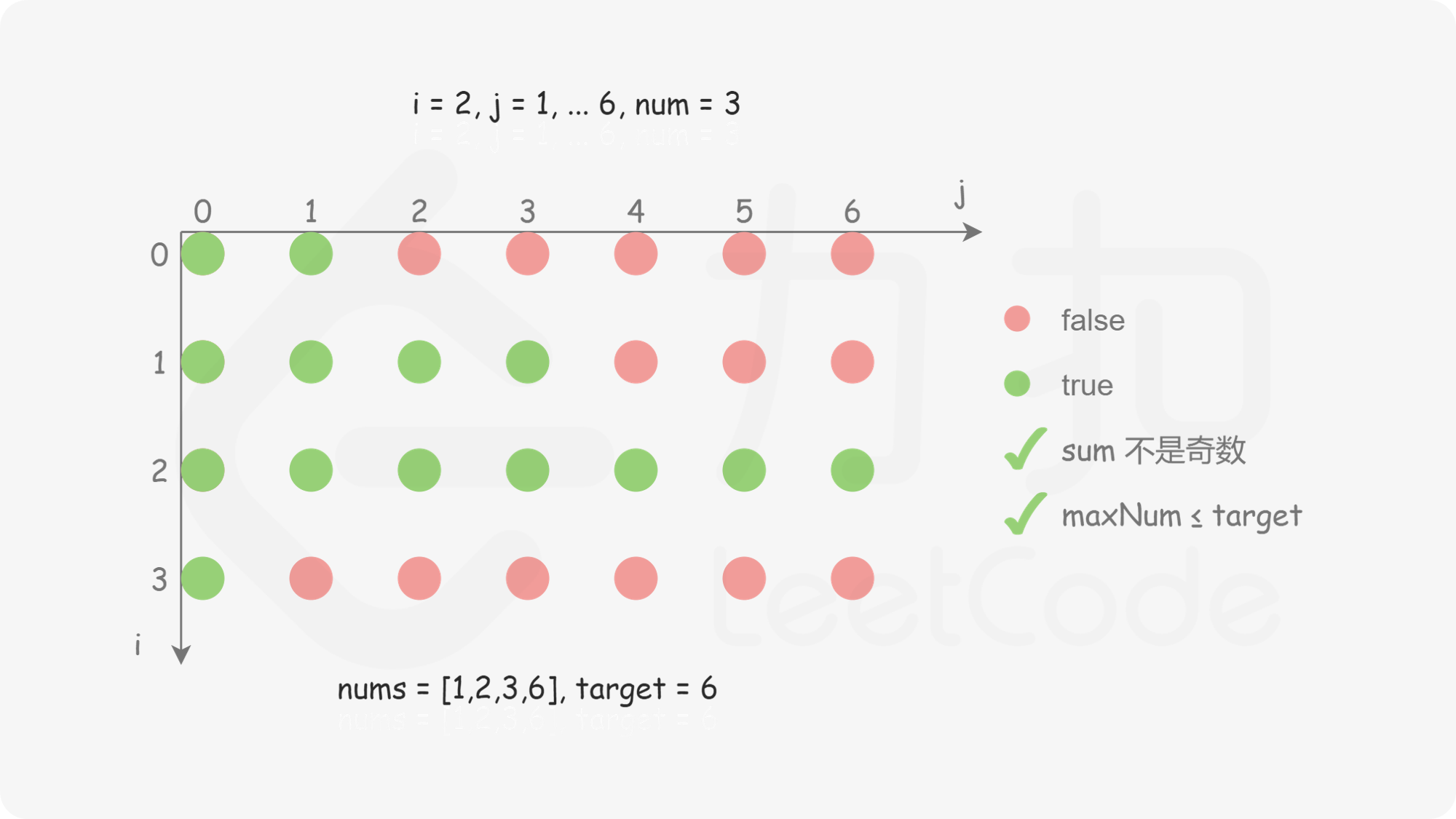
创建二维数组 dp，包含 n 行 target}+1 列，其中 dp}[i][j] 表示从数组的 [0,i] 下标范围内选取若干个正整数（可以是 0 个），是否存在一种选取方案使得被选取的正整数的和等于 j。初始时，dp 中的全部元素都是 false。

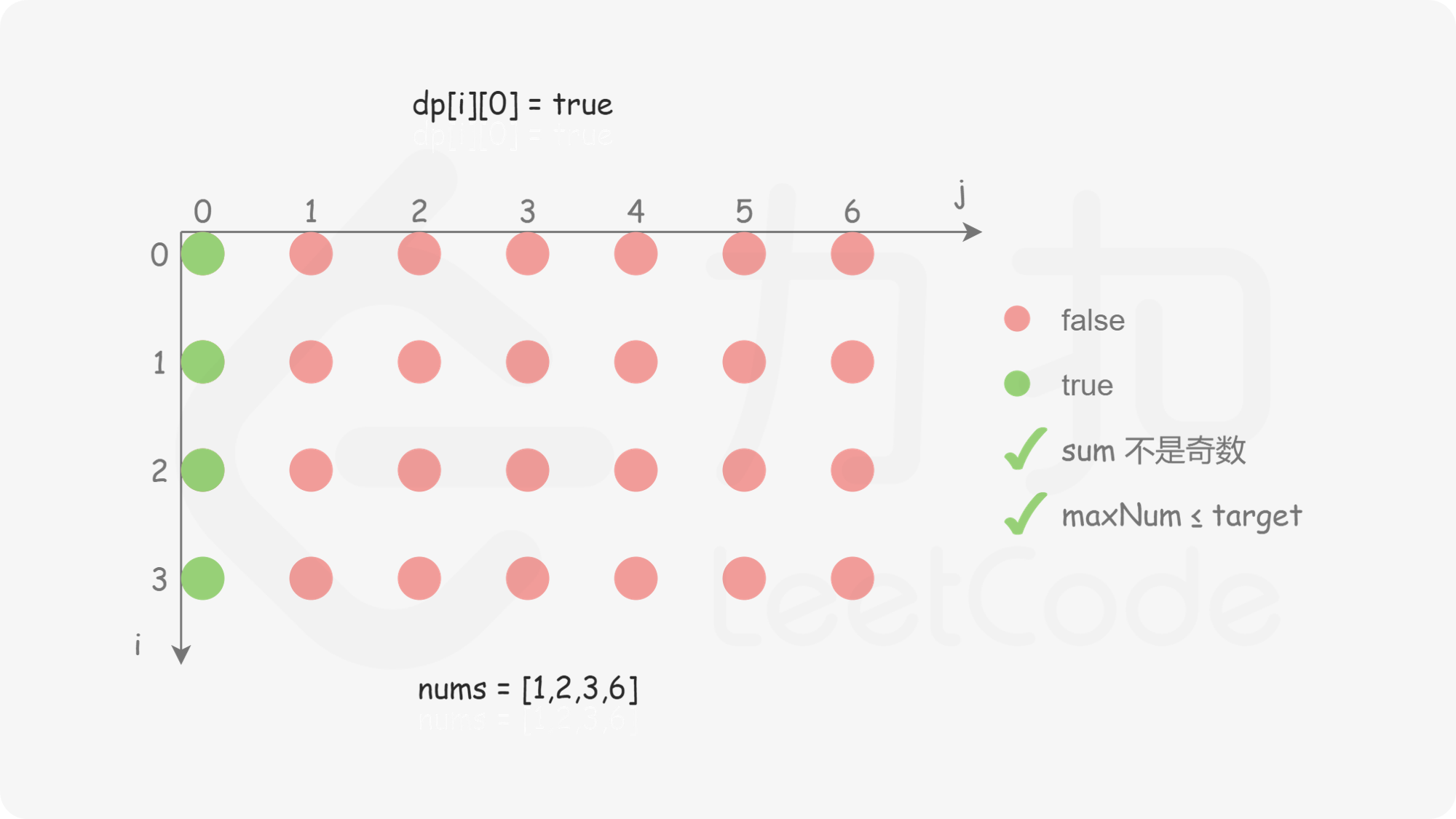
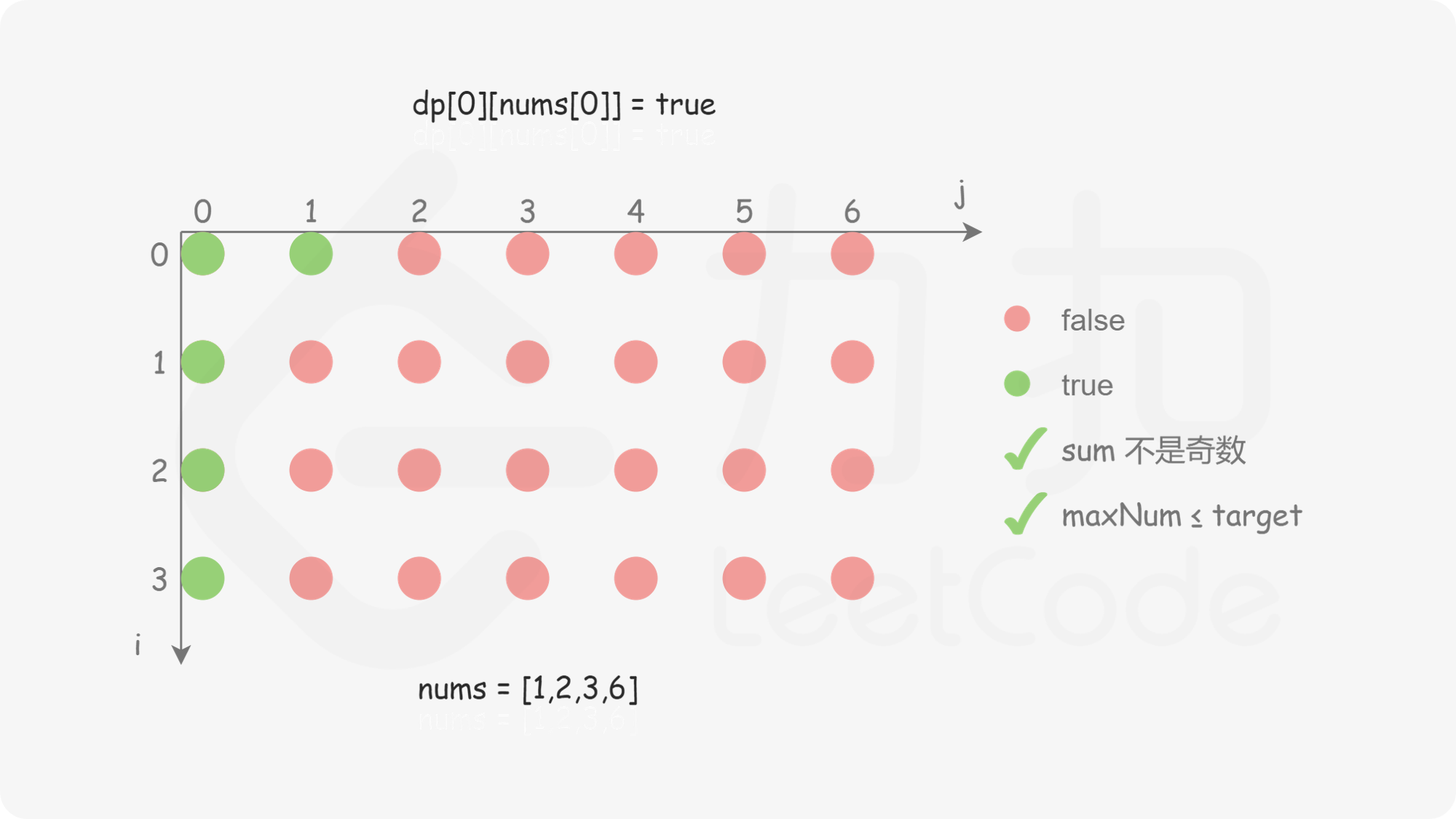
在定义状态之后，需要考虑边界情况。以下两种情况都属于边界情况。

  • 如果不选取任何正整数，则被选取的正整数等于 0。因此对于所有 0 \le i < n，都有 dp}[i][0]=\text{true。

  • 当 i==0 时，只有一个正整数 nums}[0] 可以被选取，因此 dp}[0][\textit{nums}[0]]=\text{true。

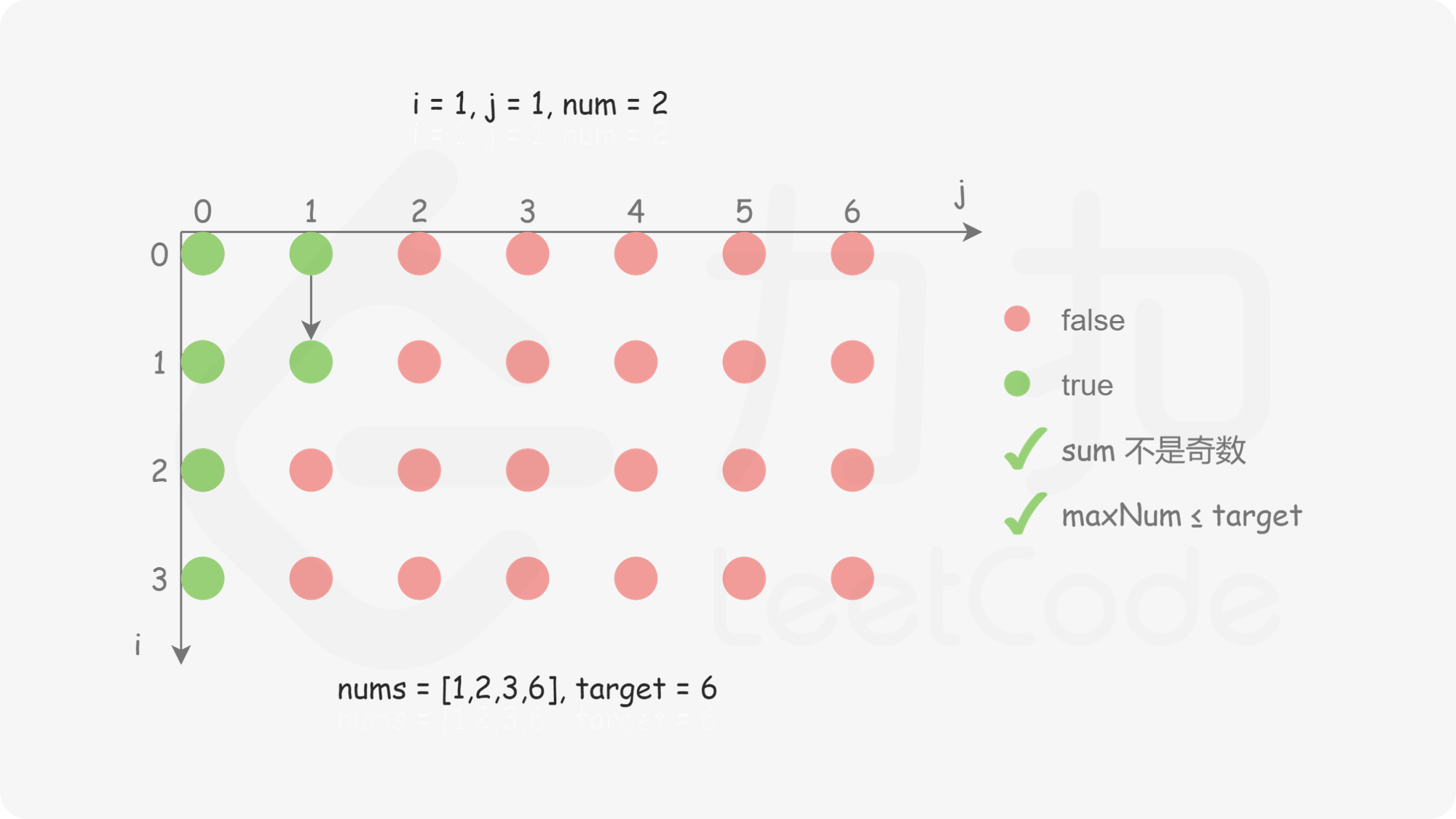
对于 i>0 且 j>0 的情况，如何确定 dp}[i][j] 的值？需要分别考虑以下两种情况。

  • 如果 j \ge \textit{nums}[i]，则对于当前的数字 nums}[i]，可以选取也可以不选取，两种情况只要有一个为 true，就有 dp}[i][j]=\text{true。

    • 如果不选取 nums}[i]，则 dp}[i][j]=\textit{dp}[i-1][j]；
    • 如果选取 nums}[i]，则 dp}[i][j]=\textit{dp}[i-1][j-\textit{nums}[i]]。

  • 如果 j < \textit{nums}[i]，则在选取的数字的和等于 j 的情况下无法选取当前的数字 nums}[i]，因此有 dp}[i][j]=\textit{dp}[i-1][j]。

状态转移方程如下：

\textit{dp}[i][j]=\begin{cases}
\textit{dp}[i-1][j]|\textit{dp}[i-1][j-\textit{nums}[i]], & j \ge \textit{nums}[i] \
\textit{dp}[i-1][j], & j < \textit{nums}[i]
\end{cases}

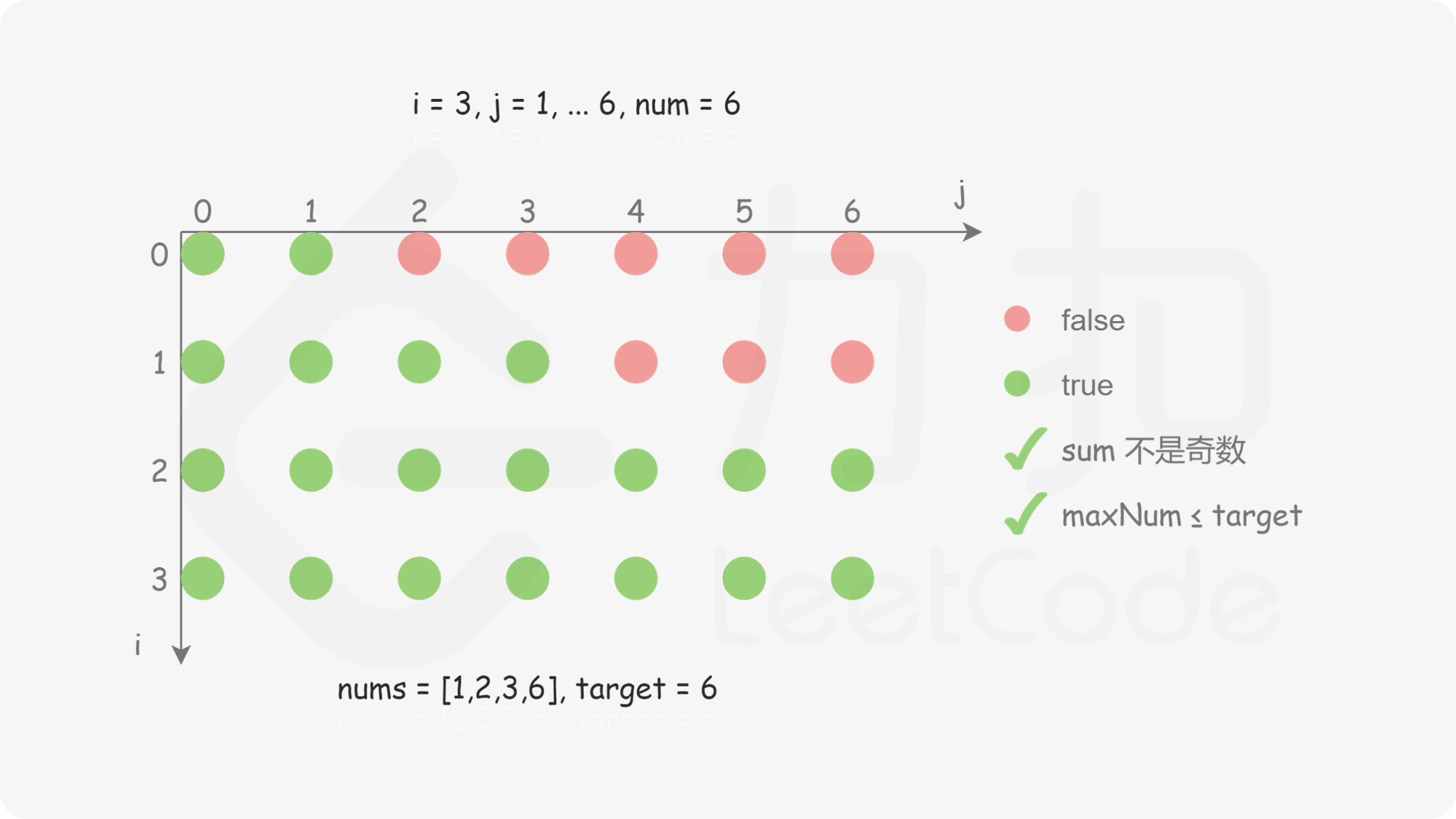
最终得到 dp}[n-1][\textit{target}] 即为答案。

<ppt1,ppt2,ppt3,ppt4,ppt5,ppt6,ppt7,ppt8,ppt9,ppt10,ppt11,ppt12>

[sol0-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    public boolean canPartition(int[] nums) {
        int n = nums.length;
        if (n < 2) {
            return false;
        }
        int sum = 0, maxNum = 0;
        for (int num : nums) {
            sum += num;
            maxNum = Math.max(maxNum, num);
        }
        if (sum % 2 != 0) {
            return false;
        }
        int target = sum / 2;
        if (maxNum > target) {
            return false;
        }
        boolean[][] dp = new boolean[n][target + 1];
        for (int i = 0; i < n; i++) {
            dp[i][0] = true;
        }
        dp[0][nums[0]] = true;
        for (int i = 1; i < n; i++) {
            int num = nums[i];
            for (int j = 1; j <= target; j++) {
                if (j >= num) {
                    dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[n - 1][target];
    }
}
[sol0-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int n = nums.size();
        if (n < 2) {
            return false;
        }
        int sum = accumulate(nums.begin(), nums.end(), 0);
        int maxNum = *max_element(nums.begin(), nums.end());
        if (sum & 1) {
            return false;
        }
        int target = sum / 2;
        if (maxNum > target) {
            return false;
        }
        vector<vector<int>> dp(n, vector<int>(target + 1, 0));
        for (int i = 0; i < n; i++) {
            dp[i][0] = true;
        }
        dp[0][nums[0]] = true;
        for (int i = 1; i < n; i++) {
            int num = nums[i];
            for (int j = 1; j <= target; j++) {
                if (j >= num) {
                    dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[n - 1][target];
    }
};
[sol0-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
var canPartition = function(nums) {
    const n = nums.length;
    if (n < 2) {
        return false;
    }
    let sum = 0, maxNum = 0;
    for (const num of nums) {
        sum += num;
        maxNum = maxNum > num ? maxNum : num;
    }
    if (sum & 1) {
        return false;
    }
    const target = Math.floor(sum / 2);
    if (maxNum > target) {
        return false;
    }
    const dp = new Array(n).fill(0).map(v => new Array(target + 1, false));
    for (let i = 0; i < n; i++) {
        dp[i][0] = true;
    }
    dp[0][nums[0]] = true;
    for (let i = 1; i < n; i++) {
        const num = nums[i];
        for (let j = 1; j <= target; j++) {
            if (j >= num) {
                dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num];
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    return dp[n - 1][target];
};
[sol0-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
func canPartition(nums []int) bool {
    n := len(nums)
    if n < 2 {
        return false
    }

    sum, max := 0, 0
    for _, v := range nums {
        sum += v
        if v > max {
            max = v
        }
    }
    if sum%2 != 0 {
        return false
    }

    target := sum / 2
    if max > target {
        return false
    }

    dp := make([][]bool, n)
    for i := range dp {
        dp[i] = make([]bool, target+1)
    }
    for i := 0; i < n; i++ {
        dp[i][0] = true
    }
    dp[0][nums[0]] = true
    for i := 1; i < n; i++ {
        v := nums[i]
        for j := 1; j <= target; j++ {
            if j >= v {
                dp[i][j] = dp[i-1][j] || dp[i-1][j-v]
            } else {
                dp[i][j] = dp[i-1][j]
            }
        }
    }
    return dp[n-1][target]
}
[sol0-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
bool canPartition(int* nums, int numsSize) {
    if (numsSize < 2) {
        return false;
    }
    int sum = 0, maxNum = 0;
    for (int i = 0; i < numsSize; ++i) {
        sum += nums[i];
        maxNum = fmax(maxNum, nums[i]);
    }
    if (sum & 1) {
        return false;
    }
    int target = sum / 2;
    if (maxNum > target) {
        return false;
    }
    int dp[numsSize][target + 1];
    memset(dp, 0, sizeof(dp));
    for (int i = 0; i < numsSize; i++) {
        dp[i][0] = true;
    }
    dp[0][nums[0]] = true;
    for (int i = 1; i < numsSize; i++) {
        int num = nums[i];
        for (int j = 1; j <= target; j++) {
            if (j >= num) {
                dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num];
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    return dp[numsSize - 1][target];
}
[sol0-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        n = len(nums)
        if n < 2:
            return False
        
        total = sum(nums)
        maxNum = max(nums)
        if total & 1:
            return False
        
        target = total // 2
        if maxNum > target:
            return False
        
        dp = [[False] * (target + 1) for _ in range(n)]
        for i in range(n):
            dp[i][0] = True
        
        dp[0][nums[0]] = True
        for i in range(1, n):
            num = nums[i]
            for j in range(1, target + 1):
                if j >= num:
                    dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num]
                else:
                    dp[i][j] = dp[i - 1][j]
        
        return dp[n - 1][target]

上述代码的空间复杂度是 O(n \times \textit{target})。但是可以发现在计算 dp 的过程中，每一行的 dp 值都只与上一行的 dp 值有关，因此只需要一个一维数组即可将空间复杂度降到 O(\textit{target})。此时的转移方程为：

\textit{dp}[j]=\textit{dp}[j]\ |\ dp[j-\textit{nums}[i]]

且需要注意的是第二层的循环我们需要从大到小计算，因为如果我们从小到大更新 dp 值，那么在计算 dp}[j] 值的时候，dp}[j-\textit{nums}[i]] 已经是被更新过的状态，不再是上一行的 dp 值。

代码

[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public boolean canPartition(int[] nums) {
        int n = nums.length;
        if (n < 2) {
            return false;
        }
        int sum = 0, maxNum = 0;
        for (int num : nums) {
            sum += num;
            maxNum = Math.max(maxNum, num);
        }
        if (sum % 2 != 0) {
            return false;
        }
        int target = sum / 2;
        if (maxNum > target) {
            return false;
        }
        boolean[] dp = new boolean[target + 1];
        dp[0] = true;
        for (int i = 0; i < n; i++) {
            int num = nums[i];
            for (int j = target; j >= num; --j) {
                dp[j] |= dp[j - num];
            }
        }
        return dp[target];
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int n = nums.size();
        if (n < 2) {
            return false;
        }
        int sum = 0, maxNum = 0;
        for (auto& num : nums) {
            sum += num;
            maxNum = max(maxNum, num);
        }
        if (sum & 1) {
            return false;
        }
        int target = sum / 2;
        if (maxNum > target) {
            return false;
        }
        vector<int> dp(target + 1, 0);
        dp[0] = true;
        for (int i = 0; i < n; i++) {
            int num = nums[i];
            for (int j = target; j >= num; --j) {
                dp[j] |= dp[j - num];
            }
        }
        return dp[target];
    }
};
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
var canPartition = function(nums) {
    const n = nums.length;
    if (n < 2) {
        return false;
    }
    let sum = 0, maxNum = 0;
    for (const num of nums) {
        sum += num;
        maxNum = maxNum > num ? maxNum : num;
    }
    if (sum & 1) {
        return false;
    }
    const target = Math.floor(sum / 2);
    if (maxNum > target) {
        return false;
    }
    const dp = new Array(target + 1).fill(false);
    dp[0] = true;
    for (const num of nums) {
        for (let j = target; j >= num; --j) {
            dp[j] |= dp[j - num];
        }
    }
    return dp[target];
};
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func canPartition(nums []int) bool {
    n := len(nums)
    if n < 2 {
        return false
    }

    sum, max := 0, 0
    for _, v := range nums {
        sum += v
        if v > max {
            max = v
        }
    }
    if sum%2 != 0 {
        return false
    }

    target := sum / 2
    if max > target {
        return false
    }

    dp := make([]bool, target+1)
    dp[0] = true
    for i := 0; i < n; i++ {
        v := nums[i]
        for j := target; j >= v; j-- {
            dp[j] = dp[j] || dp[j-v]
        }
    }
    return dp[target]
}
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
bool canPartition(int* nums, int numsSize) {
    if (numsSize < 2) {
        return false;
    }
    int sum = 0, maxNum = 0;
    for (int i = 0; i < numsSize; ++i) {
        sum += nums[i];
        maxNum = fmax(maxNum, nums[i]);
    }
    if (sum & 1) {
        return false;
    }
    int target = sum / 2;
    if (maxNum > target) {
        return false;
    }
    int dp[target + 1];
    memset(dp, 0, sizeof(dp));
    dp[0] = true;
    for (int i = 0; i < numsSize; i++) {
        int num = nums[i];
        for (int j = target; j >= num; --j) {
            dp[j] |= dp[j - num];
        }
    }
    return dp[target];
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        n = len(nums)
        if n < 2:
            return False
        
        total = sum(nums)
        if total % 2 != 0:
            return False
        
        target = total // 2
        dp = [True] + [False] * target
        for i, num in enumerate(nums):
            for j in range(target, num - 1, -1):
                dp[j] |= dp[j - num]
        
        return dp[target]

复杂度分析

  • 时间复杂度：O(n \times \textit{target})，其中 n 是数组的长度，target 是整个数组的元素和的一半。需要计算出所有的状态，每个状态在进行转移时的时间复杂度为 O(1)。

  • 空间复杂度：O(\textit{target})，其中 target 是整个数组的元素和的一半。空间复杂度取决于 dp 数组，在不进行空间优化的情况下，空间复杂度是 O(n \times \textit{target})，在进行空间优化的情况下，空间复杂度可以降到 O(\textit{target})。

 Comments
On this page
LCR 101-分割等和子集