LCR 105-岛屿的最大面积

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:29 2023-09-13 16:06:29 Updated    

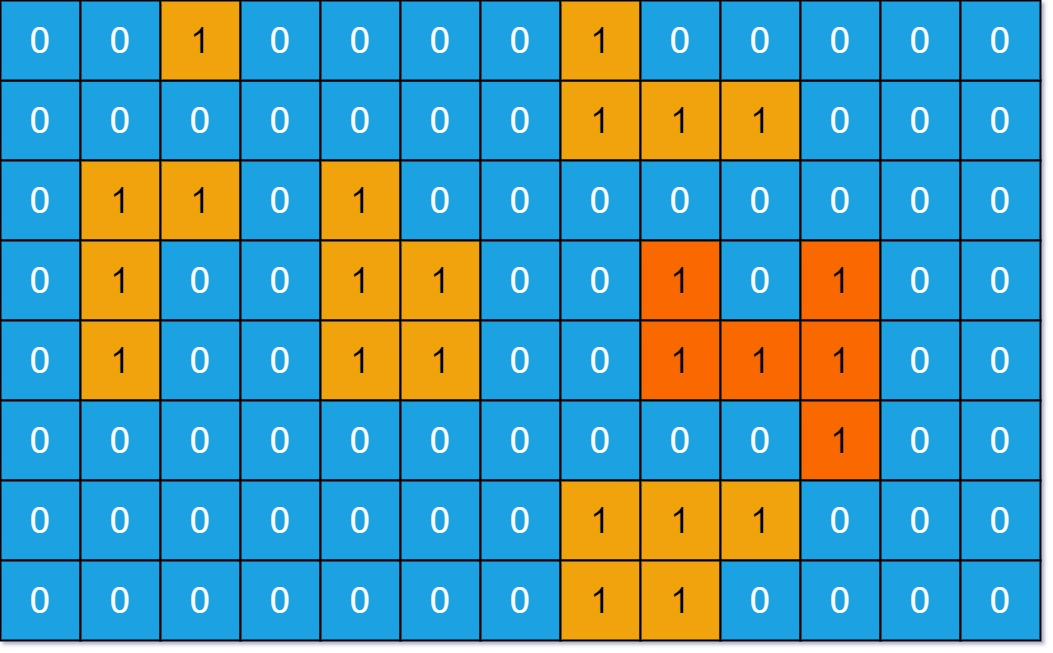
给定一个由 0 和 1 组成的非空二维数组 grid ，用来表示海洋岛屿地图。

一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设
grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1:

**输入:** grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
**输出:** 6
**解释:** 对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

示例 2:

**输入:** grid = [[0,0,0,0,0,0,0,0]]
**输出:** 0

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 50
  • grid[i][j] is either 0 or 1

注意：本题与主站 695 题相同： https://leetcode-cn.com/problems/max-area-of-island/

方法一：深度优先搜索

算法

  • 我们想知道网格中每个连通形状的面积，然后取最大值。

  • 如果我们在一个土地上，以 4 个方向探索与之相连的每一个土地（以及与这些土地相连的土地），那么探索过的土地总数将是该连通形状的面积。

  • 为了确保每个土地访问不超过一次，我们每次经过一块土地时，将这块土地的值置为 0。这样我们就不会多次访问同一土地。

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def dfs(self, grid, cur_i, cur_j) -> int:
        if cur_i < 0 or cur_j < 0 or cur_i == len(grid) or cur_j == len(grid[0]) or grid[cur_i][cur_j] != 1:
            return 0
        grid[cur_i][cur_j] = 0
        ans = 1
        for di, dj in [[0, 1], [0, -1], [1, 0], [-1, 0]]:
            next_i, next_j = cur_i + di, cur_j + dj
            ans += self.dfs(grid, next_i, next_j)
        return ans

    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        ans = 0
        for i, l in enumerate(grid):
            for j, n in enumerate(l):
                ans = max(self.dfs(grid, i, j), ans)
        return ans

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    int dfs(vector<vector<int>>& grid, int cur_i, int cur_j) {
        if (cur_i < 0 || cur_j < 0 || cur_i == grid.size() || cur_j == grid[0].size() || grid[cur_i][cur_j] != 1) {
            return 0;
        }
        grid[cur_i][cur_j] = 0;
        int di[4] = {0, 0, 1, -1};
        int dj[4] = {1, -1, 0, 0};
        int ans = 1;
        for (int index = 0; index != 4; ++index) {
            int next_i = cur_i + di[index], next_j = cur_j + dj[index];
            ans += dfs(grid, next_i, next_j);
        }
        return ans;
    }
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int ans = 0;
        for (int i = 0; i != grid.size(); ++i) {
            for (int j = 0; j != grid[0].size(); ++j) {
                ans = max(ans, dfs(grid, i, j));
            }
        }
        return ans;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        int ans = 0;
        for (int i = 0; i != grid.length; ++i) {
            for (int j = 0; j != grid[0].length; ++j) {
                ans = Math.max(ans, dfs(grid, i, j));
            }
        }
        return ans;
    }

    public int dfs(int[][] grid, int cur_i, int cur_j) {
        if (cur_i < 0 || cur_j < 0 || cur_i == grid.length || cur_j == grid[0].length || grid[cur_i][cur_j] != 1) {
            return 0;
        }
        grid[cur_i][cur_j] = 0;
        int[] di = {0, 0, 1, -1};
        int[] dj = {1, -1, 0, 0};
        int ans = 1;
        for (int index = 0; index != 4; ++index) {
            int next_i = cur_i + di[index], next_j = cur_j + dj[index];
            ans += dfs(grid, next_i, next_j);
        }
        return ans;
    }
}

复杂度分析

  • 时间复杂度：O(m \times n)。其中 m 是给定网格中的行数，n 是列数。我们访问每个网格最多一次。

  • 空间复杂度：O(m \times n)，递归的深度最大可能是整个网格的大小，因此最大可能使用 O(m \times n) 的栈空间。

方法二：深度优先搜索 + 栈

算法

我们可以用栈来实现深度优先搜索算法。这种方法本质与方法一相同，唯一的区别是：

  • 方法一通过函数的调用来表示接下来想要遍历哪些土地，让下一层函数来访问这些土地。而方法二把接下来想要遍历的土地放在栈里，然后在取出这些土地的时候访问它们。

  • 访问每一片土地时，我们将对围绕它四个方向进行探索，找到还未访问的土地，加入到栈 stack 中；

  • 另外，只要栈 stack 不为空，就说明我们还有土地待访问，那么就从栈中取出一个元素并访问。

[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        ans = 0
        for i, l in enumerate(grid):
            for j, n in enumerate(l):
                cur = 0
                stack = [(i, j)]
                while stack:
                    cur_i, cur_j = stack.pop()
                    if cur_i < 0 or cur_j < 0 or cur_i == len(grid) or cur_j == len(grid[0]) or grid[cur_i][cur_j] != 1:
                        continue
                    cur += 1
                    grid[cur_i][cur_j] = 0
                    for di, dj in [[0, 1], [0, -1], [1, 0], [-1, 0]]:
                        next_i, next_j = cur_i + di, cur_j + dj
                        stack.append((next_i, next_j))
                ans = max(ans, cur)
        return ans
[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int ans = 0;
        for (int i = 0; i != grid.size(); ++i) {
            for (int j = 0; j != grid[0].size(); ++j) {
                int cur = 0;
                stack<int> stacki;
                stack<int> stackj;
                stacki.push(i);
                stackj.push(j);
                while (!stacki.empty()) {
                    int cur_i = stacki.top(), cur_j = stackj.top();
                    stacki.pop();
                    stackj.pop();
                    if (cur_i < 0 || cur_j < 0 || cur_i == grid.size() || cur_j == grid[0].size() || grid[cur_i][cur_j] != 1) {
                        continue;
                    }
                    ++cur;
                    grid[cur_i][cur_j] = 0;
                    int di[4] = {0, 0, 1, -1};
                    int dj[4] = {1, -1, 0, 0};
                    for (int index = 0; index != 4; ++index) {
                        int next_i = cur_i + di[index], next_j = cur_j + dj[index];
                        stacki.push(next_i);
                        stackj.push(next_j);
                    }
                }
                ans = max(ans, cur);
            }
        }
        return ans;
    }
};
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        int ans = 0;
        for (int i = 0; i != grid.length; ++i) {
            for (int j = 0; j != grid[0].length; ++j) {
                int cur = 0;
                Deque<Integer> stacki = new LinkedList<Integer>();
                Deque<Integer> stackj = new LinkedList<Integer>();
                stacki.push(i);
                stackj.push(j);
                while (!stacki.isEmpty()) {
                    int cur_i = stacki.pop(), cur_j = stackj.pop();
                    if (cur_i < 0 || cur_j < 0 || cur_i == grid.length || cur_j == grid[0].length || grid[cur_i][cur_j] != 1) {
                        continue;
                    }
                    ++cur;
                    grid[cur_i][cur_j] = 0;
                    int[] di = {0, 0, 1, -1};
                    int[] dj = {1, -1, 0, 0};
                    for (int index = 0; index != 4; ++index) {
                        int next_i = cur_i + di[index], next_j = cur_j + dj[index];
                        stacki.push(next_i);
                        stackj.push(next_j);
                    }
                }
                ans = Math.max(ans, cur);
            }
        }
        return ans;
    }
}

复杂度分析

  • 时间复杂度：O(m \times n)。其中 m 是给定网格中的行数，n 是列数。我们访问每个网格最多一次。

  • 空间复杂度：O(m \times n)，栈中最多会存放所有的土地，土地的数量最多为 m \times n 块，因此使用的空间为 O(m \times n)。

方法三：广度优先搜索

算法

我们把方法二中的栈改为队列，每次从队首取出土地，并将接下来想要遍历的土地放在队尾，就实现了广度优先搜索算法。

[sol3-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        ans = 0
        for i, l in enumerate(grid):
            for j, n in enumerate(l):
                cur = 0
                q = collections.deque([(i, j)])
                while q:
                    cur_i, cur_j = q.popleft()
                    if cur_i < 0 or cur_j < 0 or cur_i == len(grid) or cur_j == len(grid[0]) or grid[cur_i][cur_j] != 1:
                        continue
                    cur += 1
                    grid[cur_i][cur_j] = 0
                    for di, dj in [[0, 1], [0, -1], [1, 0], [-1, 0]]:
                        next_i, next_j = cur_i + di, cur_j + dj
                        q.append((next_i, next_j))
                ans = max(ans, cur)
        return ans
[sol3-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int ans = 0;
        for (int i = 0; i != grid.size(); ++i) {
            for (int j = 0; j != grid[0].size(); ++j) {
                int cur = 0;
                queue<int> queuei;
                queue<int> queuej;
                queuei.push(i);
                queuej.push(j);
                while (!queuei.empty()) {
                    int cur_i = queuei.front(), cur_j = queuej.front();
                    queuei.pop();
                    queuej.pop();
                    if (cur_i < 0 || cur_j < 0 || cur_i == grid.size() || cur_j == grid[0].size() || grid[cur_i][cur_j] != 1) {
                        continue;
                    }
                    ++cur;
                    grid[cur_i][cur_j] = 0;
                    int di[4] = {0, 0, 1, -1};
                    int dj[4] = {1, -1, 0, 0};
                    for (int index = 0; index != 4; ++index) {
                        int next_i = cur_i + di[index], next_j = cur_j + dj[index];
                        queuei.push(next_i);
                        queuej.push(next_j);
                    }
                }
                ans = max(ans, cur);
            }
        }
        return ans;
    }
};
[sol3-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        int ans = 0;
        for (int i = 0; i != grid.length; ++i) {
            for (int j = 0; j != grid[0].length; ++j) {
                int cur = 0;
                Queue<Integer> queuei = new LinkedList<Integer>();
                Queue<Integer> queuej = new LinkedList<Integer>();
                queuei.offer(i);
                queuej.offer(j);
                while (!queuei.isEmpty()) {
                    int cur_i = queuei.poll(), cur_j = queuej.poll();
                    if (cur_i < 0 || cur_j < 0 || cur_i == grid.length || cur_j == grid[0].length || grid[cur_i][cur_j] != 1) {
                        continue;
                    }
                    ++cur;
                    grid[cur_i][cur_j] = 0;
                    int[] di = {0, 0, 1, -1};
                    int[] dj = {1, -1, 0, 0};
                    for (int index = 0; index != 4; ++index) {
                        int next_i = cur_i + di[index], next_j = cur_j + dj[index];
                        queuei.offer(next_i);
                        queuej.offer(next_j);
                    }
                }
                ans = Math.max(ans, cur);
            }
        }
        return ans;
    }
}

复杂度分析

  • 时间复杂度：O(m \times n)。其中 m 是给定网格中的行数，n 是列数。我们访问每个网格最多一次。

  • 空间复杂度：O(m \times n)，队列中最多会存放所有的土地，土地的数量最多为 m \times n 块，因此使用的空间为 O(m \times n)。

 Comments
On this page
LCR 105-岛屿的最大面积