LCR 107-01 矩阵

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：

**输入：** mat = **** [[0,0,0],[0,1,0],[0,0,0]]
**输出：** [[0,0,0],[0,1,0],[0,0,0]]

示例 2：

**输入：** mat = **** [[0,0,0],[0,1,0],[1,1,1]]
**输出：** [[0,0,0],[0,1,0],[1,2,1]]

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• mat 中至少有一个 0

注意：本题与主站 542 题相同：https://leetcode-cn.com/problems/01-matrix/

方法一：广度优先搜索

思路

对于矩阵中的每一个元素，如果它的值为 0，那么离它最近的 0 就是它自己。如果它的值为 1，那么我们就需要找出离它最近的 0，并且返回这个距离值。那么我们如何对于矩阵中的每一个 1，都快速地找到离它最近的 0 呢？

我们不妨从一个简化版本的问题开始考虑起。假设这个矩阵中恰好只有一个 0，我们应该怎么做？由于矩阵中只有一个 0，那么对于每一个 1，离它最近的 0 就是那个唯一的 0。如何求出这个距离呢？我们可以想到两种做法：

• 如果 0 在矩阵中的位置是 (i_0, j_0)，1 在矩阵中的位置是 (i_1, j_1)，那么我们可以直接算出 0 和 1 之间的距离。因为我们从 1 到 0 需要在水平方向走 |i_0 - i_1| 步，竖直方向走 |j_0 - j_1| 步，那么它们之间的距离就为 |i_0 - i_1| + |j_0 - j_1|；

• 我们可以从 0 的位置开始进行 广度优先搜索。广度优先搜索可以找到从起点到其余所有点的 最短距离，因此如果我们从 0 开始搜索，每次搜索到一个 1，就可以得到 0 到这个 1 的最短距离，也就离这个 1 最近的 0 的距离了（因为矩阵中只有一个 0）。

  举个例子，如果我们的矩阵为：

  _ _ _ _
  _ 0 _ _
  _ _ _ _
  _ _ _ _

  其中只有一个 0，剩余的 1 我们用短横线表示。如果我们从 0 开始进行广度优先搜索，那么结果依次为：

  _ _ _ _         _ 1 _ _         2 1 2 _         2 1 2 3         2 1 2 3
  _ 0 _ _   ==>   1 0 1 _   ==>   1 0 1 2   ==>   1 0 1 2   ==>   1 0 1 2
  _ _ _ _         _ 1 _ _         2 1 2 _         2 1 2 3         2 1 2 3
  _ _ _ _         _ _ _ _         _ 2 _ _         3 2 3 _         3 2 3 4

  也就是说，在广度优先搜索的每一步中，如果我们从矩阵中的位置 x 搜索到了位置 y，并且 y 还没有被搜索过，那么位置 y 离 0 的距离就等于位置 x 离 0 的距离加上 1。

对于上面的两种做法，第一种看上去简洁有效，只需要对每一个位置计算就行；第二种需要实现广度优先搜索，会复杂一些。但是，别忘了我们的题目中会有不止一个 0，这样以来，如果我们要使用第一种做法，就必须对于每个 1 计算一次它到所有的 0 的距离，再从中取一个最小值，时间复杂度会非常高，无法通过本地。而对于第二种做法，我们可以很有效地处理有多个 0 的情况。

事实上，第一种做法也是可以处理多个 0 的情况的，但没有那么直观。感兴趣的读者可以在理解完方法一（即本方法）之后阅读方法二，那里介绍了第一种做法是如何扩展的。

处理的方法很简单：我们在进行广度优先搜索的时候会使用到队列，在只有一个 0 的时候，我们在搜索前会把这个 0 的位置加入队列，才能开始进行搜索；如果有多个 0，我们只需要把这些 0 的位置都加入队列就行了。

我们还是举一个例子，在这个例子中，有两个 0：

_ _ _ _
_ 0 _ _
_ _ 0 _
_ _ _ _

我们会把这两个 0 的位置都加入初始队列中，随后我们进行广度优先搜索，找到所有距离为 1 的 1：

_ 1 _ _
1 0 1 _
_ 1 0 1
_ _ 1 _

接着重复步骤，直到搜索完成：

_ 1 _ _         2 1 2 _         2 1 2 3
1 0 1 _   ==>   1 0 1 2   ==>   1 0 1 2
_ 1 0 1         2 1 0 1         2 1 0 1
_ _ 1 _         _ 2 1 2         3 2 1 2

这样做为什么是正确的呢？

• 我们需要对于每一个 1 找到离它最近的 0。如果只有一个 0 的话，我们从这个 0 开始广度优先搜索就可以完成任务了；

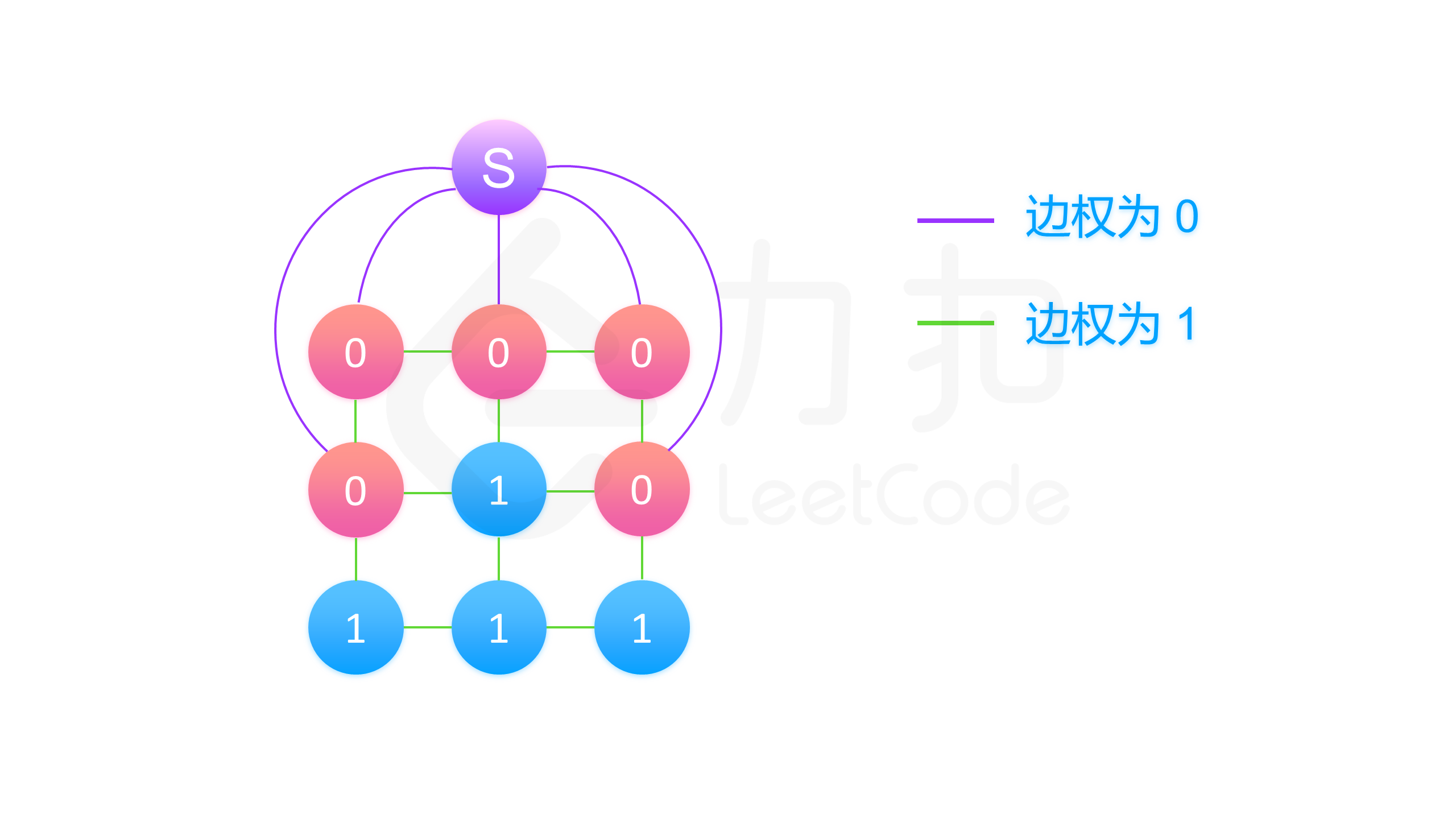
• 但在实际的题目中，我们会有不止一个 0。我们会想，要是我们可以把这些 0 看成一个整体好了。有了这样的想法，我们可以添加一个「超级零」，它与矩阵中所有的 0 相连，这样的话，任意一个 1 到它最近的 0 的距离，会等于这个 1 到「超级零」的距离减去一。由于我们只有一个「超级零」，我们就以它为起点进行广度优先搜索。这个「超级零」只和矩阵中的 0 相连，所以在广度优先搜索的第一步中，「超级零」会被弹出队列，而所有的 0 会被加入队列，它们到「超级零」的距离为 1。这就等价于：一开始我们就将所有的 0 加入队列，它们的初始距离为 0。这样以来，在广度优先搜索的过程中，我们每遇到一个 1，就得到了它到「超级零」的距离减去一，也就是 这个 1 到最近的 0 的距离。

下图中就展示了我们方法：

熟悉「最短路」的读者应该知道，我们所说的「超级零」实际上就是一个「超级源点」。在最短路问题中，如果我们要求多个源点出发的最短路时，一般我们都会建立一个「超级源点」连向所有的源点，用「超级源点」到终点的最短路等价多个源点到终点的最短路。

[sol1-C++]

class Solution {
private:
    static constexpr int dirs[4][2] = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };

public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        vector<vector<int>> dist(m, vector<int>(n));
        vector<vector<int>> seen(m, vector<int>(n));
        queue<pair<int, int>> q;
        // 将所有的 0 添加进初始队列中
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == 0) {
                    q.emplace(i, j);
                    seen[i][j] = 1;
                }
            }
        }

        // 广度优先搜索
        while (!q.empty()) {
            auto [i, j] = q.front();
            q.pop();
            for (int d = 0; d < 4; ++d) {
                int ni = i + dirs[d][0];
                int nj = j + dirs[d][1];
                if (ni >= 0 && ni < m && nj >= 0 && nj < n && !seen[ni][nj]) {
                    dist[ni][nj] = dist[i][j] + 1;
                    q.emplace(ni, nj);
                    seen[ni][nj] = 1;
                }
            }
        }

        return dist;
    }
};

[sol1-Java]

class Solution {
    static int[][] dirs = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };

    public int[][] updateMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        int[][] dist = new int[m][n];
        boolean[][] seen = new boolean[m][n];
        Queue<int[]> queue = new LinkedList<int[]>();
        // 将所有的 0 添加进初始队列中
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == 0) {
                    queue.offer(new int[]{i, j});
                    seen[i][j] = true;
                }
            }
        }

        // 广度优先搜索
        while (!queue.isEmpty()) {
            int[] cell = queue.poll();
            int i = cell[0], j = cell[1];
            for (int d = 0; d < 4; ++d) {
                int ni = i + dirs[d][0];
                int nj = j + dirs[d][1];
                if (ni >= 0 && ni < m && nj >= 0 && nj < n && !seen[ni][nj]) {
                    dist[ni][nj] = dist[i][j] + 1;
                    queue.offer(new int[]{ni, nj});
                    seen[ni][nj] = true;
                }
            }
        }

        return dist;
    }
}

[sol1-Python3]

class Solution:
    def updateMatrix(self, matrix: List[List[int]]) -> List[List[int]]:
        m, n = len(matrix), len(matrix[0])
        dist = [[0] * n for _ in range(m)]
        zeroes_pos = [(i, j) for i in range(m) for j in range(n) if matrix[i][j] == 0]
        # 将所有的 0 添加进初始队列中
        q = collections.deque(zeroes_pos)
        seen = set(zeroes_pos)

        # 广度优先搜索
        while q:
            i, j = q.popleft()
            for ni, nj in [(i - 1, j), (i + 1, j), (i, j - 1), (i, j + 1)]:
                if 0 <= ni < m and 0 <= nj < n and (ni, nj) not in seen:
                    dist[ni][nj] = dist[i][j] + 1
                    q.append((ni, nj))
                    seen.add((ni, nj))
        
        return dist

复杂度分析

• 时间复杂度：O(mn)，其中 m 为矩阵行数，n 为矩阵列数，即矩阵元素个数。广度优先搜索中每个位置最多只会被加入队列一次，因此只需要 O(mn) 的时间复杂度。

• 空间复杂度：O(mn)，其中 m 为矩阵行数，n 为矩阵列数，即矩阵元素个数。除答案数组外，最坏情况下矩阵里所有元素都为 0，全部被加入队列中，此时需要 O(mn) 的空间复杂度。

方法二：动态规划

我们回想方法一中的「遗珠」：

如果 0 在矩阵中的位置是 (i_0, j_0)，1 在矩阵中的位置是 (i_1, j_1)，那么我们可以直接算出 0 和 1 之间的距离。因为我们从 1 到 0 需要在水平方向走 |i_0 - i_1| 步，竖直方向走 |j_0 - j_1| 步，那么它们之间的距离就为 |i_0 - i_1| + |j_0 - j_1|。

对于矩阵中的任意一个 1 以及一个 0，我们如何从这个 1 到达 0 并且距离最短呢？根据上面的做法，我们可以从 1 开始，先在水平方向移动，直到与 0 在同一列，随后再在竖直方向上移动，直到到达 0 的位置。这样一来，从一个固定的 1 走到任意一个 0，在距离最短的前提下可能有四种方法：

• 只有 水平向左移动 和 竖直向上移动；

• 只有 水平向左移动 和 竖直向下移动；

• 只有 水平向右移动 和 竖直向上移动；

• 只有 水平向右移动 和 竖直向下移动。

例如下面这一个矩阵包含四个 0。从中心位置的 1 移动到这四个 0，就需要使用四种不同的方法：

0 _ _ _ 0
_ _ _ _ _
_ _ 1 _ _
_ _ _ _ _
0 _ _ _ 0

这样以来，我们就可以使用动态规划解决这个问题了。我们用 f(i, j) 表示位置 (i, j) 到最近的 0 的距离。如果我们只能「水平向左移动」和「竖直向上移动」，那么我们可以向上移动一步，再移动 f(i - 1, j) 步到达某一个 0，也可以向左移动一步，再移动 f(i, j - 1) 步到达某一个 0。因此我们可以写出如下的状态转移方程：

f(i, j) =
\begin{cases}
1 + \min\big(f(i - 1, j), f(i, j - 1)\big) &, \text{位置 } (i, j) \text{ 的元素为 } 1 \
0 &, \text{位置 } (i, j) \text{ 的元素为 } 0
\end{cases}

对于另外三种移动方法，我们也可以写出类似的状态转移方程，得到四个 f(i, j) 的值，那么其中最小的值就表示位置 (i, j) 到最近的 0 的距离。

[sol2-C++]

class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        // 初始化动态规划的数组，所有的距离值都设置为一个很大的数
        vector<vector<int>> dist(m, vector<int>(n, INT_MAX / 2));
        // 如果 (i, j) 的元素为 0，那么距离为 0
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == 0) {
                    dist[i][j] = 0;
                }
            }
        }
        // 只有 水平向左移动 和 竖直向上移动，注意动态规划的计算顺序
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i - 1 >= 0) {
                    dist[i][j] = min(dist[i][j], dist[i - 1][j] + 1);
                }
                if (j - 1 >= 0) {
                    dist[i][j] = min(dist[i][j], dist[i][j - 1] + 1);
                }
            }
        }
        // 只有 水平向左移动 和 竖直向下移动，注意动态规划的计算顺序
        for (int i = m - 1; i >= 0; --i) {
            for (int j = 0; j < n; ++j) {
                if (i + 1 < m) {
                    dist[i][j] = min(dist[i][j], dist[i + 1][j] + 1);
                }
                if (j - 1 >= 0) {
                    dist[i][j] = min(dist[i][j], dist[i][j - 1] + 1);
                }
            }
        }
        // 只有 水平向右移动 和 竖直向上移动，注意动态规划的计算顺序
        for (int i = 0; i < m; ++i) {
            for (int j = n - 1; j >= 0; --j) {
                if (i - 1 >= 0) {
                    dist[i][j] = min(dist[i][j], dist[i - 1][j] + 1);
                }
                if (j + 1 < n) {
                    dist[i][j] = min(dist[i][j], dist[i][j + 1] + 1);
                }
            }
        }
        // 只有 水平向右移动 和 竖直向下移动，注意动态规划的计算顺序
        for (int i = m - 1; i >= 0; --i) {
            for (int j = n - 1; j >= 0; --j) {
                if (i + 1 < m) {
                    dist[i][j] = min(dist[i][j], dist[i + 1][j] + 1);
                }
                if (j + 1 < n) {
                    dist[i][j] = min(dist[i][j], dist[i][j + 1] + 1);
                }
            }
        }
        return dist;
    }
};

[sol2-Java]

class Solution {
    static int[][] dirs = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };

    public int[][] updateMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        // 初始化动态规划的数组，所有的距离值都设置为一个很大的数
        int[][] dist = new int[m][n];
        for (int i = 0; i < m; ++i) {
            Arrays.fill(dist[i], Integer.MAX_VALUE / 2);
        }
        // 如果 (i, j) 的元素为 0，那么距离为 0
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == 0) {
                    dist[i][j] = 0;
                }
            }
        }
        // 只有 水平向左移动 和 竖直向上移动，注意动态规划的计算顺序
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i - 1 >= 0) {
                    dist[i][j] = Math.min(dist[i][j], dist[i - 1][j] + 1);
                }
                if (j - 1 >= 0) {
                    dist[i][j] = Math.min(dist[i][j], dist[i][j - 1] + 1);
                }
            }
        }
        // 只有 水平向左移动 和 竖直向下移动，注意动态规划的计算顺序
        for (int i = m - 1; i >= 0; --i) {
            for (int j = 0; j < n; ++j) {
                if (i + 1 < m) {
                    dist[i][j] = Math.min(dist[i][j], dist[i + 1][j] + 1);
                }
                if (j - 1 >= 0) {
                    dist[i][j] = Math.min(dist[i][j], dist[i][j - 1] + 1);
                }
            }
        }
        // 只有 水平向右移动 和 竖直向上移动，注意动态规划的计算顺序
        for (int i = 0; i < m; ++i) {
            for (int j = n - 1; j >= 0; --j) {
                if (i - 1 >= 0) {
                    dist[i][j] = Math.min(dist[i][j], dist[i - 1][j] + 1);
                }
                if (j + 1 < n) {
                    dist[i][j] = Math.min(dist[i][j], dist[i][j + 1] + 1);
                }
            }
        }
        // 只有 水平向右移动 和 竖直向下移动，注意动态规划的计算顺序
        for (int i = m - 1; i >= 0; --i) {
            for (int j = n - 1; j >= 0; --j) {
                if (i + 1 < m) {
                    dist[i][j] = Math.min(dist[i][j], dist[i + 1][j] + 1);
                }
                if (j + 1 < n) {
                    dist[i][j] = Math.min(dist[i][j], dist[i][j + 1] + 1);
                }
            }
        }
        return dist;
    }
}

[sol2-Python3]

class Solution:
    def updateMatrix(self, matrix: List[List[int]]) -> List[List[int]]:
        m, n = len(matrix), len(matrix[0])
        # 初始化动态规划的数组，所有的距离值都设置为一个很大的数
        dist = [[10**9] * n for _ in range(m)]
        # 如果 (i, j) 的元素为 0，那么距离为 0
        for i in range(m):
            for j in range(n):
                if matrix[i][j] == 0:
                    dist[i][j] = 0
        # 只有 水平向左移动 和 竖直向上移动，注意动态规划的计算顺序
        for i in range(m):
            for j in range(n):
                if i - 1 >= 0:
                    dist[i][j] = min(dist[i][j], dist[i - 1][j] + 1)
                if j - 1 >= 0:
                    dist[i][j] = min(dist[i][j], dist[i][j - 1] + 1)
        # 只有 水平向左移动 和 竖直向下移动，注意动态规划的计算顺序
        for i in range(m - 1, -1, -1):
            for j in range(n):
                if i + 1 < m:
                    dist[i][j] = min(dist[i][j], dist[i + 1][j] + 1)
                if j - 1 >= 0:
                    dist[i][j] = min(dist[i][j], dist[i][j - 1] + 1)
        # 只有 水平向右移动 和 竖直向上移动，注意动态规划的计算顺序
        for i in range(m):
            for j in range(n - 1, -1, -1):
                if i - 1 >= 0:
                    dist[i][j] = min(dist[i][j], dist[i - 1][j] + 1)
                if j + 1 < n:
                    dist[i][j] = min(dist[i][j], dist[i][j + 1] + 1)
        # 只有 水平向右移动 和 竖直向下移动，注意动态规划的计算顺序
        for i in range(m - 1, -1, -1):
            for j in range(n - 1, -1, -1):
                if i + 1 < m:
                    dist[i][j] = min(dist[i][j], dist[i + 1][j] + 1)
                if j + 1 < n:
                    dist[i][j] = min(dist[i][j], dist[i][j + 1] + 1)
        return dist

复杂度分析

• 时间复杂度：O(mn)，其中 m 为矩阵行数，n 为矩阵列数。计算 dist 数组的过程中我们需要遍历四次矩阵，因此时间复杂度为 O(4mn)=O(mn)。

• 空间复杂度：O(1)，这里我们只计算额外的空间复杂度。除了答案数组以外，我们只需要常数空间存放若干变量。

方法三：动态规划的常数优化

我们发现方法二中的代码有一些重复计算的地方。实际上，我们只需要保留

• 只有 水平向左移动 和 竖直向上移动；

• 只有 水平向右移动 和 竖直向下移动。

这两者即可。这里不会给出详细的证明，有兴趣的读者可以自己思考。

[sol3-C++]

class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        // 初始化动态规划的数组，所有的距离值都设置为一个很大的数
        vector<vector<int>> dist(m, vector<int>(n, INT_MAX / 2));
        // 如果 (i, j) 的元素为 0，那么距离为 0
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == 0) {
                    dist[i][j] = 0;
                }
            }
        }
        // 只有 水平向左移动 和 竖直向上移动，注意动态规划的计算顺序
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i - 1 >= 0) {
                    dist[i][j] = min(dist[i][j], dist[i - 1][j] + 1);
                }
                if (j - 1 >= 0) {
                    dist[i][j] = min(dist[i][j], dist[i][j - 1] + 1);
                }
            }
        }
        // 只有 水平向右移动 和 竖直向下移动，注意动态规划的计算顺序
        for (int i = m - 1; i >= 0; --i) {
            for (int j = n - 1; j >= 0; --j) {
                if (i + 1 < m) {
                    dist[i][j] = min(dist[i][j], dist[i + 1][j] + 1);
                }
                if (j + 1 < n) {
                    dist[i][j] = min(dist[i][j], dist[i][j + 1] + 1);
                }
            }
        }
        return dist;
    }
};

[sol3-Java]

class Solution {
    static int[][] dirs = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };

    public int[][] updateMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        // 初始化动态规划的数组，所有的距离值都设置为一个很大的数
        int[][] dist = new int[m][n];
        for (int i = 0; i < m; ++i) {
            Arrays.fill(dist[i], Integer.MAX_VALUE / 2);
        }
        // 如果 (i, j) 的元素为 0，那么距离为 0
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == 0) {
                    dist[i][j] = 0;
                }
            }
        }
        // 只有 水平向左移动 和 竖直向上移动，注意动态规划的计算顺序
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i - 1 >= 0) {
                    dist[i][j] = Math.min(dist[i][j], dist[i - 1][j] + 1);
                }
                if (j - 1 >= 0) {
                    dist[i][j] = Math.min(dist[i][j], dist[i][j - 1] + 1);
                }
            }
        }
        // 只有 水平向右移动 和 竖直向下移动，注意动态规划的计算顺序
        for (int i = m - 1; i >= 0; --i) {
            for (int j = n - 1; j >= 0; --j) {
                if (i + 1 < m) {
                    dist[i][j] = Math.min(dist[i][j], dist[i + 1][j] + 1);
                }
                if (j + 1 < n) {
                    dist[i][j] = Math.min(dist[i][j], dist[i][j + 1] + 1);
                }
            }
        }
        return dist;
    }
}

[sol3-Python3]

class Solution:
    def updateMatrix(self, matrix: List[List[int]]) -> List[List[int]]:
        m, n = len(matrix), len(matrix[0])
        # 初始化动态规划的数组，所有的距离值都设置为一个很大的数
        dist = [[10**9] * n for _ in range(m)]
        # 如果 (i, j) 的元素为 0，那么距离为 0
        for i in range(m):
            for j in range(n):
                if matrix[i][j] == 0:
                    dist[i][j] = 0
        # 只有 水平向左移动 和 竖直向上移动，注意动态规划的计算顺序
        for i in range(m):
            for j in range(n):
                if i - 1 >= 0:
                    dist[i][j] = min(dist[i][j], dist[i - 1][j] + 1)
                if j - 1 >= 0:
                    dist[i][j] = min(dist[i][j], dist[i][j - 1] + 1)
        # 只有 水平向右移动 和 竖直向下移动，注意动态规划的计算顺序
        for i in range(m - 1, -1, -1):
            for j in range(n - 1, -1, -1):
                if i + 1 < m:
                    dist[i][j] = min(dist[i][j], dist[i + 1][j] + 1)
                if j + 1 < n:
                    dist[i][j] = min(dist[i][j], dist[i][j + 1] + 1)
        return dist

复杂度分析

• 时间复杂度：O(mn)，其中 m 为矩阵行数，n 为矩阵列数。计算 dist 数组的过程中我们需要遍历两次矩阵，因此时间复杂度为 O(2mn)=O(mn)。

• 空间复杂度：O(1)，这里我们只计算额外的空间复杂度。除了答案数组以外，我们只需要常数空间存放若干变量。