现有一种使用英语字母的外星文语言,这门语言的字母顺序与英语顺序不同。
给定一个字符串列表 words ,作为这门语言的词典,words 中的字符串已经 按这门新语言的字母顺序进行了排序 。
请你根据该词典还原出此语言中已知的字母顺序,并 按字母递增顺序 排列。若不存在合法字母顺序,返回 "" 。若存在多种可能的合法字母顺序,返回其中任意一种 顺序即可。
字符串 s 字典顺序小于 字符串 t 有两种情况:
在第一个不同字母处,如果 s 中的字母在这门外星语言的字母顺序中位于 t 中字母之前,那么 s 的字典顺序小于 t 。
如果前面 min(s.length, t.length) 字母都相同,那么 s.length < t.length 时,s 的字典顺序也小于 t 。
示例 1:
**输入:** words = ["wrt","wrf","er","ett","rftt"]
**输出:** "wertf"
示例 2:
**输入:** words = ["z","x"]
**输出:** "zx"
示例 3:
**输入:** words = ["z","x","z"]
**输出:** ""
**解释:** 不存在合法字母顺序,因此返回 "" 。
提示:
1 <= words.length <= 1001 <= words[i].length <= 100words[i] 仅由小写英文字母组成
注意:本题与主站 269 题相同: https://leetcode-cn.com/problems/alien-dictionary/
前言 这道题是拓扑排序问题。外星文字典中的字母和字母顺序可以看成有向图,字典顺序即为所有字母的一种排列,满足每一条有向边的起点字母和终点字母的顺序都和这两个字母在排列中的顺序相同,该排列即为有向图的拓扑排序。
只有当有向图中无环时,才有拓扑排序,且拓扑排序可能不止一种。如果有向图中有环,则环内的字母不存在符合要求的排列,因此没有拓扑排序。
使用拓扑排序求解时,将外星文字典中的每个字母看成一个节点,将字母之间的顺序关系看成有向边。对于外星文字典中的两个相邻单词,同时从左到右遍历,当遇到第一个不相同的字母时,该位置的两个字母之间即存在顺序关系。
以下两种情况不存在合法字母顺序:
字母之间的顺序关系存在由至少 2 个字母组成的环,例如 words} = [\text{a"}, \text{b”}, \text{``a”}];
相邻两个单词满足后面的单词是前面的单词的前缀,且后面的单词的长度小于前面的单词的长度,例如 words} = [\text{ab"}, \text{a”}]。
其余情况下都存在合法字母顺序,可以使用拓扑排序得到字典顺序。
拓扑排序可以使用深度优先搜索或广度优先搜索实现,以下分别介绍两种实现方法。
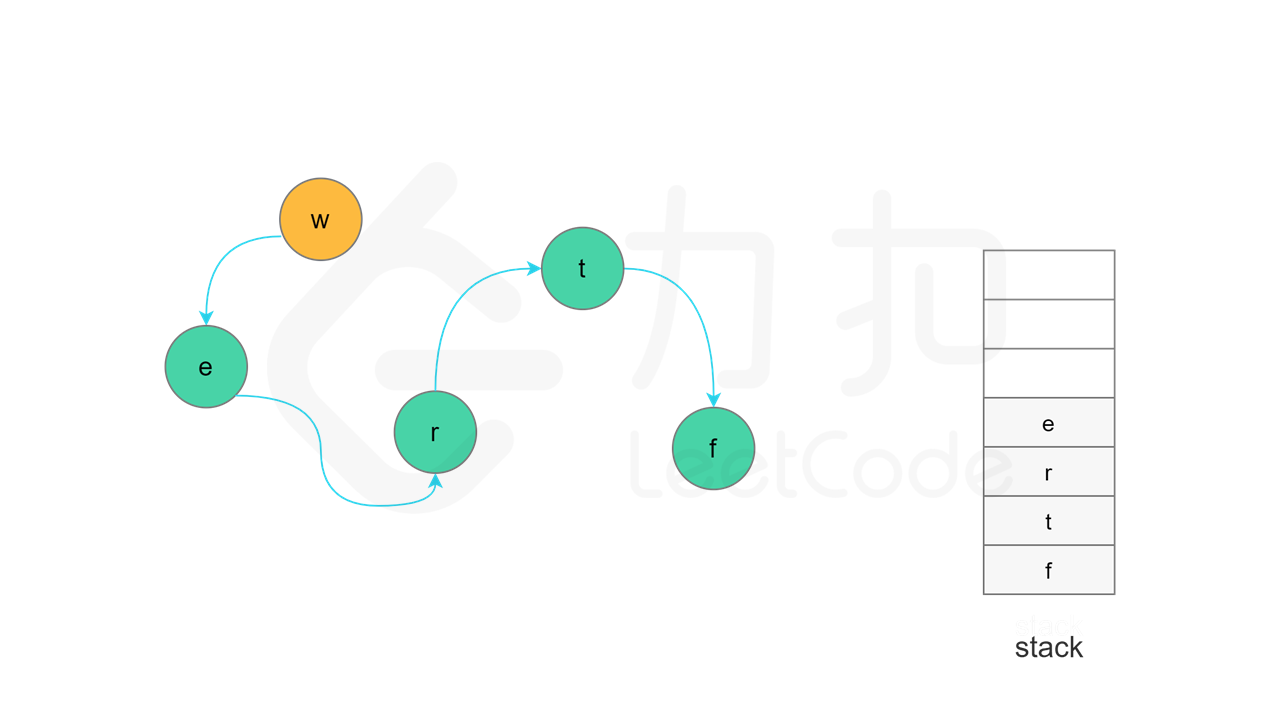
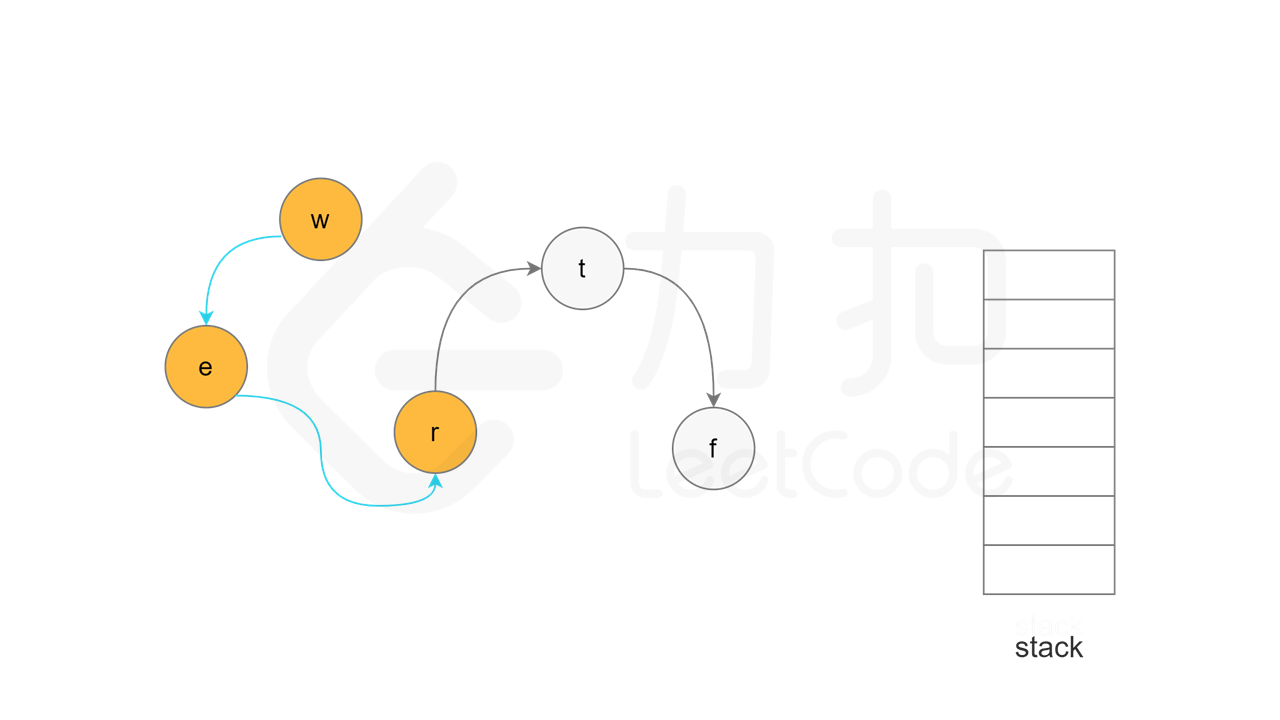
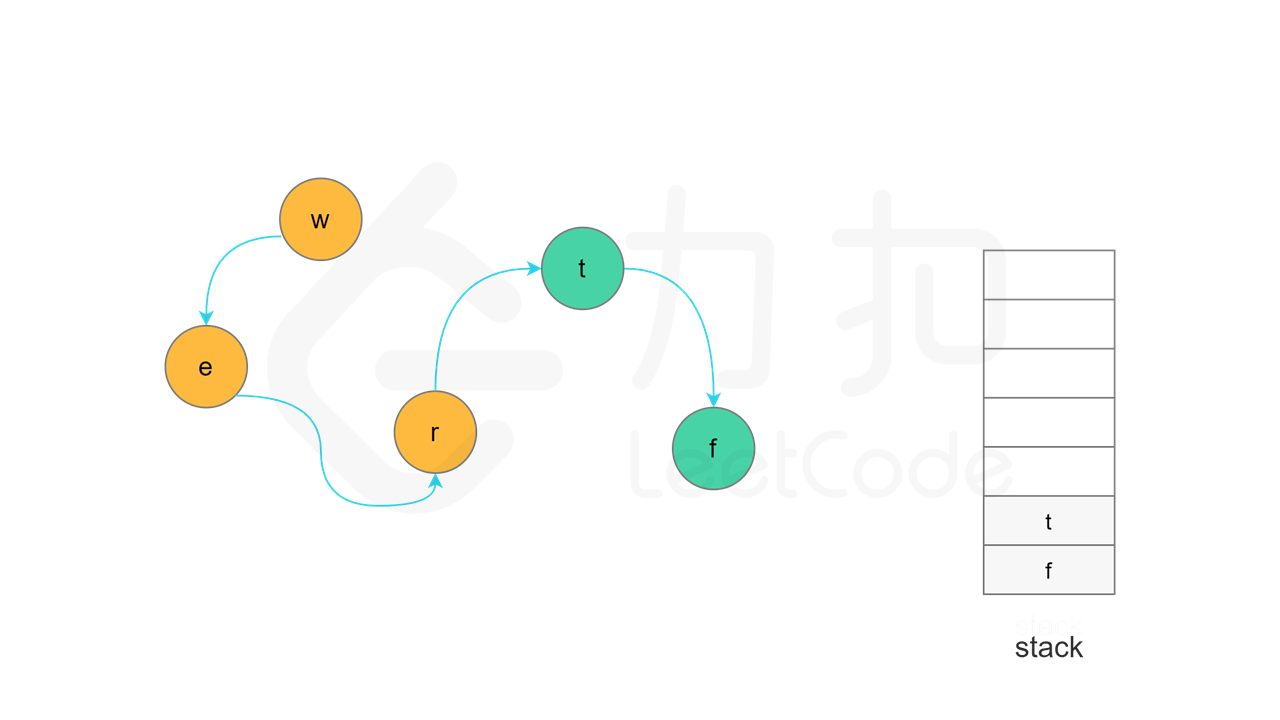
方法一:拓扑排序 + 深度优先搜索 使用深度优先搜索实现拓扑排序的总体思想是:对于一个特定节点,如果该节点的所有相邻节点都已经搜索完成,则该节点也会变成已经搜索完成的节点,在拓扑排序中,该节点位于其所有相邻节点的前面。一个节点的相邻节点指的是从该节点出发通过一条有向边可以到达的节点。
由于拓扑排序的顺序和搜索完成的顺序相反,因此需要使用一个栈存储所有已经搜索完成的节点。深度优先搜索的过程中需要维护每个节点的状态,每个节点的状态可能有三种情况:「未访问」、「访问中」和「已访问」。初始时,所有节点的状态都是「未访问」。
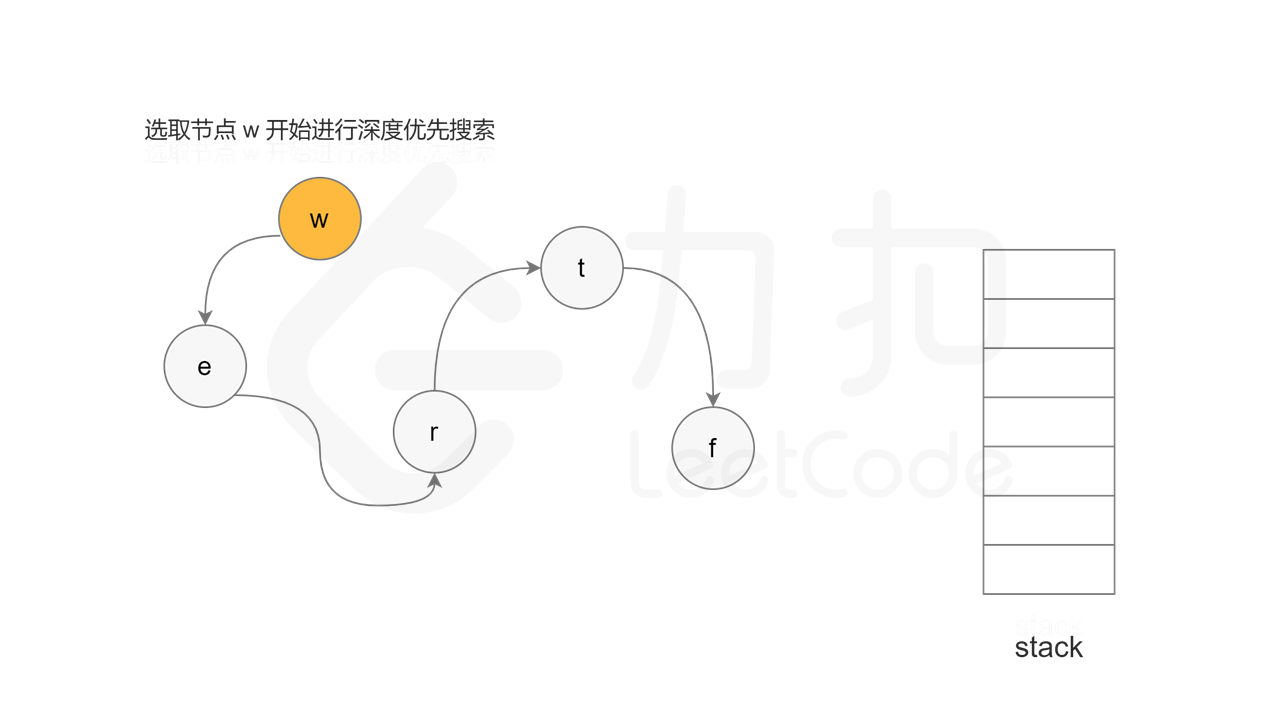
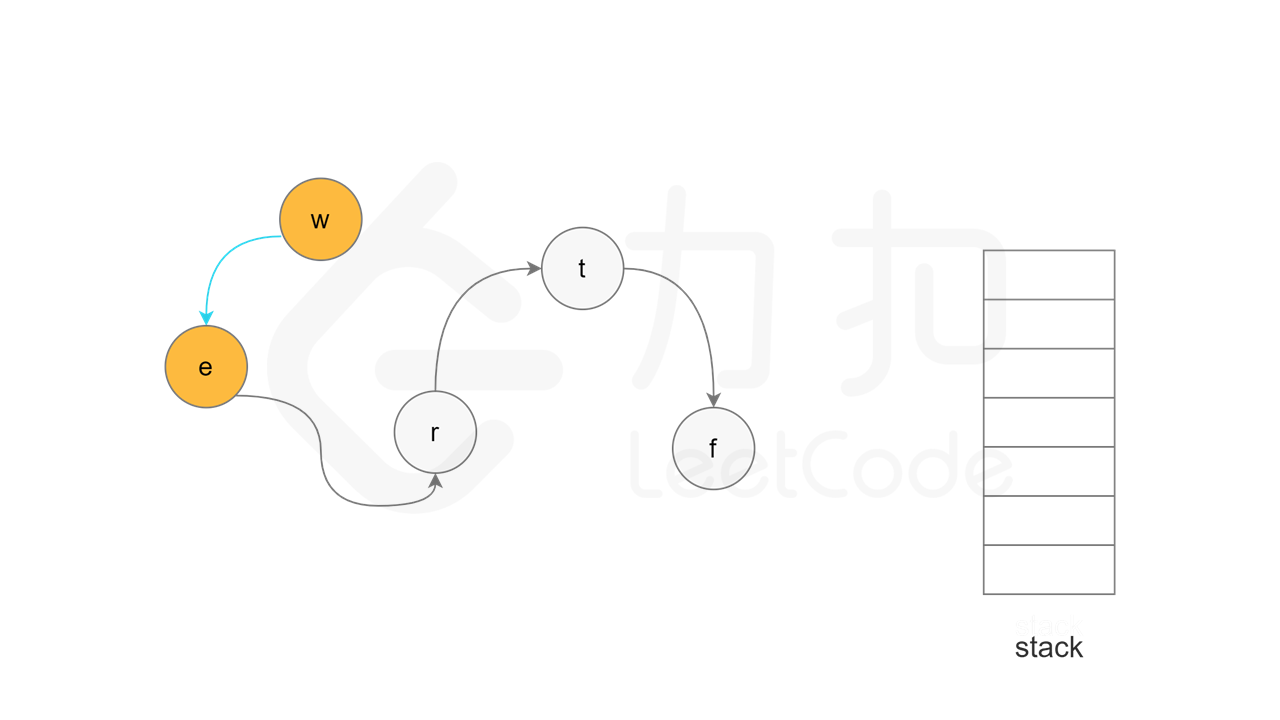
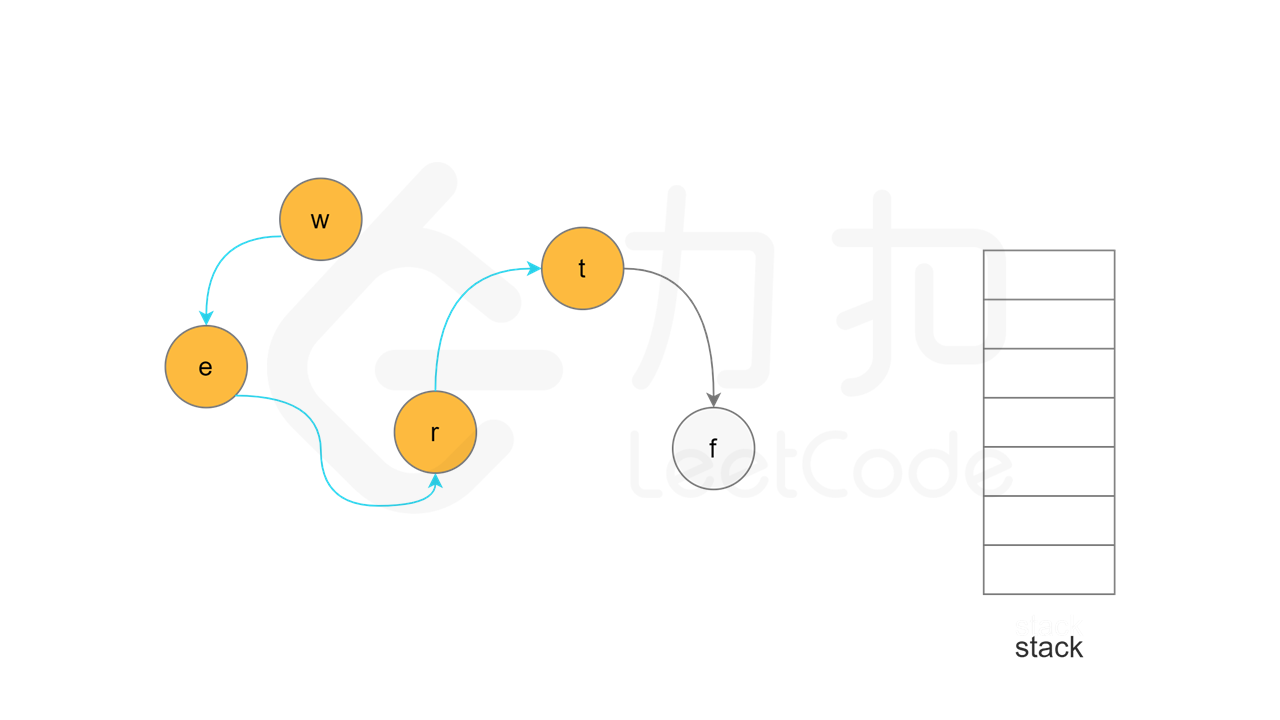
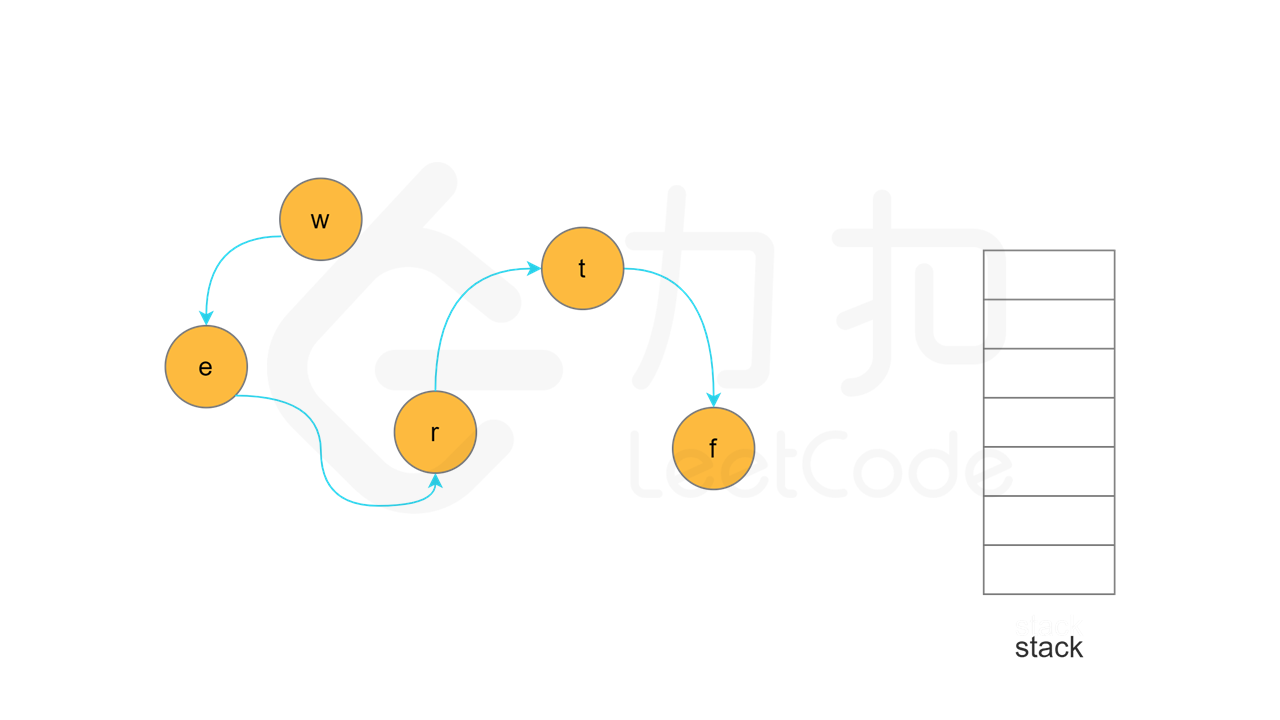
每一轮搜索时,任意选取一个「未访问」的节点 u,从节点 u 开始深度优先搜索。将节点 u 的状态更新为「访问中」,对于每个与节点 u 相邻的节点 v,判断节点 v 的状态,执行如下操作:
如果节点 v 的状态是「未访问」,则继续搜索节点 v;
如果节点 v 的状态是「访问中」,则找到有向图中的环,因此不存在拓扑排序;
如果节点 v 的状态是「已访问」,则节点 v 已经搜索完成并入栈,节点 u 尚未入栈,因此节点 u 的拓扑顺序一定在节点 v 的前面,不需要执行任何操作。
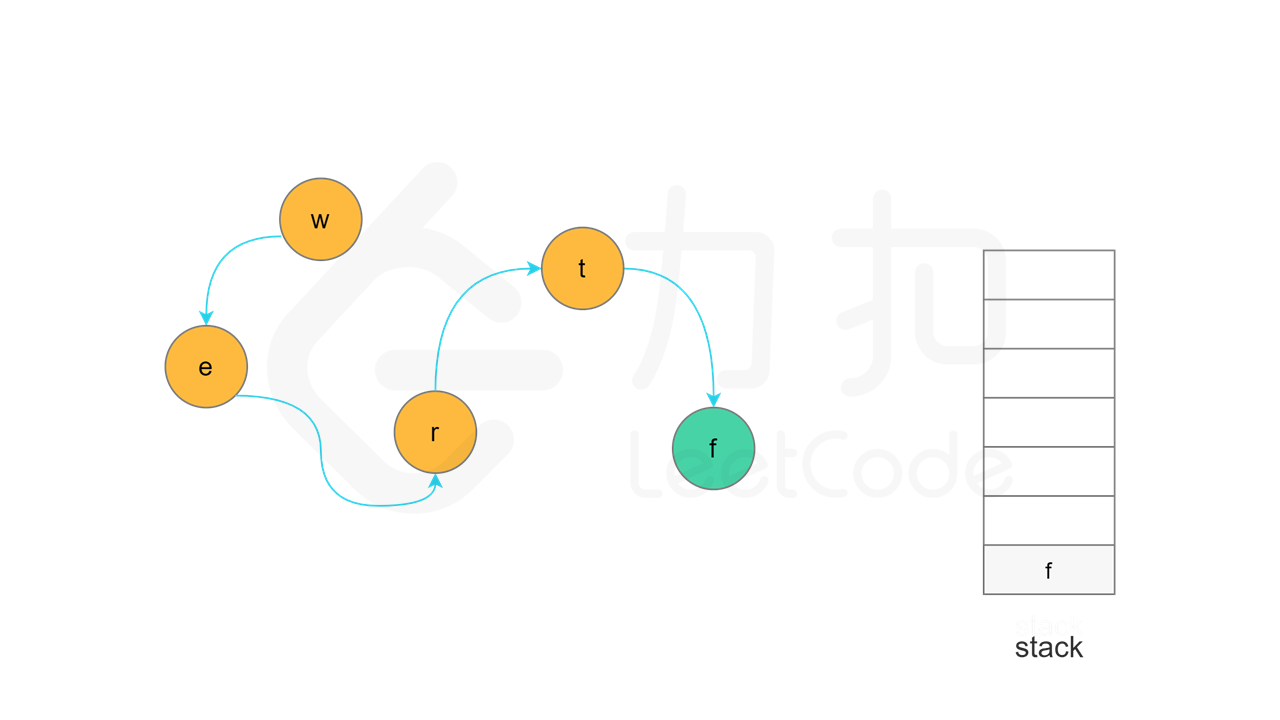
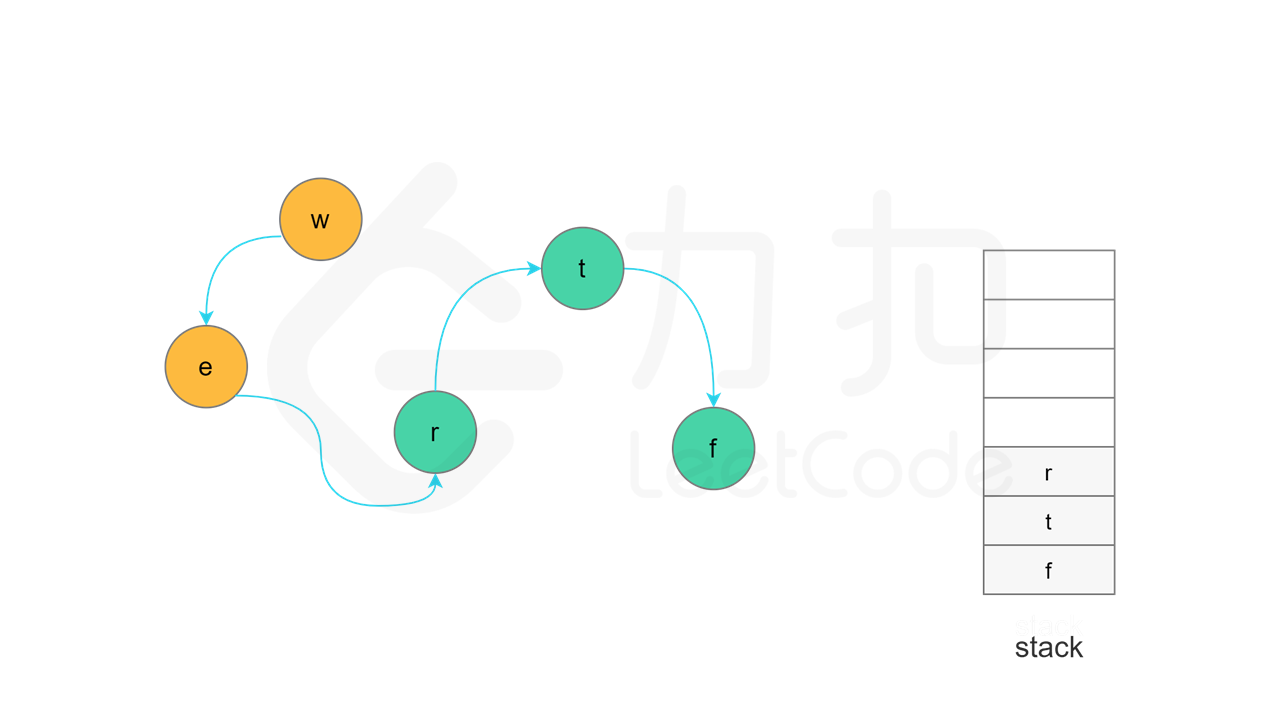
当节点 u 的所有相邻节点的状态都是「已访问」时,将节点 u 的状态更新为「已访问」,并将节点 u 入栈。
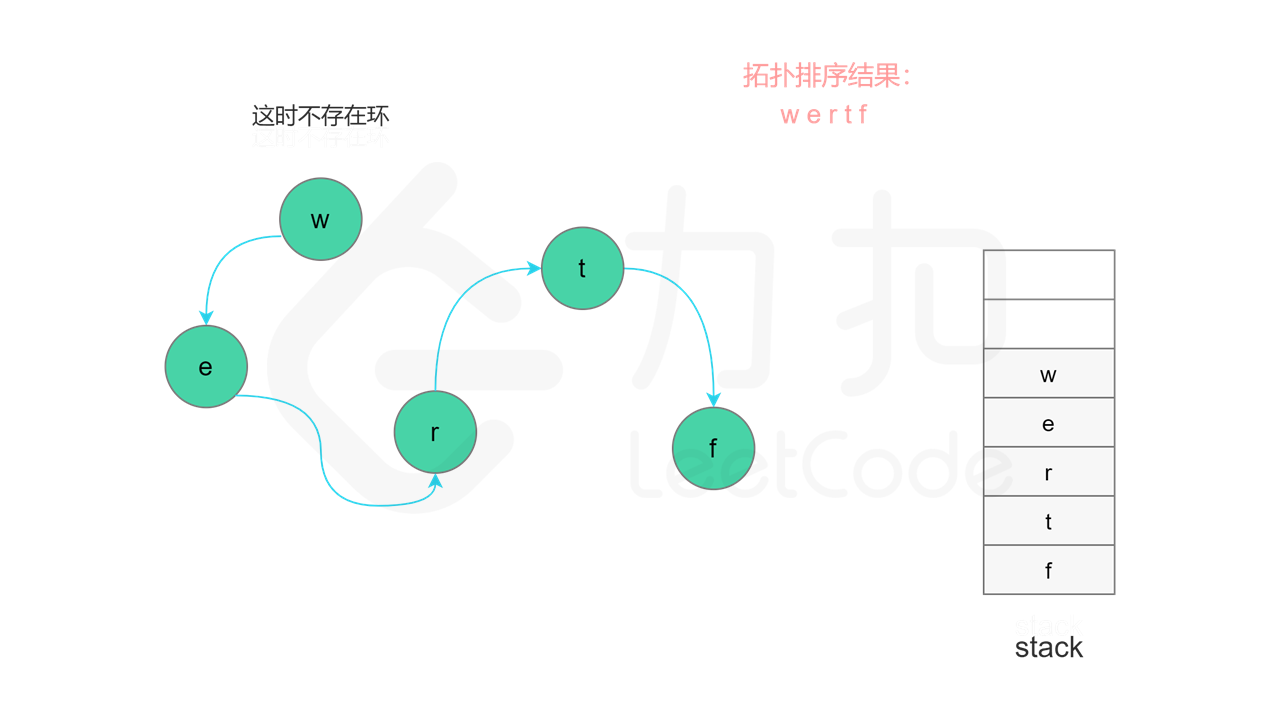
当所有节点都访问结束之后,如果没有找到有向图中的环,则存在拓扑排序,所有节点从栈顶到栈底的顺序即为拓扑排序。
实现方面,由于每个节点是一个字母,因此可以使用字符数组代替栈,当节点入栈时,在字符数组中按照从后往前的顺序依次填入每个字母。当所有节点都访问结束之后,将字符数组转成字符串,即为字典顺序。
<
[sol1-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution : def alienOrder (self, words: List [str ] ) -> str : g = {} for c in words[0 ]: g[c] = [] for s, t in pairwise(words): for c in t: g.setdefault(c, []) for u, v in zip (s, t): if u != v: g[u].append(v) break else : if len (s) > len (t): return "" VISITING, VISITED = 1 , 2 states = {} order = [] def dfs (u: str ) -> bool : states[u] = VISITING for v in g[u]: if v not in states: if not dfs(v): return False elif states[v] == VISITING: return False order.append(u) states[u] = VISITED return True return '' .join(reversed (order)) if all (dfs(u) for u in g if u not in states) else ""
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 class Solution { static final int VISITING = 1 , VISITED = 2 ; Map<Character, List<Character>> edges = new HashMap <Character, List<Character>>(); Map<Character, Integer> states = new HashMap <Character, Integer>(); boolean valid = true ; char [] order; int index; public String alienOrder (String[] words) { int length = words.length; for (String word : words) { int wordLength = word.length(); for (int j = 0 ; j < wordLength; j++) { char c = word.charAt(j); edges.putIfAbsent(c, new ArrayList <Character>()); } } for (int i = 1 ; i < length && valid; i++) { addEdge(words[i - 1 ], words[i]); } order = new char [edges.size()]; index = edges.size() - 1 ; Set<Character> letterSet = edges.keySet(); for (char u : letterSet) { if (!states.containsKey(u)) { dfs(u); } } if (!valid) { return "" ; } return new String (order); } public void addEdge (String before, String after) { int length1 = before.length(), length2 = after.length(); int length = Math.min(length1, length2); int index = 0 ; while (index < length) { char c1 = before.charAt(index), c2 = after.charAt(index); if (c1 != c2) { edges.get(c1).add(c2); break ; } index++; } if (index == length && length1 > length2) { valid = false ; } } public void dfs (char u) { states.put(u, VISITING); List<Character> adjacent = edges.get(u); for (char v : adjacent) { if (!states.containsKey(v)) { dfs(v); if (!valid) { return ; } } else if (states.get(v) == VISITING) { valid = false ; return ; } } states.put(u, VISITED); order[index] = u; index--; } }
[sol1-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 public class Solution { const int VISITING = 1 , VISITED = 2 ; Dictionary<char , IList<char >> edges = new Dictionary<char , IList<char >>(); Dictionary<char , int > states = new Dictionary<char , int >(); bool valid = true ; char [] order; int index; public string AlienOrder (string [] words int length = words.Length; foreach (string word in words) { foreach (char c in word) { if (!edges.ContainsKey(c)) { edges.Add(c, new List<char >()); } } } for (int i = 1 ; i < length && valid; i++) { AddEdge(words[i - 1 ], words[i]); } order = new char [edges.Count]; index = edges.Count - 1 ; Dictionary<char , IList<char >>.KeyCollection letterSet = edges.Keys; foreach (char u in letterSet) { if (!states.ContainsKey(u)) { DFS(u); } } if (!valid) { return "" ; } return new string (order); } public void AddEdge (string before, string after int length1 = before.Length, length2 = after.Length; int length = Math.Min(length1, length2); int index = 0 ; while (index < length) { char c1 = before[index], c2 = after[index]; if (c1 != c2) { edges[c1].Add(c2); break ; } index++; } if (index == length && length1 > length2) { valid = false ; } } public void DFS (char u states.Add(u, VISITING); IList<char > adjacent = edges[u]; foreach (char v in adjacent) { if (!states.ContainsKey(v)) { DFS(v); if (!valid) { return ; } } else if (states[v] == VISITING) { valid = false ; return ; } } states[u] = VISITED; order[index] = u; index--; } }
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 class Solution {public : const int VISITING = 1 , VISITED = 2 ; unordered_map<char , vector<char >> edges; unordered_map<char , int > states; bool valid = true ; string order; int index; string alienOrder (vector<string>& words) { int length = words.size (); for (string & word : words) { int wordLength = word.size (); for (int j = 0 ; j < wordLength; j++) { char c = word[j]; if (!edges.count (c)) { edges[c] = vector <char >(); } } } for (int i = 1 ; i < length && valid; i++) { addEdge (words[i - 1 ], words[i]); } order = string (edges.size (), ' ' ); index = edges.size () - 1 ; for (auto [u, _] : edges) { if (!states.count (u)) { dfs (u); } } if (!valid) { return "" ; } return order; } void addEdge (string before, string after) int length1 = before.size (), length2 = after.size (); int length = min (length1, length2); int index = 0 ; while (index < length) { char c1 = before[index], c2 = after[index]; if (c1 != c2) { edges[c1].emplace_back (c2); break ; } index++; } if (index == length && length1 > length2) { valid = false ; } } void dfs (char u) states[u] = VISITING; for (char v : edges[u]) { if (!states.count (v)) { dfs (v); if (!valid) { return ; } } else if (states[v] == VISITING) { valid = false ; return ; } } states[u] = VISITED; order[index] = u; index--; } };
[sol1-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 #define MIN(a, b) ((a) < (b) ? (a) : (b)) #define VISITING 1 #define VISITED 2 void addEdge (const char *before, const char *after, int **edges, bool *valid) { int length1 = strlen (before), length2 = strlen (after); int length = MIN(length1, length2); int index = 0 ; while (index < length) { char c1 = before[index], c2 = after[index]; if (c1 != c2) { edges[c1 - 'a' ][c2 - 'a' ] = 1 ; break ; } index++; } if (index == length && length1 > length2) { *valid = false ; } } void dfs (int u, char *order, int *index, int **edges, int *states, bool *valid) { states[u] = VISITING; if (edges[u]) { for (int i = 0 ; i < 26 ; i++) { if (edges[u][i]) { if (!states[i]) { dfs(i, order, index, edges, states, valid); if (!valid) { return ; } } else if (states[i] == VISITING) { *valid = false ; return ; } } } } states[u] = VISITED; order[*index] = 'a' + u; (*index)--; } char * alienOrder (char ** words, int wordsSize) { int edgesSize = 0 ; int *edges[26 ]; int states[26 ]; bool valid = true ; for (int i = 0 ; i < 26 ; i++) { edges[i] = NULL ; } memset (states, 0 , sizeof (states)); for (int i = 0 ; i < wordsSize; i++) { int wordLength = strlen (words[i]); for (int j = 0 ; j < wordLength; j++) { char c = words[i][j]; if (!edges[c - 'a' ]) { edges[c - 'a' ] = (int *)malloc (sizeof (int ) * 26 ); memset (edges[c - 'a' ], 0 , sizeof (int ) * 26 ); edgesSize++; } } } for (int i = 1 ; i < wordsSize && valid; i++) { addEdge(words[i - 1 ], words[i], edges, &valid); } char *order = (char *)malloc (sizeof (char ) * (edgesSize + 1 )); memset (order, ' ' , sizeof (char ) * edgesSize); order[edgesSize] = '\0' ; int index = edgesSize - 1 ; for (int i = 0 ; i < 26 ; i++) { if (edges[i] && !states[i]) { dfs(i, order, &index, edges, states, &valid); } } for (int i = 0 ; i < 26 ; i++) { if (edges[i]) { free (edges[i]); } } if (!valid) { order[0 ] = '\0' ; } return order; }
[sol1-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 var alienOrder = function (words ) { const VISITING = 1 , VISITED = 2 ; let valid = true ; const edges = new Map (); const states = new Map (); const length = words.length ; for (const word of words) { const wordLength = word.length ; for (let j = 0 ; j < wordLength; j++) { const c = word[j]; if (!edges.has (c)) { edges.set (c, []); } } } const addEdge = (before, after ) => { const length1 = before.length , length2 = after.length ; const length = Math .min (length1, length2); let index = 0 ; while (index < length) { const c1 = before[index], c2 = after[index]; if (c1 !== c2) { edges.get (c1).push (c2); break ; } index++; } if (index === length && length1 > length2) { valid = false ; } } const dfs = (u ) => { states.set (u, VISITING ); const adjacent = edges.get (u); for (const v of adjacent) { if (!states.has (v)) { dfs (v); if (!valid) { return ; } } else if (states.get (v) === VISITING ) { valid = false ; return ; } } states.set (u, VISITED ); order[index] = u; index--; } for (let i = 1 ; i < length && valid; i++) { addEdge (words[i - 1 ], words[i]); } const order = new Array (edges.size ).fill (0 ); let index = edges.size - 1 ; const letterSet = edges.keys (); for (const u of letterSet) { if (!states.has (u)) { dfs (u); } } if (!valid) { return "" ; } return order.join ('' ); };
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 func alienOrder (words []string ) string { g := map [byte ][]byte {} for _, c := range words[0 ] { g[byte (c)] = nil } next: for i := 1 ; i < len (words); i++ { s, t := words[i-1 ], words[i] for _, c := range t { g[byte (c)] = g[byte (c)] } for j := 0 ; j < len (s) && j < len (t); j++ { if s[j] != t[j] { g[s[j]] = append (g[s[j]], t[j]) continue next } } if len (s) > len (t) { return "" } } const visiting, visited = 1 , 2 order := make ([]byte , len (g)) i := len (g) - 1 state := map [byte ]int {} var dfs func (u byte ) bool dfs = func (u byte ) bool { state[u] = visiting for _, v := range g[u] { if state[v] == 0 { if !dfs(v) { return false } } else if state[v] == visiting { return false } } order[i] = u i-- state[u] = visited return true } for u := range g { if state[u] == 0 && !dfs(u) { return "" } } return string (order) }
复杂度分析
时间复杂度:O(n \times L + |\Sigma|),其中 n 是数组 words 的长度,即字典中的单词数,L 是字典中的平均单词长度,\Sigma 是字典中的字母集合。遍历字典构造有向图需要 O(n \times L) 的时间,由于有向图包含最多 n - 1 条边和 |\Sigma| 个节点,因此深度优先搜索需要 O(n + |\Sigma|) 的时间,总时间复杂度是 O(n \times L + n + |\Sigma|) = O(n \times L + |\Sigma|)。
空间复杂度:O(n + |\Sigma|),其中 n 是数组 words 的长度,即字典中的单词数,\Sigma 是字典中的字母集合。空间复杂度主要取决于存储有向图需要的空间,有向图包含最多 n - 1 条边和 |\Sigma| 个节点。
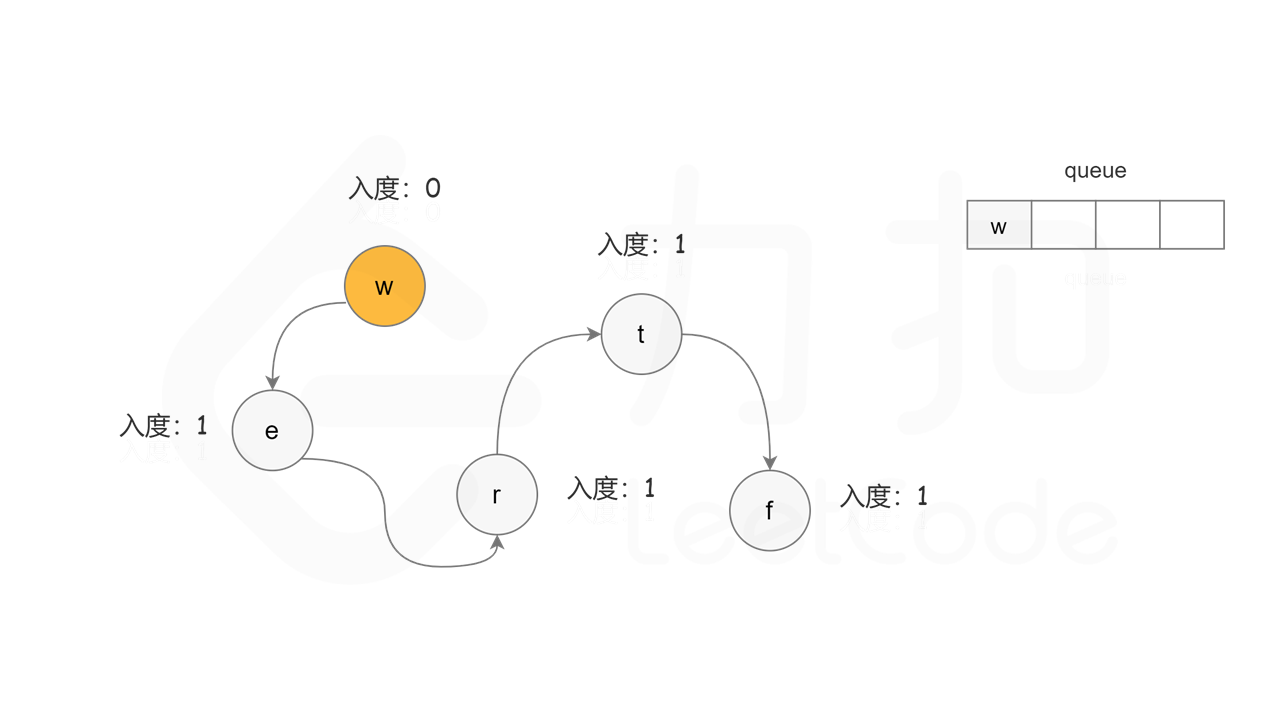
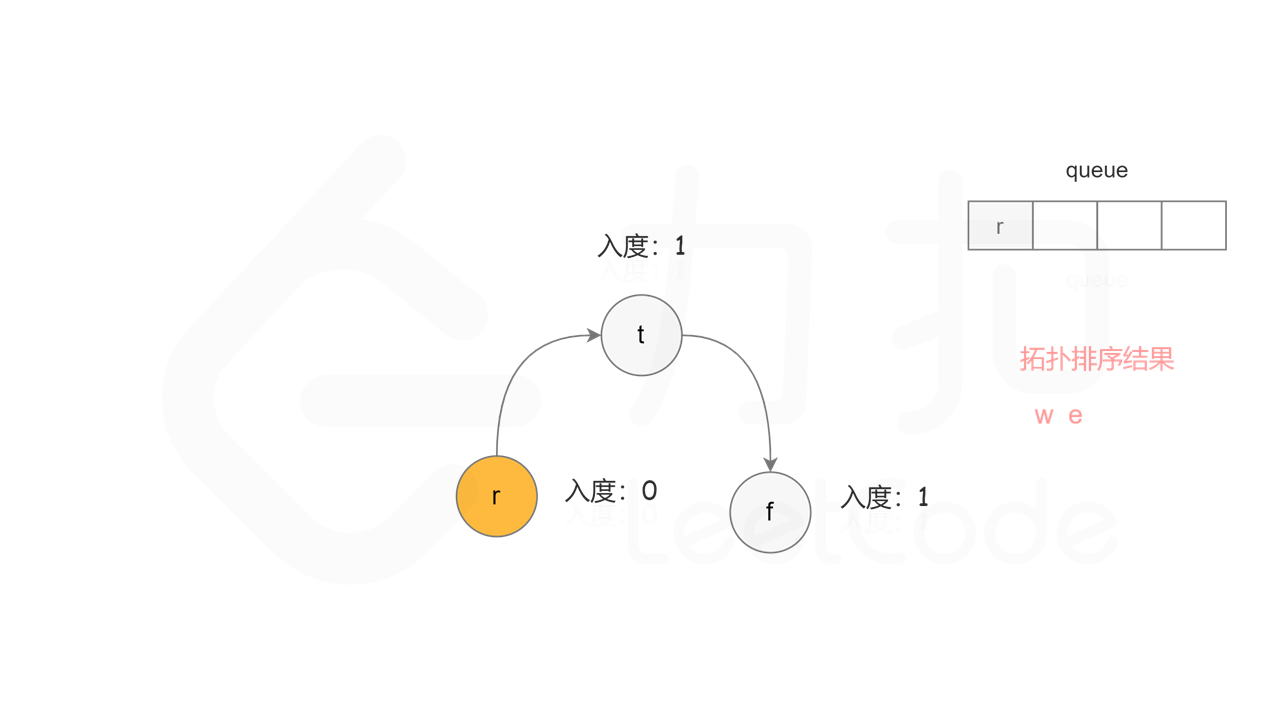
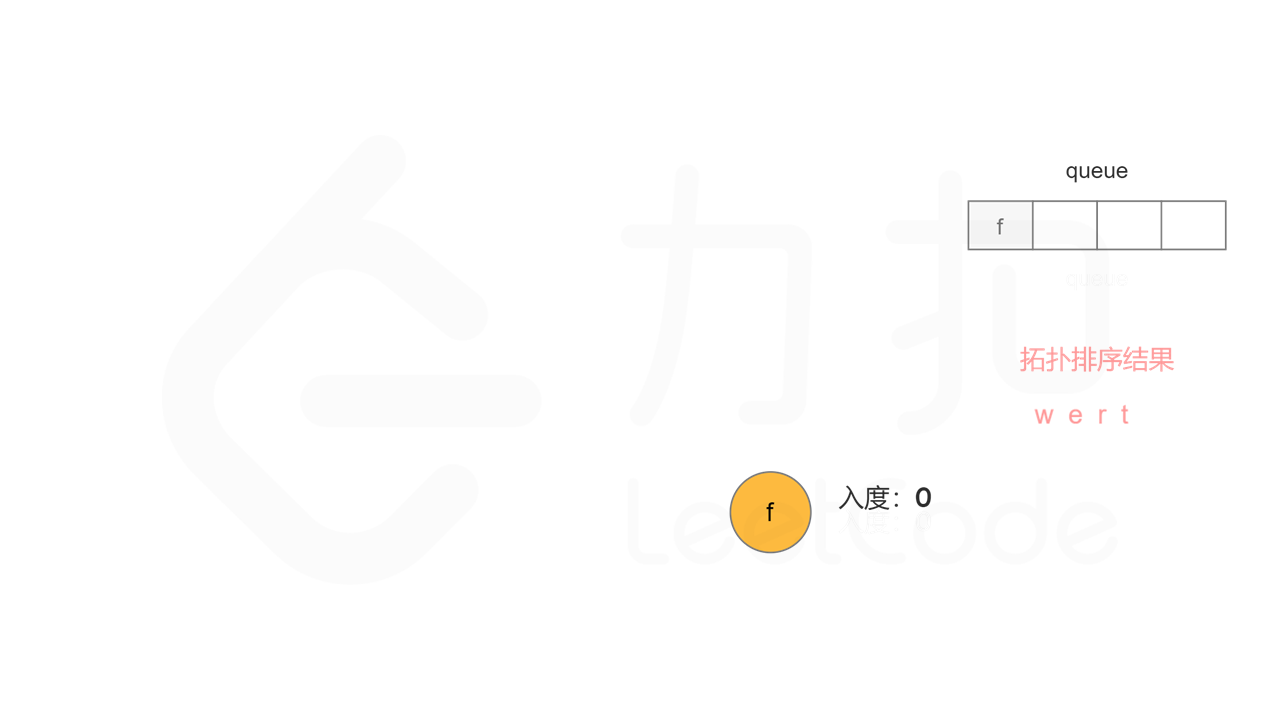
方法二:拓扑排序 + 广度优先搜索 方法一使用深度优先搜索实现拓扑排序,根据每个节点搜索完成的顺序反向得到拓扑排序。使用广度优先搜索实现拓扑排序,则可以正向得到拓扑排序。
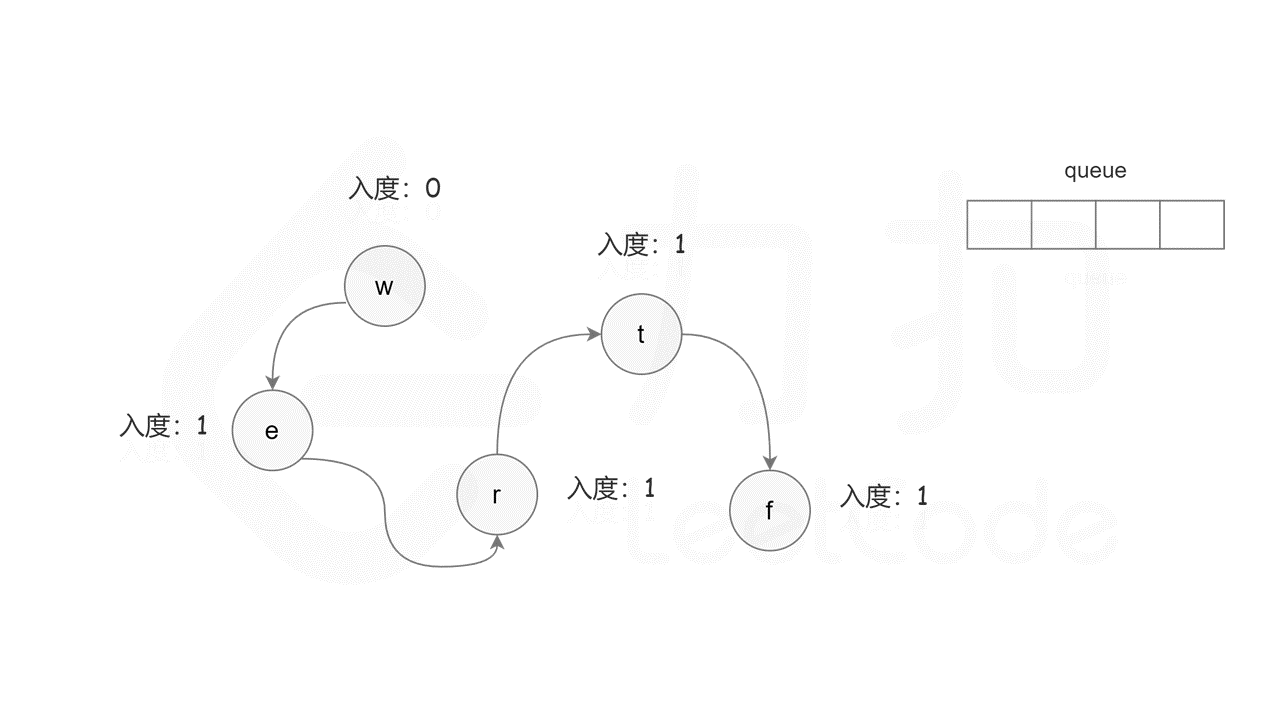
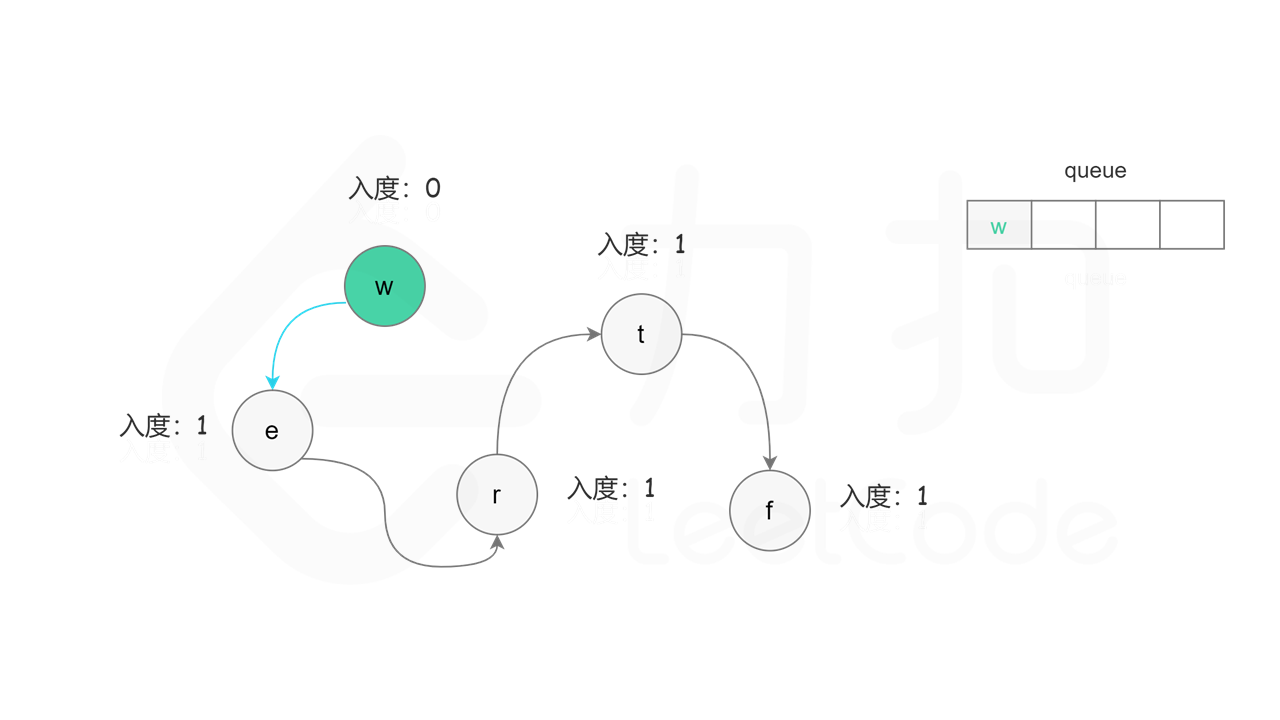
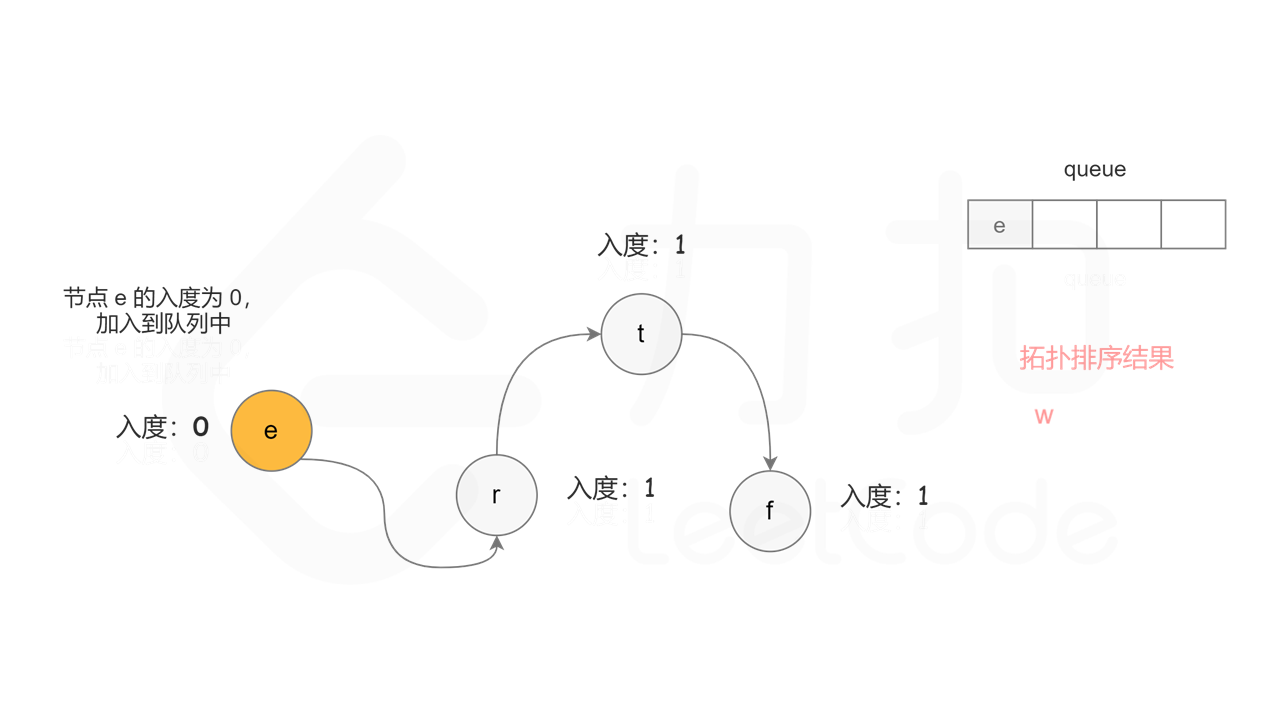
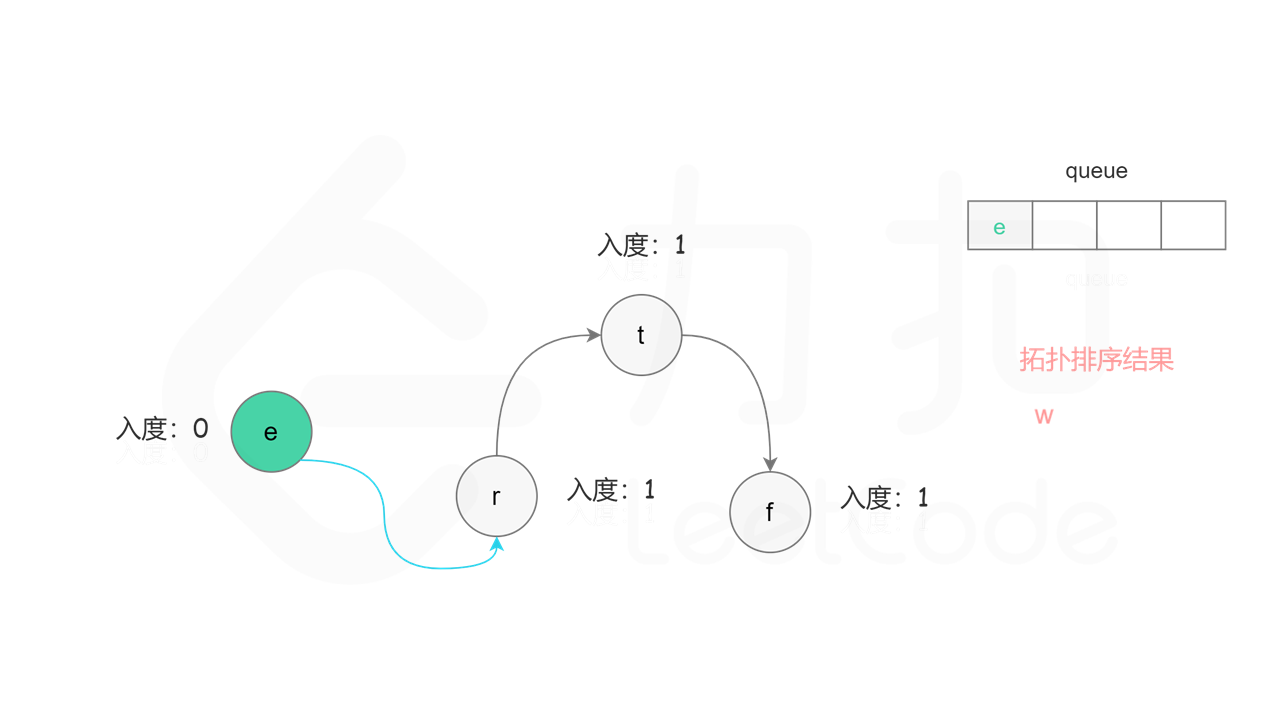
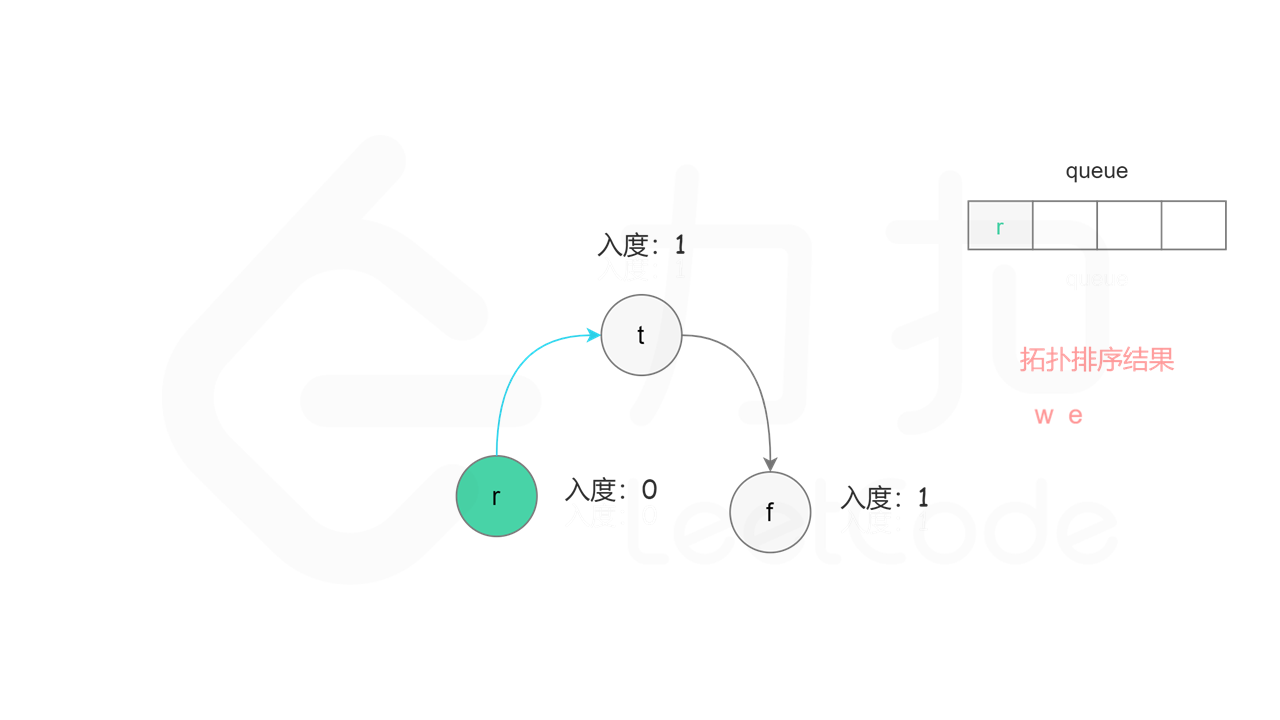
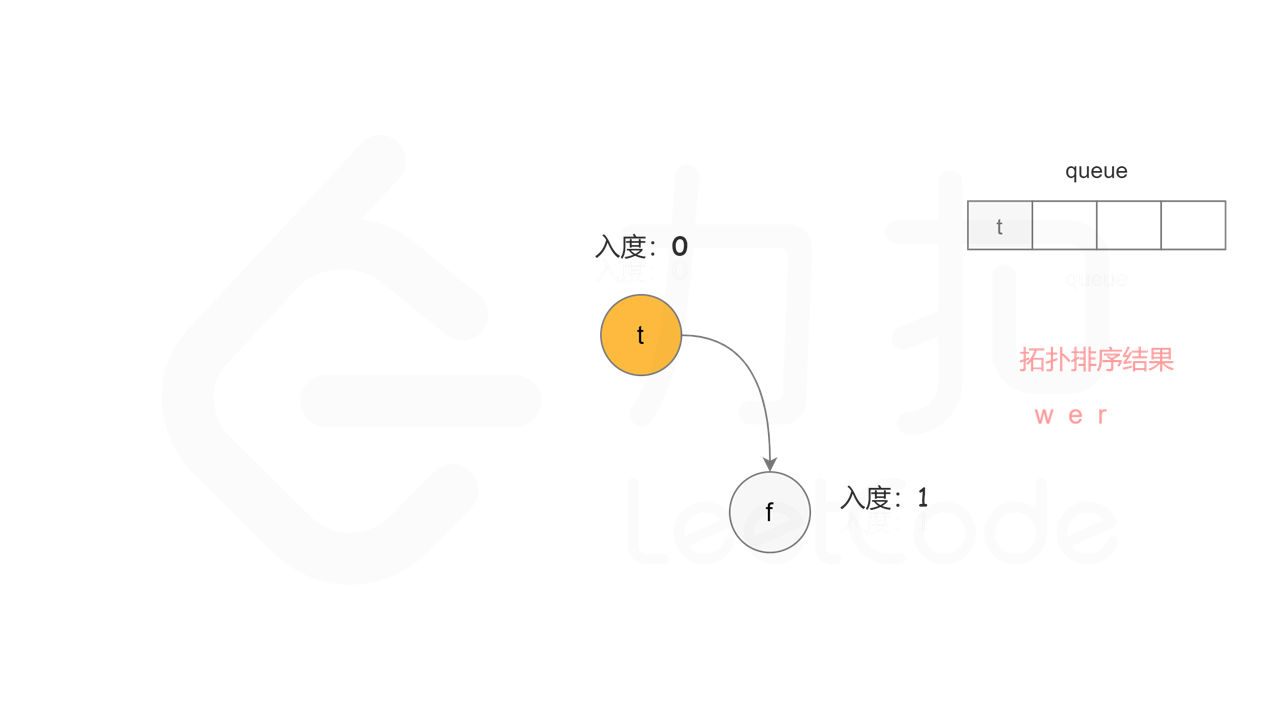
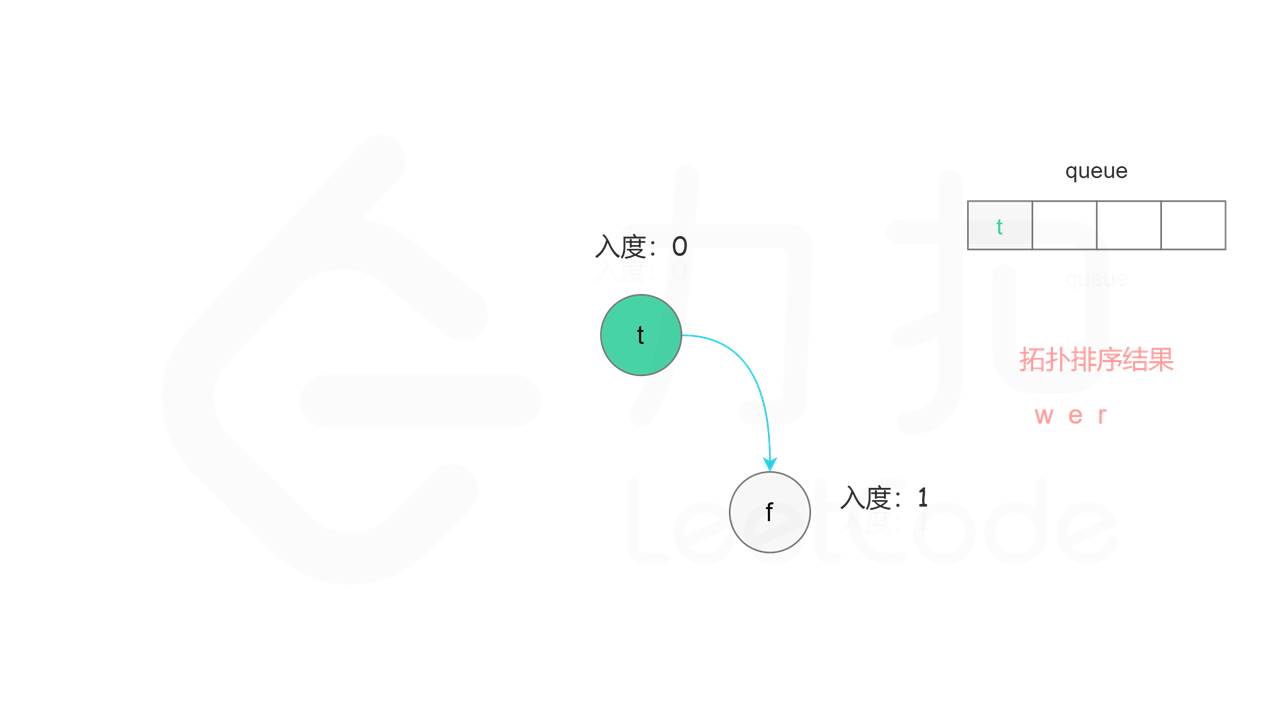
首先计算每个节点的入度,只有入度为 0 的节点可能是拓扑排序中最前面的节点。当一个节点加入拓扑排序之后,该节点的所有相邻节点的入度都减 1,表示相邻节点少了一条入边。当一个节点的入度变成 0,则该节点前面的节点都已经加入拓扑排序,该节点也可以加入拓扑排序。
具体做法是,使用队列存储可以加入拓扑排序的节点,初始时将所有入度为 0 的节点入队列。每次将一个节点出队列并加入拓扑排序中,然后将该节点的所有相邻节点的入度都减 1,如果一个相邻节点的入度变成 0,则将该相邻节点入队列。重复上述操作,直到队列为空时,广度优先搜索结束。
如果有向图中无环,则每个节点都将加入拓扑排序,因此拓扑排序的长度等于字典中的字母个数。如果有向图中有环,则环中的节点不会加入拓扑排序,因此拓扑排序的长度小于字典中的字母个数。广度优先搜索结束时,判断拓扑排序的长度是否等于字典中的字母个数,即可判断有向图中是否有环。
<
[sol2-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution : def alienOrder (self, words: List [str ] ) -> str : g = defaultdict(list ) inDeg = {c: 0 for c in words[0 ]} for s, t in pairwise(words): for c in t: inDeg.setdefault(c, 0 ) for u, v in zip (s, t): if u != v: g[u].append(v) inDeg[v] += 1 break else : if len (s) > len (t): return "" q = [u for u, d in inDeg.items() if d == 0 ] for u in q: for v in g[u]: inDeg[v] -= 1 if inDeg[v] == 0 : q.append(v) return '' .join(q) if len (q) == len (inDeg) else ""
[sol2-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 class Solution { Map<Character, List<Character>> edges = new HashMap <Character, List<Character>>(); Map<Character, Integer> indegrees = new HashMap <Character, Integer>(); boolean valid = true ; public String alienOrder (String[] words) { int length = words.length; for (String word : words) { int wordLength = word.length(); for (int j = 0 ; j < wordLength; j++) { char c = word.charAt(j); edges.putIfAbsent(c, new ArrayList <Character>()); } } for (int i = 1 ; i < length && valid; i++) { addEdge(words[i - 1 ], words[i]); } if (!valid) { return "" ; } Queue<Character> queue = new ArrayDeque <Character>(); Set<Character> letterSet = edges.keySet(); for (char u : letterSet) { if (!indegrees.containsKey(u)) { queue.offer(u); } } StringBuffer order = new StringBuffer (); while (!queue.isEmpty()) { char u = queue.poll(); order.append(u); List<Character> adjacent = edges.get(u); for (char v : adjacent) { indegrees.put(v, indegrees.get(v) - 1 ); if (indegrees.get(v) == 0 ) { queue.offer(v); } } } return order.length() == edges.size() ? order.toString() : "" ; } public void addEdge (String before, String after) { int length1 = before.length(), length2 = after.length(); int length = Math.min(length1, length2); int index = 0 ; while (index < length) { char c1 = before.charAt(index), c2 = after.charAt(index); if (c1 != c2) { edges.get(c1).add(c2); indegrees.put(c2, indegrees.getOrDefault(c2, 0 ) + 1 ); break ; } index++; } if (index == length && length1 > length2) { valid = false ; } } }
[sol2-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 public class Solution { Dictionary<char , IList<char >> edges = new Dictionary<char , IList<char >>(); Dictionary<char , int > indegrees = new Dictionary<char , int >(); bool valid = true ; public string AlienOrder (string [] words int length = words.Length; foreach (string word in words) { foreach (char c in word) { if (!edges.ContainsKey(c)) { edges.Add(c, new List<char >()); } } } for (int i = 1 ; i < length && valid; i++) { AddEdge(words[i - 1 ], words[i]); } if (!valid) { return "" ; } Queue<char > queue = new Queue<char >(); Dictionary<char , IList<char >>.KeyCollection letterSet = edges.Keys; foreach (char u in letterSet) { if (!indegrees.ContainsKey(u)) { queue.Enqueue(u); } } StringBuilder order = new StringBuilder(); while (queue.Count > 0 ) { char u = queue.Dequeue(); order.Append(u); IList<char > adjacent = edges[u]; foreach (char v in adjacent) { indegrees[v]--; if (indegrees[v] == 0 ) { queue.Enqueue(v); } } } return order.Length == edges.Count ? order.ToString() : "" ; } public void AddEdge (string before, string after int length1 = before.Length, length2 = after.Length; int length = Math.Min(length1, length2); int index = 0 ; while (index < length) { char c1 = before[index], c2 = after[index]; if (c1 != c2) { edges[c1].Add(c2); if (!indegrees.ContainsKey(c2)) { indegrees.Add(c2, 0 ); } indegrees[c2]++; break ; } index++; } if (index == length && length1 > length2) { valid = false ; } } }
[sol2-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 class Solution {public : unordered_map<char , vector<char >> edges; unordered_map<char , int > indegrees; bool valid = true ; string alienOrder (vector<string>& words) { int length = words.size (); for (auto word : words) { int wordLength = word.size (); for (int j = 0 ; j < wordLength; j++) { char c = word[j]; if (!edges.count (c)) { edges[c] = vector <char >(); } } } for (int i = 1 ; i < length && valid; i++) { addEdge (words[i - 1 ], words[i]); } if (!valid) { return "" ; } queue<char > qu; for (auto [u, _] : edges) { if (!indegrees.count (u)) { qu.emplace (u); } } string order; while (!qu.empty ()) { char u = qu.front (); qu.pop (); order.push_back (u); for (char v : edges[u]) { indegrees[v]--; if (indegrees[v] == 0 ) { qu.emplace (v); } } } return order.size () == edges.size () ? order : "" ; } void addEdge (string before, string after) int length1 = before.size (), length2 = after.size (); int length = min (length1, length2); int index = 0 ; while (index < length) { char c1 = before[index], c2 = after[index]; if (c1 != c2) { edges[c1].emplace_back (c2); indegrees[c2] += 1 ; break ; } index++; } if (index == length && length1 > length2) { valid = false ; } } };
[sol2-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 #define MIN(a, b) ((a) < (b) ? (a) : (b)) void addEdge (const char *before, const char *after, int **edges, int *indegrees, bool *valid) { int length1 = strlen (before), length2 = strlen (after); int length = MIN(length1, length2); int index = 0 ; while (index < length) { char c1 = before[index], c2 = after[index]; if (c1 != c2 ) { if (edges[c1 - 'a' ][c2 - 'a' ] == 0 ) { edges[c1 - 'a' ][c2 - 'a' ] = 1 ; indegrees[c2 - 'a' ]++; } break ; } index++; } if (index == length && length1 > length2) { *valid = false ; } } char * alienOrder (char ** words, int wordsSize) { int edgesSize = 0 ; int *edges[26 ]; int indegrees[26 ]; bool valid = true ; memset (indegrees, 0 , sizeof (indegrees)); for (int i = 0 ; i < 26 ; i++) { edges[i] = NULL ; } for (int i = 0 ; i < wordsSize; i++) { int wordLength = strlen (words[i]); for (int j = 0 ; j < wordLength; j++) { char c = words[i][j]; if (!edges[c - 'a' ]) { edges[c - 'a' ] = (int *)malloc (sizeof (int ) * 26 ); memset (edges[c - 'a' ], 0 , sizeof (int ) * 26 ); edgesSize++; } } } for (int i = 1 ; i < wordsSize && valid; i++) { addEdge(words[i - 1 ], words[i], edges, indegrees, &valid); } char *order = (char *)malloc (sizeof (char ) * (edgesSize + 1 )); order[edgesSize] = '\0' ; int * queue = (int *)malloc (sizeof (int ) * 26 ); int head = 0 ; int tail = 0 ; int pos = 0 ; for (int i = 0 ; i < 26 ; i++) { if (edges[i] && !indegrees[i]) { queue [tail++] = i; } } while (head != tail) { int u = queue [head++]; order[pos++] = 'a' + u; for (int i = 0 ; i < 26 ; i++) { if (edges[u][i]) { indegrees[i]--; if (indegrees[i] == 0 ) { queue [tail++] = i; } } } } for (int i = 0 ; i < 26 ; i++) { if (edges[i]) { free (edges[i]); } } free (queue ); if (!valid || pos != edgesSize) { order[0 ] = '\0' ; } return order; }
[sol2-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 var alienOrder = function (words ) { let valid = true ; const edges = new Map (); const indegrees = new Map (); const length = words.length ; for (const word of words) { const wordLength = word.length ; for (let j = 0 ; j < wordLength; j++) { const c = word[j]; if (!edges.has (c)) { edges.set (c, []); } } } const addEdge = (before, after ) => { const length1 = before.length , length2 = after.length ; const length = Math .min (length1, length2); let index = 0 ; while (index < length) { const c1 = before[index], c2 = after[index]; if (c1 !== c2) { edges.get (c1).push (c2); indegrees.set (c2, (indegrees.get (c2) || 0 ) + 1 ); break ; } index++; } if (index === length && length1 > length2) { valid = false ; } } for (let i = 1 ; i < length && valid; i++) { addEdge (words[i - 1 ], words[i]); } if (!valid) { return "" ; } const queue = []; const letterSet = edges.keys (); for (const u of letterSet) { if (!indegrees.has (u)) { queue.push (u); } } const order = []; while (queue.length ) { const u = queue.shift (); order.push (u); const adjacent = edges.get (u); for (const v of adjacent) { indegrees.set (v, indegrees.get (v) - 1 ); if (indegrees.get (v) === 0 ) { queue.push (v); } } } return order.length === edges.size ? order.join ('' ) : "" ; };
[sol2-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 func alienOrder (words []string ) string { g := map [byte ][]byte {} inDeg := map [byte ]int {} for _, c := range words[0 ] { inDeg[byte (c)] = 0 } next: for i := 1 ; i < len (words); i++ { s, t := words[i-1 ], words[i] for _, c := range t { inDeg[byte (c)] += 0 } for j := 0 ; j < len (s) && j < len (t); j++ { if s[j] != t[j] { g[s[j]] = append (g[s[j]], t[j]) inDeg[t[j]]++ continue next } } if len (s) > len (t) { return "" } } order := make ([]byte , len (inDeg)) q := order[:0 ] for u, d := range inDeg { if d == 0 { q = append (q, u) } } for len (q) > 0 { u := q[0 ] q = q[1 :] for _, v := range g[u] { if inDeg[v]--; inDeg[v] == 0 { q = append (q, v) } } } if cap (q) == 0 { return string (order) } return "" }
复杂度分析
时间复杂度:O(n \times L + |\Sigma|),其中 n 是数组 words 的长度,即字典中的单词数,L 是字典中的平均单词长度,\Sigma 是字典中的字母集合。遍历字典构造有向图需要 O(n \times L) 的时间,由于有向图包含最多 n - 1 条边和 |\Sigma| 个节点,因此广度优先搜索需要 O(n + |\Sigma|) 的时间,总时间复杂度是 O(n \times L + n + |\Sigma|) = O(n \times L + |\Sigma|)。
空间复杂度:O(n + |\Sigma|),其中 n 是数组 words 的长度,即字典中的单词数,\Sigma 是字典中的字母集合。空间复杂度主要取决于存储有向图需要的空间,有向图包含最多 n - 1 条边和 |\Sigma| 个节点。